IEEE 754 표준 부동소수점 수의 형식, 부동소수점 산술연산

💎 IEEE 754 표준 부동소수점 수의 형식

• 지수 필드 : 바이어스 127 사용 (범위 : 128 ~ -127 )

• $1.M * 2^E$ 의 형태를 가지며, 소수점 아래의 M부분만 가수 필드에 저장

• [ 1S ][ 8E ] [ 23M ] 프레임을 가진다.

💍 표현 범위

• Zero : 0 00000000 00000000000000000000000
  전체가 0은 0이다.

• Normalized valued : [ S ] [1 to $2^9-2$] [ sigificand = 1.M ]
  기본적인 표현 방법으로 지수 표현 부가 -126 ~ 127 까지 이다.

• Infinity : [ S ] [ 11111111 ] [ 00000000000000000000000 ]
  지수 표현부가 128 이고, 가수가 0이다.
  ex) $\frac{1.0}{0.0}=\frac{-1.0}{-0.0}=\infin, \frac{1.0}{-0.0}=-\infin$

• NaN : [ S ] [ 11111111 ] [ non-zero ]
  지수 표현 부분이 128이고, 가수가 0이 아닌 다른 수이다.
  ex) sqrt(-1) , $\infin - \infin$, $\infin * 0$

• Denormalized valued : [ S ][ 00000000 ][ significand=0.M ]
  Normalized valued가 표현 할 수 있는 수보다 더 작은 수로, -126 지수를 가지고 있고,
  가수 부분의 일의자리 부분은, 0이다. M이 0이 아니어야 한다.
  가장 작은 가수는 0.000...1 이다.

💎 부동 소수점 산술 연산

💍 덧셈과 뺄셈

• 파이프라이닝
  1단계) 지수들이 일치되도록 조정한다.
  2단계) 가수들 간의 연산(더하기 혹은 빼기) 수행
  3단계) 결과를 정규화(normalization)

• ex) $(135 * 10^{-5} + (246 * 10^{-3} )$

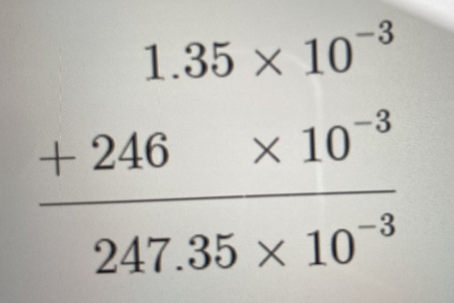
• FP ADD의 수학적 속성
  1) 모든 연산 결과에 대해서 답이 나온다. 값을 초과하면 무한대나, NaN이 나온다.
  2) 교환법칙 성립
  3) 결합법칙 불가 ex) $(3.14+1e10)-1e10 = 0, 3.14+(1e10-1e10) = 3.14$
  4) 모든 값에 0을 더하면 값이 같다.
  5) 모든 요소는 역수가 존재한다. 무한대와 NaN을 제외하고 ex) -2, +2
  6) 부등식에서 어떤 수를 더해도 그 부등식이 유지 된다. 무한대와 NaN을 제외하고
  ex) a >= b / a+c>=b+c

💍 부동소수점 곱셈 / 나눗셈

• 2진수 부동 소수점 곱셈 과정
  1) 가수들을 곱한다
  2) 지수들을 더한다
  3) 결과값을 정규화한다.

• 2진수 부동소수점 나눗셈 과정
  1) 가수들을 나눈다
  2) 피제수의 지수에서 제수의 지수를 뺀다
  3) 결과값을 정규화 한다.

• ex)

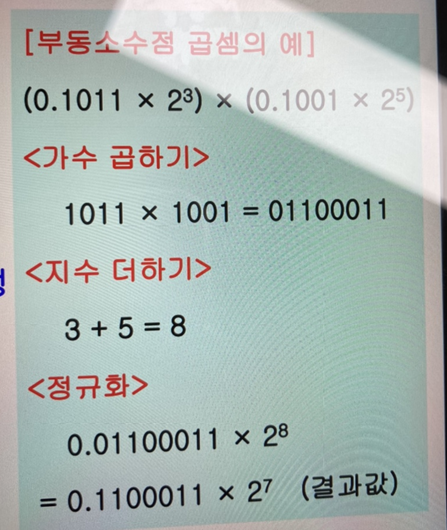
• FP Mult의 수학적 속성
  1) 모든 연산에 대한 값이 존재
  2) 교환법칙 성립
  3) 결합법칙 불가 ex) $(1e20*1e20)*1e{-20}=\infin, 1e20*(1e20*1e{-20})=1e20$
  4) 모든 수에 1을 곱하면 값이 같다.
  5) 분배법칙이 불가
  ex) $1e20*(1e20-1e20)=0.0, 1e20*1e20 -1e20*1e20 = NaN$
  6) 어떤 수를 곱해도 부등식이 성립한다. 무한대와 NaN을 제외하고
  ex) a>=b & c>=0 / a*c>=b*c

💍 부동 소수점 연산 과정에서 발생 가능한 문제점

• 지수 오버플로우 : $\infin, -\infin$ 으로 치환 / 양의 지수값이 최대 지수 값을 초과

• 지수 언더플로우 : 0으로 치환 / 음의 지수값이 최대 지수값을 초과

• 가수 언더플로우 : 두 수를 연산 했는데 가수 부분이 칸을 오른쪽으로 뚫고나감
  -반올림 해주어야 함
  -근데 만약에 예를 들어 칸이 두칸이고 0.795 라는 수가 있다고 하면 이 경우에는 0.80로 올림 한다. 이는 같은데 만약에 0.785 라는 수가 있다면 이 경우에는 0.78로 버림 한다. 그 이유는 딱 정중앙인 수인 5를 반올림 할 때 올림만 해주면 누적 될 시에 값이 크게 달라질 수 있기 때문이다. 이것의 반올림 할 때의 수가 짝수인 쪽으로 한다.

• 가수 오버플로우 : 같은 부호를 가진 두가수들을 덧셈하였을 때 올림수가 발생
  -재조정 과정을 통하여 정규화