다리를 지나는 트럭

원래벌레·2022년 11월 14일

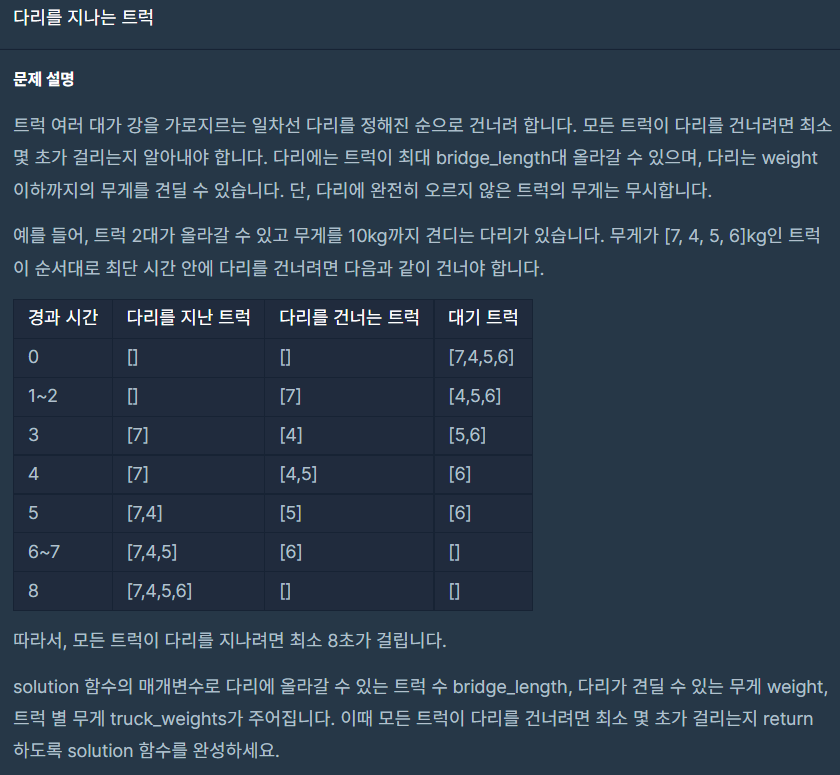
문제

문제의 시간 복잡도

n의 값이 10000 이하이다. 10000을 제곱하면 1억이다. CPU가 보통 1초에 1억개의 연산을 하기 때문에 시간 복잡도가 $O(n^2)$ 이하의 알고리즘을 사용하면 될 것이다.

문제에서 구해야 하는 답은 뭘까요?

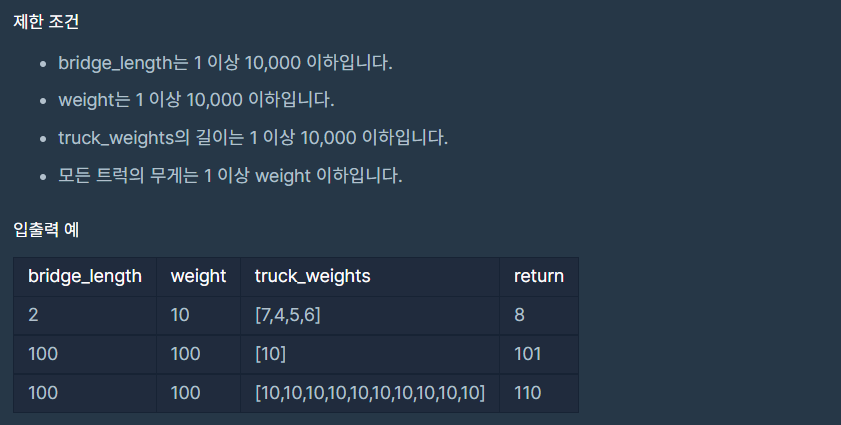
return 해야 하는 값은 트럭이 강을 지나가는데에 걸리는 최소시간이다. 여기서 변수들을 하나하나 살펴보면 먼저 bridge_length는 다리에 트럭이 올라 올 수 있는 숫자이다. weight는 다리가 감당 할 수 있는 트럭의 무게이다. 여기서 트럭의 무게는 완전히 올라오지 않은 트럭에 대해서는 값을 무시한다. truck_weights는 현재 대기중인 트럭들의 무게의 리스트이다.
현재 트럭들은 리스트에 정해진 순서대로 건너려고 하고 있다.

트럭은 총 네가지 상태를 가지고 있다.
1) 다리에 밖에서 기다리고 있는 상태
2) 다리에 완전히 올라간 상태
3) 다리에 완전히 올라가서 length = 1 만큼 이동한 상태
4) 다리를 건너간 상태

해당 상태에서 다음 상태로 넘어가기 위해서는 1초의 시간이 필요하다.

문제의 접근 방법

트럭의 경우 위의 네가지 상태를 가진다. 그래서 위의 네가지 상태를 구분을 할 수 있어야 한다고 먼저 생각을 했다.

대기 중인 트럭을 저장하는 큐, 다리 위에 올라가 있는 상태의 트럭을 저장하는 큐가 필요하다고 생각을 하였다.

그리고 다음 처리를 해야 할 것이 트럭이 다리에서 내려오는 경우라고 생각을 했다.

그리고 이에따라 필요한 변수들은 그때 그때 생각하면서 작성을 해주었다.

풀이

#include <string>
#include <vector>
#include <deque>
#include <iostream>

using namespace std;

int solution(int bridge_length, int weight, vector<int> truck_weights) {
    int answer = 0;    
    
    deque<int> t_weights;
    for(int i=0; i<truck_weights.size() ;i++)
    {
        t_weights.push_back(truck_weights[i]);
    }
    
    deque<pair<int,int> > OnTruck;
    
    int b_length=bridge_length;
    int b_weight=weight;
    
    int enter;
    
    while(t_weights.empty()==0 || OnTruck.empty()==0)
    {
        answer++;
        enter = t_weights[0];
        //다리에서 내려 갈 애가 있는지 본다.
        if(OnTruck.empty()==0)
        {
            if(OnTruck[0].first == bridge_length)
            {
                b_weight += OnTruck[0].second;
                b_length++;
                OnTruck.pop_front();
            }
            
            for(int i=0; i<OnTruck.size() ; i++)
            {
                OnTruck[i].first++;
            }
        }
        
        //트럭이 다리에 올라 올 수 있는 경우
        if(t_weights.empty()==0 && b_weight >= enter && bridge_length > 0)
        {
            OnTruck.push_back(make_pair(1,enter));
            t_weights.pop_front();
            b_weight = b_weight - enter;
            b_length--;
        }
        
    }
    
    return answer;
}

풀이의 시간복잡도

시간 복잡도의 영향을 주는 부분은 while문 내부이다.
결론적으로 bridge_length 값과 Truck의 갯수의 의해서 시간복잡도가 결정이 되는 것같다.
시간 복잡도의 값은 $bridge\_length * Truck + C$ 즉 $O(n*m)$ 이라고 생각을한다.