섬연결하기

---

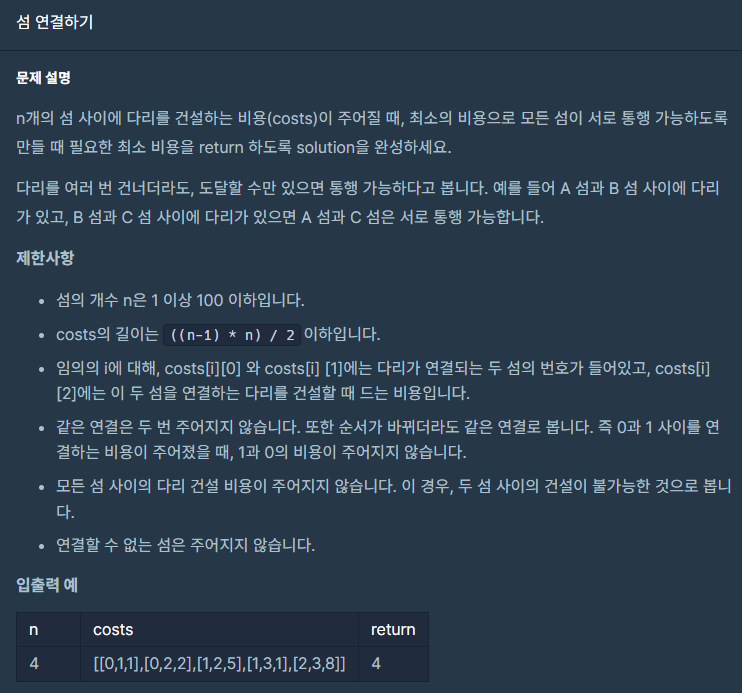
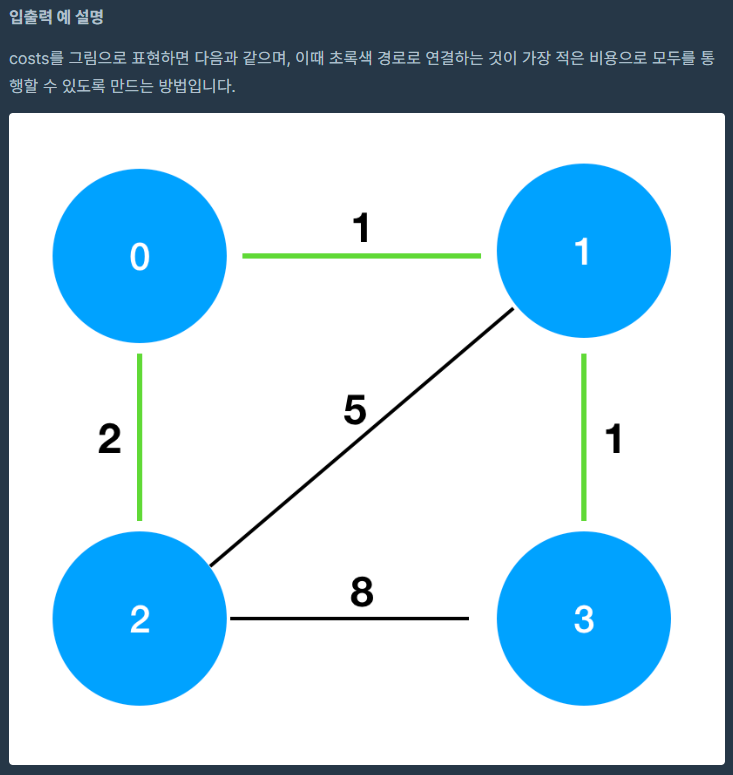
문제

---

풀이 (다른 사람의 풀이)

#include <string>
#include <vector>
#include <algorithm>
using namespace std;
int d[101];

int getParent(int node){
    if(node == d[node]){
        return node;
    }
    else return d[node] = getParent(d[node]);
}

bool compare(vector<int> a, vector<int> b){
    return a[2] < b[2];
}

int solution(int n, vector<vector<int>> costs) {

    int answer = 0;
    for(int i =0; i<n; i++){
        d[i] = i;
    }
    sort(costs.begin(), costs.end(), compare);
    for(int i=0; i<costs.size(); i++){
        int start = getParent(costs[i][0]);
        int end = getParent(costs[i][1]);
        int cost = costs[i][2];

        if(start != end){
            d[end] = start;

            answer += cost;
        }
    }


    return answer;
}

문제의 답을 확인하고 그 문제에 대한 설명을 적겠다.

일단 이 풀이의 경우에는 크루스칼 알고리즘을 사용했다.

크루스칼 알고리즘이란

최소신장트리를 구하는 알고리즘이다.

여기서 신장트리란 모든 노드들이 연결되어 있으면서 간선이 n-1개인 트리를 말한다.

그리고 이경우들 중에서 간선의 비용합이 가장 낮은 것이 최소신장트리이다.

그래서 이 최소신장트리를 어떻게 구하는가? 바로 크루스칼 알고리즘이 이것을 구하는 방법이다.

1) 간선을 비용을 기준으로 내림차순으로 정렬한다.
2) 앞쪽 인덱스의 간선을 하나씩 그리면서 사이클이 생기는지를 판별한다.
3) 사이클이 생기지 않았다면 간선으로 채택을 하고, 사이클이 생겨나면 채탁하지 않는다.
4) 이렇게해서 총 n-1개의 간선을 찾는다.

그렇다면 위의 풀이에서는 어떻게해서 사이클을 확인을 해주었는가?

1) 자기 자신을 부모노드로 갖는 노드들을 만들어준다.
2) 간선을 하나씩 확인하면서 cost의 0번과 1번 인덱스의 해당하는 노드의 부모노드를 각각 start와 end에 저장한다.
3) 이 start와 end의 값이 같지 않을 때, 즉 이 경우가 사이클이 생기지 않는 경우이다. 이를 간선중 하나로 채택을 하고 결과값을 증가시켜준다. 그리고 해당 인덱스 노드의 부모노드를 갱신해준다.

---

참고

출처 : https://chanhuiseok.github.io/posts/algo-33/