문제 풀러 가기

약수의 합 (Lv.1)

---

문제

정수 n을 입력받아 n의 약수를 모두 더한 값을 리턴하는 함수, solution을 완성해주세요.

제한 사항

• n은 0 이상 3000이하인 정수입니다.

입출력 예

n	return
12	28
5	6

입출력 예 설명

입출력 예 #1
12의 약수는 1, 2, 3, 4, 6, 12입니다. 이를 모두 더하면 28입니다.

입출력 예 #2
5의 약수는 1, 5입니다. 이를 모두 더하면 6입니다.

---

나의 풀이

풀이 (1)

function solution(num) {
  const arr = [];
  for (let i = 0; i <= num; i++) {
    if (num % i === 0) arr.push(i);
  }
  return arr.reduce((a, c) => a + c, 0);
}

• input을 나누었을때 나머지가 0인 정수를 모조리 찾으면 된다
• 모든 숫자를 배열에 넣어 누산 후 합계를 반환한다
• 하지만 0부터 input까지 숫자를 1씩 더해가며 계산해야하므로 시간 복잡도가 상당하다 (+4점)

풀이 (2) : 다른 시도 (미제출)

function findDivisor2(num, count = 0) {
  const arr = [];
  for (let i = 1; i <= num; i++) {
    if (num % i === 0) arr.push(i);
    count++;
  }
  return `${arr.sort((a, b) => a - b)}\ncount: ${count}`;
}

console.log(findDivisor2(12));
console.log(findDivisor2(72));
console.log(findDivisor2(360));

console.log(`-------------------------------------------`);

function findDivisor(num, count = 0) {
  const arr = [];
  for (let i = 1; i * i <= num; i++) {
    if (num % i === 0) arr.push(i, num / i);
    count++;
  }
  return `${arr.sort((a, b) => a - b)}\ncount: ${count}`;
}

console.log(findDivisor(12));
console.log(findDivisor(72));
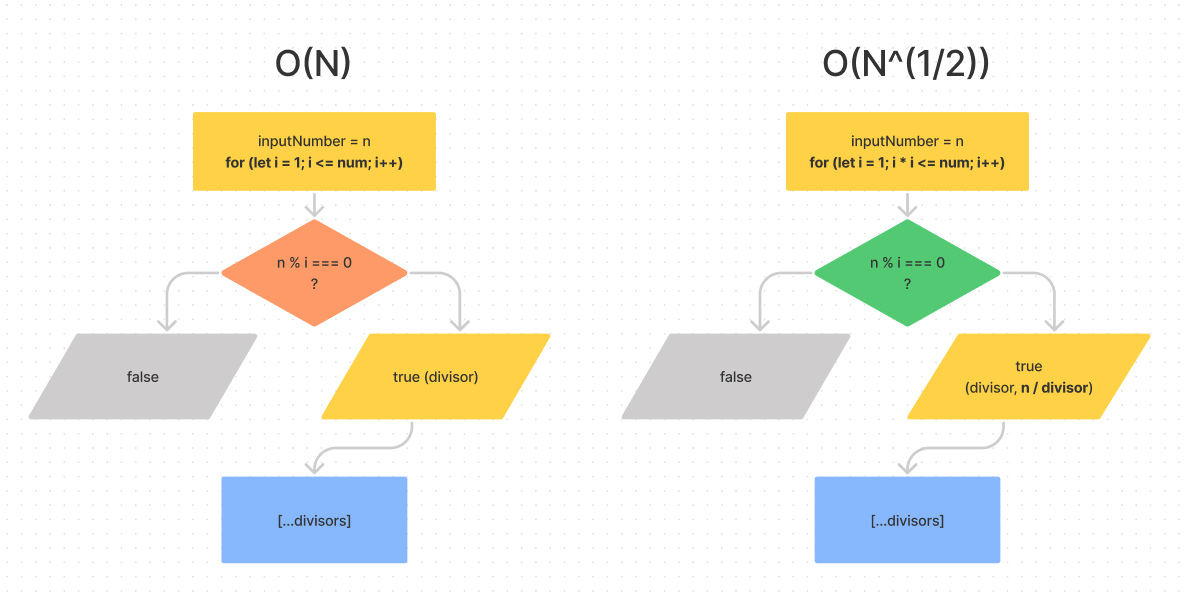
console.log(findDivisor(360));

중앙의 하이픈(---)을 기준으로 위는 하나 하나 숫자를 더해가며 계산하는 코드, 아래는 '임의의 자연수 N의 약수들 중에서 두 약수의 곱이 N이 되는 약수 A와 약수 B는 반드시 존재한다'는 명제를 활용하여 i의 제곱까지만 구하고, 결과로 n/i를 추가한 코드다.

위 코드는 n번만큼 연산을 수행하지만, 아래 코드는 훨씬 더 적은 연산으로 같은 결과를 도출한다. 따라서 아래 코드를 사용하면 리소스 사용을 줄일 수 있겠다.
수학적 연산의 원리를 이해한 것은 아니고, 계산을 간단히 하는 명제와 도식을 찾아와 코드로 바꾼 것이지만, 모든것을 완전히 이해할 필요는 없을 것 같다. 구글이 언제나 함께하니까

---

다른 사람의 풀이

다른 풀이 (1)

function solution(n, a=0, b=0) {
    return n<=a/2?b:solution(n,a+1,b+=n%a?0:a);
}

봐도 잘 모르겠다

다른 풀이 (2)

function solution(num) {
    let sum = 0;
    for (let i = 1; i <= num; i++) {
        if (num % i === 0) sum += i
    }
    return sum
}

나의 풀이와 마찬가지로 하나씩 숫자를 더해가며 찾는 풀이