[ML] Logistic Regression MNIST Classification 구현

숫자 0~9까지의 손글씨 이미지와 이미지의 label(0~9)로 되어있는 train data와 test data를 MNIST data라고 한다. MNIST data를 이용하여 Logistic Regression으로 multiple classification을 수행하기.

KNN MNIST Classification도 과제로 했지만, KNN은 IRIS Classification과 코드가 거의 비슷하여 첨부하지 않았다.

Losigtic Regression

이벤트가 발생할 확률을 결정하는 데 사용되는 통계 모델. 특성 간의
관계를 보여주고 특정 결과의 확률을 계산함. 선형회귀(Linear Regression)과 비슷하며 값이 이진(1 또는 0)으로 나옴.

✔ sigmoid : cost 계산 및 class 예측에 사용

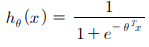
✔ cost function : θ를 이용하여 오차(cost) 계산, 데이터(60000개)에 대한 평균을 계산, 확률을 제대로 예측하는지 평가하는 지표

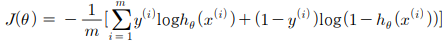
✔ gradient descent : cost function의 기울기(미분값)을 계산하여 θ가 최솟값을 가지게 변화시킴

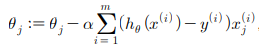
이 세 개의 함수들을 이용하여 Logistic Regression을 구현하여 MNIST Classfication을 할 수 있다.

Logistic_regression_class.py

x_train : 60000x785 (784(28x28)+1(bias와 계산), 이미지 파일을 1차원 배열로 저장)
t_train : 60000x10 (one hot lable로 변경)
θ : 785x10 (θ0에 bias 삽입)

import numpy as np
import sys, os
import numpy as np
# from PIL import Image
sys.path.append(os.pardir)
from dataset.mnist import load_mnist

class LogisticRegression:
    def __init__(self, x, y):
        # t_train(training data의 index)를 one hot encoding된 배열(60000x10)로 받기 위해 one_hot_label=True로 설정
        (self.x_train, self.t_train), (self.x_test, self.t_test) = load_mnist(flatten=True, normalize=False, one_hot_label=True)
        self.x_train = np.insert(self.x_train, 0, 1, axis=1)  # theta0를 bias로 하여 계산하기 위해 training data의 첫번째 열에 1 추가
        self.x_train = self.x_train.astype(np.int64)  # overflow 방지를 위해 type 변환

        self.m = np.shape(self.x_train)[0] # m : data의 수(60000)
        self.n = np.shape(self.x_train)[1] # n : feature의 수(785)

        # 최초의 theta는 0행렬(785x10)
        # theta0를 bias값으로 사용
        self.theta = np.zeros((self.n, 10))

    # h(theta)
    def sigmoid(self, x, theta):
        return 1.0 / (1.0 + np.exp(-np.dot(x, theta))) 

    # J(theta)
    def cost(self, x, y, theta): #1x10
        delta = 1e-7 # 무한대 방지를 위해 log에 더해줄 값

        hx = self.sigmoid(x, theta) 
        cost_arr = y * np.log(hx + delta) + (1-y) * np.log(1-hx + delta)
        return (-1/self.m) * (np.sum(cost_arr, axis=0))

    # gradient descent를 이용하여 theta의 최솟값 구하기
    def learn(self, rate, epoch):
        # 입력받은 epoch만큼 반복하여 theta 계산(update)
        for e in range(epoch):
            # class별(coloumn별)로 계산
            for i in range(10):   
                dt = (self.sigmoid(self.x_train, self.theta[:, i]) - self.t_train[:, i]).reshape(self.m, 1) * self.x_train
                self.theta[:, i] = self.theta[:, i] - rate * np.sum(dt, axis=0)
            print('epoch: ', e, 'cost: ', self.cost(self.x_train, self.t_train, self.theta))

        # 예측 과정에 학습 완료된 theta값이 필요하므로 theta return    
        return self.theta

    # test_data의 class 예측
    # 모든 클래스에 대해 계산하고, sigmoid 값이 가장 큰 class를 return
    def predict(self, x, theta):
        result = self.sigmoid(x.reshape(1, np.shape(x)[0]), theta)
        return np.argmax(result)

cost()

log 내부에 delta를 더하는 이유 : log를 취한 값이 0이 되어 무한대로 발산하는 것을 막기 위함

main.py

60000개의 train data를 이용하여 학습시켜 최적의 θ값을 알아낸 후 정확도 측정

import numpy as np
import logistic_regression_class as lg
import sys, os
sys.path.append(os.pardir)
from dataset.mnist import load_mnist

(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)

# theta에 bias가 추가되어있으므로(785x10) test data에도 bias 연산에 필요한 1을 삽입(10000x785)
x_test = np.insert(x_test, 0, 1, axis=1)
x_test = x_test.astype(np.int64)

# 학습을 통해 theta값을 구함
lgr = lg.LogisticRegression(x_train, t_train)
theta = lgr.learn(0.00001, 400)

sum = 0.0
for i in range(0, 100):
    print(i, ' predict: ', lgr.predict(x_test[i], theta), ' real: ', t_test[i])
    if lgr.predict(x_test[i], theta) == t_test[i]:
        sum += 1.0
print('accuracy: ', sum/100.0)