오늘의 문제
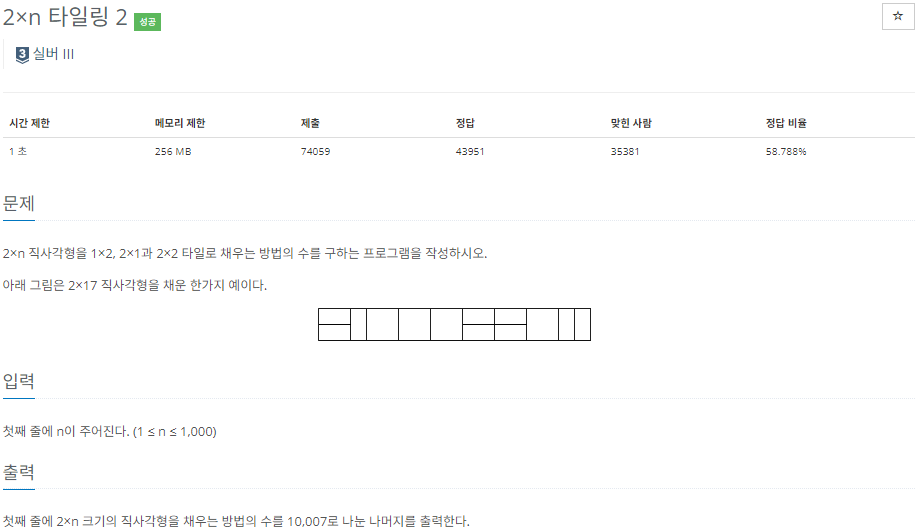
11727 2×n 타일링 2
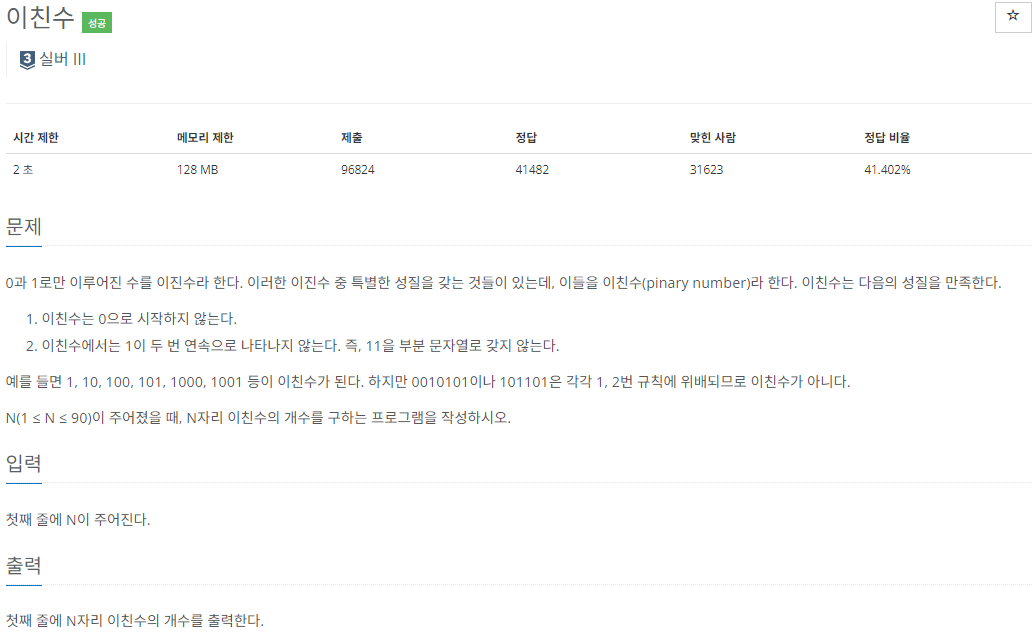
2193 이친수
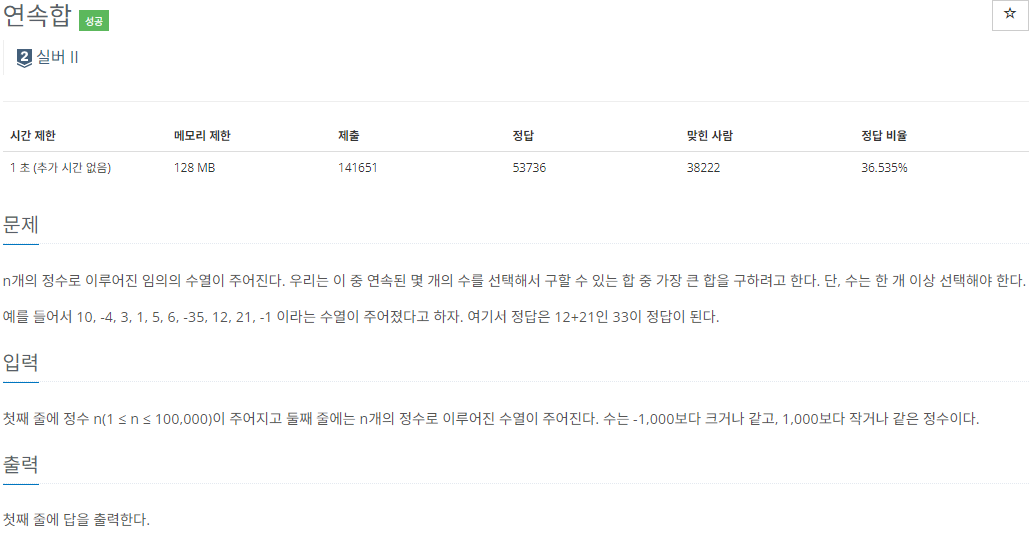
1912 연속합
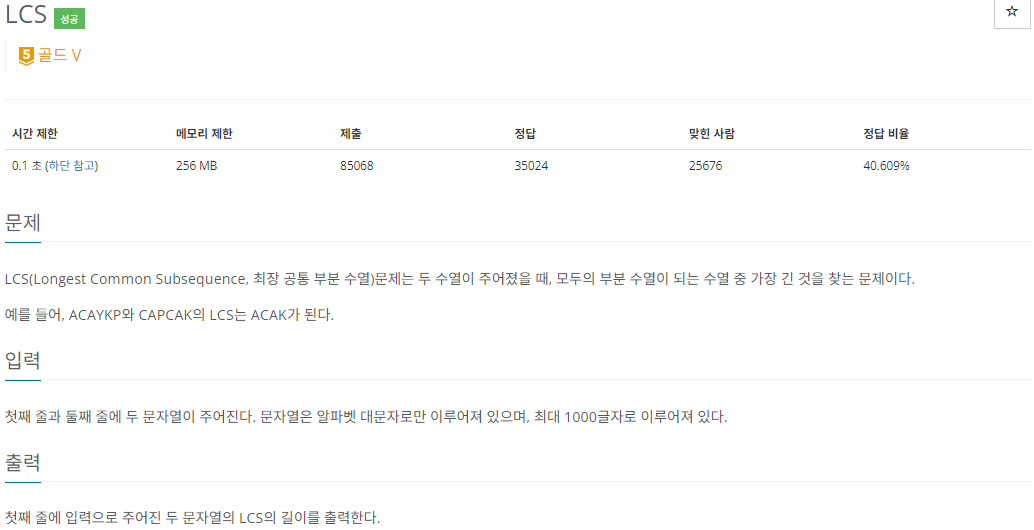
9251 LCS
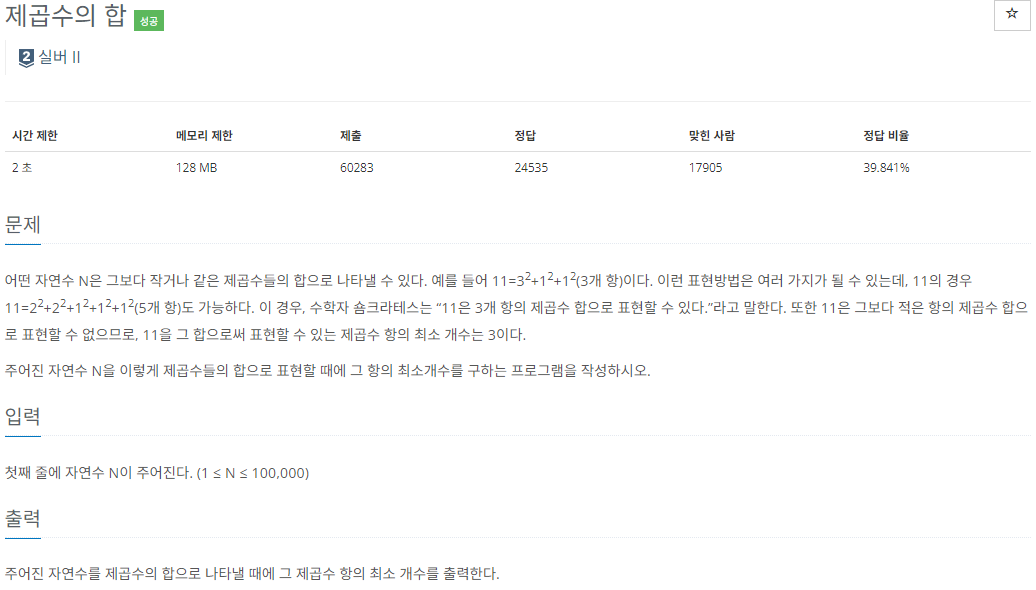
1699 제곱수의 합

11727 2×n 타일링 2

코드

#include <bits/stdc++.h>
using namespace std;

int n, dp[1002];

int main() {
	cin >> n;
	dp[1] = 1;
	dp[2] = 3;
	for (int i = 3; i <= n; i++) {
		dp[i] = (dp[i - 1] + dp[i - 2] * 2 )% 10007;
	}

	cout << dp[n];
}

2193 이친수

코드

#include <bits/stdc++.h>
using namespace std;

long long n, dp[100];

int main() {
	cin >> n;
	dp[1] = 1;

	for (int i = 2; i <= n; i++) {
		dp[i] = dp[i - 1] + dp[i - 2];
	}
	cout << dp[n];
}

늘 자료형에 주의하기

1912 연속합

코드

#include <bits/stdc++.h>
using namespace std;

int n, num[100002], dp[100002];

int main() {
	cin >> n;
	for (int i = 0; i < n; i++) cin >> num[i];

	dp[0] = num[0];
	for (int i = 1; i < n; i++) {
		dp[i] = max(dp[i - 1] + num[i], num[i]);
	}
	int ans = -200000000;
	for (int i = 0; i < n; i++) ans = max(dp[i], ans);
	cout << ans;
}

9251 LCS

코드

#include <bits/stdc++.h>
using namespace std;

string s1, s2;
int dp[1002][1002];

int main() {
	cin >> s1 >> s2;
	
	int len1 = s1.size(), len2 = s2.size();
	for (int i = 1; i <= len1; i++) {
		for (int j = 1; j <= len2; j++) {
			if (s1[i - 1] == s2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
			else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
		}
	}
	cout << dp[len1][len2];
}

1699 제곱수의 합

코드

#include <bits/stdc++.h>
using namespace std;

int n, dp[100002];

int main() {
	cin >> n;
	
	for (int i = 1; i <= n; i++) {
		dp[i] = i;
		for (int j = 1; j * j <= i; j++) {
			dp[i] = min(dp[i], dp[i - j * j] + 1);
		}
	}
	cout << dp[n];
}