2630 색종이 만들기

아이디어

분할 정복 문제 중 직관적인 편에 속했다고 생각하는 문제.
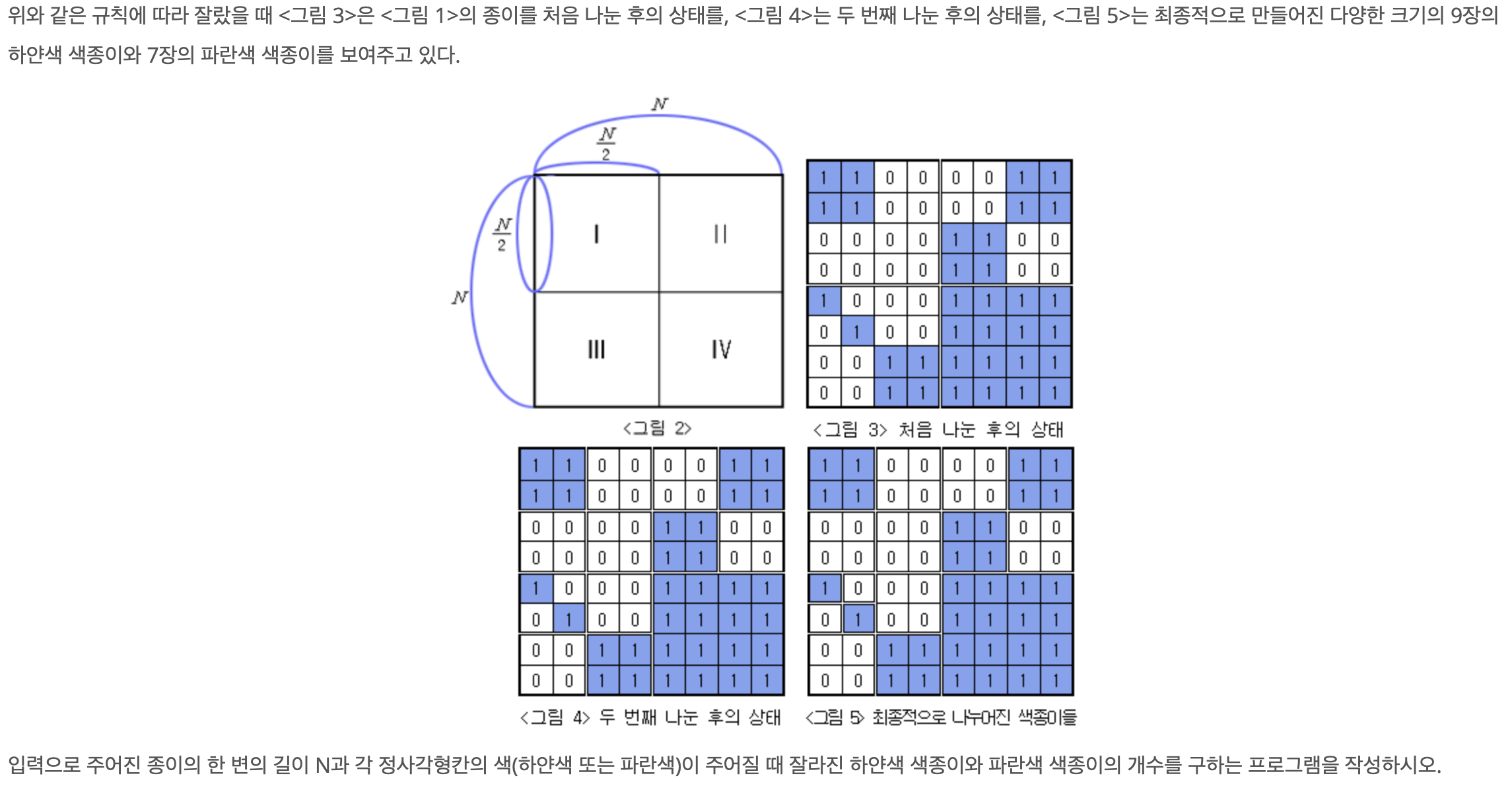
재귀함수의 기저조건이 그림에 드러나 있었다.
(자른 종이가 모두 파란색이거나, 모두 흰색이거나)
size*size 형태의 행렬이 0 또는 1로만 이루어져 있을 때 재귀 종료,
그렇지 않을 땐 4등분하여 각각 재귀함수 호출.

구현

제출 (재귀 이용, 정답)

import sys

input = sys.stdin.readline

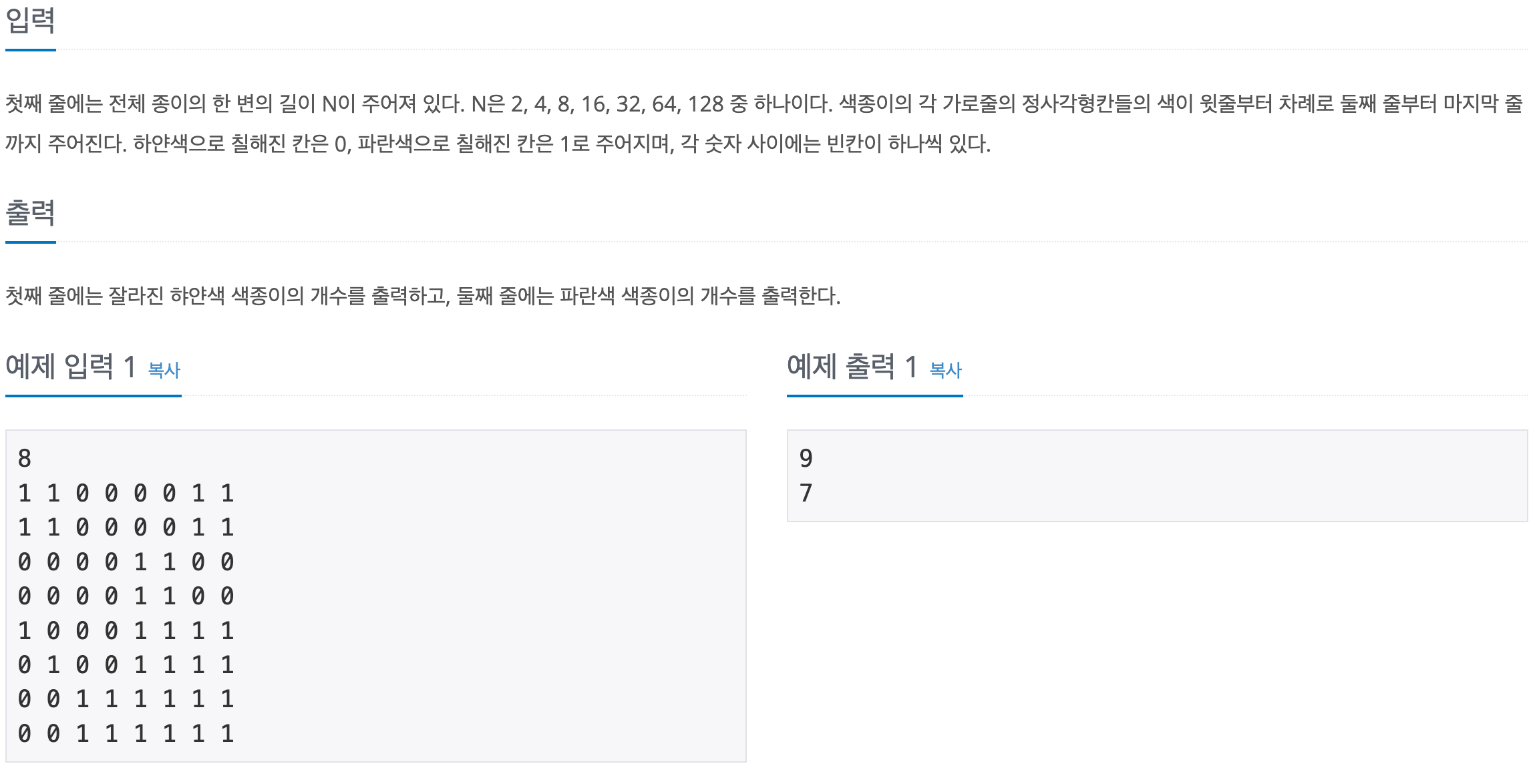
n = int(input())
whole_paper = [input().split() for _ in range(n)]
white = 0
blue = 0


def cutting(paper, size, min, max):  # i가 행, j가 열
    global white
    global blue
    if paper == [["0"] * size] * size:
        white += 1
        return
    elif paper == [["1"] * size] * size:
        blue += 1
        return
    else:
        mid = (min + max) // 2

        quarter_1 = [paper[i][min:mid] for i in range(min, mid)]
        quarter_2 = [paper[i][mid:max] for i in range(min, mid)]
        quarter_3 = [paper[i][min:mid] for i in range(mid, max)]
        quarter_4 = [paper[i][mid:max] for i in range(mid, max)]

        cutting(quarter_1, size // 2, 0, mid)  # 1사분면 (왼쪽 위)
        cutting(quarter_2, size // 2, 0, mid)  # 2사분면 (오른쪽 위)
        cutting(quarter_3, size // 2, 0, mid)  # 3사분면 (왼쪽 아래)
        cutting(quarter_4, size // 2, 0, mid)  # 4사분면 (오른쪽 아래)
        return


cutting(whole_paper, n, 0, n)
print(white)
print(blue)

Z 문제에서 "사분면을 나눈 후에도 인덱스 번호를 유지해야 한다"라는 조건이 있었던 게 생각나서 이번에도 인덱스 번호를 유지하게 하려다가 한참 시간을 썼다.
그러다가 깨달았다. 이번에는 인덱스를 유지할 필요가 없다는 것을...