9050 골드바흐의 추측

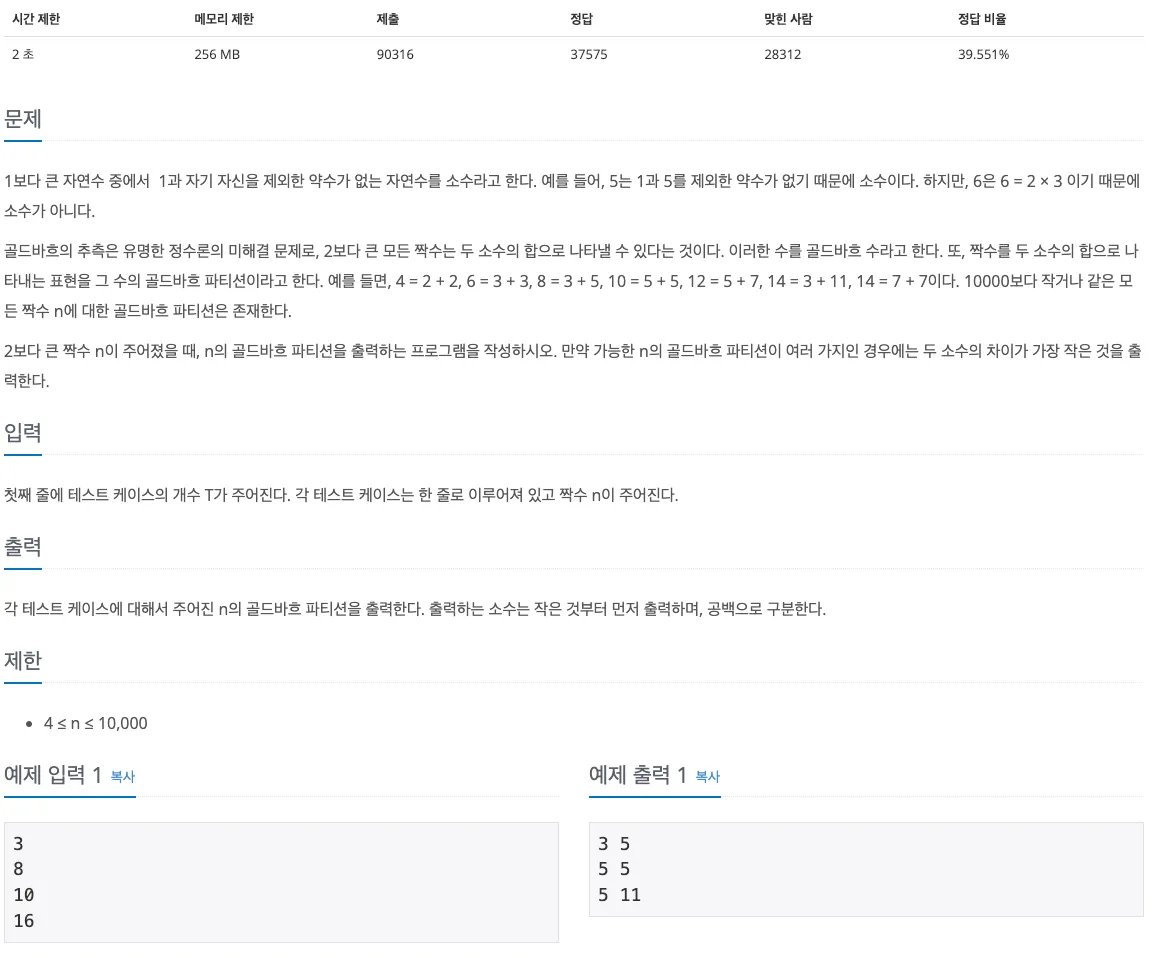
아이디어 도출

일단 주어지는 수보다 작은 소수 리스트가 반드시 필요 -> 그래서 소수 찾기 문제와 연동.

그 다음에, 골드바흐 파티션의 특성 -> 무조건 n//2 +- i의 형태를 띤다는 것 이용.
i=0일 때부터 찾기 시작해서 n//2 + i, n//2 - i가 둘 다 소수일 때 종료하고 두 값을 반환.

구현

시간 초과와의 전쟁.

제출 1 (시간 초과)

def prime_checker(number):
    if number == 1:
        return False
    else:
        for i in range(2, number):  # 2부터 자기 자신-1 까지 나머지가 0이 나오면 제외
            if number % i == 0:
                return False
        return True


def prime_list_maker(n):
    numbers = list(range(2, n))
    return [number for number in numbers if prime_checker(number)]


n = int(input())
for _ in range(n):
    num = int(input())
    prime_list = prime_list_maker(num)
    for i in range(num // 2):
        if (num // 2) - i in prime_list and (num // 2) + i in prime_list:
            print(f"{(num//2)-i} {(num//2)+i}")
            break

왜 시간 초과인가? 구현된 로직을 살펴보면,

1. 일단 prime_checker라는 소수 판정 함수를 만듦
2. 어떤 수 n에 대해 n보다 작은 소수 리스트를 만드는 prime_list_maker라는 함수를 만듦
3. 이제 어떤 수 입력 하나가 들어올 때마다, prime_list_maker를 통해 소수 리스트를 만듦
4. 그 리스트에서 골드바흐 파티션을 찾는 로직 실행

그러나.. 이럴 경우에 문제가 되는 것은,

시간복잡도!!!

제출 2 (정답)

import math

def prime_list_maker(number):
    prime_list = [2]
    for i in range(3, number, 2):
        for prime in prime_list:
            if i % prime == 0:
                break
        else:
            prime_list.append(i)  # for 문 뒤의 else..
    return prime_list

prime_list = prime_list_maker(10000)

n = int(input())
for _ in range(n):
    num = int(input())
    for i in range(num // 2):
        if (num // 2) - i in prime_list and (num // 2) + i in prime_list:
            print(f"{(num//2)-i} {(num//2)+i}")
            break

결국 미리 10000까지의 소수 리스트를 만들어 놓고, 그 안에서 조회하면 된다.. 그게 더 빠르다..
그러니까 "입력값이 작을 때는 소수가 몇 개 안되니까 그때그때 만들면 되지 않을까?"라는 발상은 위험할 수 있다!
함수 안에서 다른 함수를 실행하는 구조는 O(n^2)를 만들 확률이 높다!!