[C++] tree 구현(2)

탐색 기능

• 데이터 삽입이 복잡한 대신 탐색 시 간편함
• 탐색 기능 구현하기
  근데 구현하려면 반복자 필요함.

근데 이건 insert아닌가 왜 여기서 구현한겨
(수정)

• 지금 자체적으로 tPair 구조체 템플릿 만들어서 데이터 관리 시 페어라는 단위를 사용 중임.
  pair 객체를 직접 선언하고 값을 초기화해주는 게 번거롭기 때문에 make_pair 와 같은 기능을 하는 함수를 구현하도록 한다.
  
  

make_bstpair()

선언

• 반환 타입 : tPair (페어)
• tPair가 템플릿이므로 , 페어를 만들어주는 함수도 자연스럽게 템플릿이 된다.

template<typename T1, typename T2>
tPair<T1, T2> make_bstpair(const T1& _first, const T2& _second)
{
	return tPair<T1, T2>{_first, _second};
}

find()

iterator 클래스

반복자가 어떤 데이터를 받고 있어야, BST가 관리하는 노드의 데이터를 가리키는 역할을 할 수 있을까?? 뭘 알면 좋을까?
-> (어차피 페어 안에 키/값 데이터 들어있으니까) 가리키고 있는 노드를 알면 됨.

• end 개념을 만들어야 한다
  반복자가 가리키는 노드 포인터가 널일때 가 end임

• 단순히 노드 주소만 알고 있으면 뭐가 루트인지, 이런 정보를 반복자가 빠르게 알기 어렵다..
  -> 노드들을 관리하고 있는 BST한테 걍 루트 누구냐고 물어보는게 빠름
  => 따라서 반복자가 BST 본체도 알 수 있게 포인터변수로 가리킴

• begin iterator도 만들기

---

이전에 배운내용
(템플릿의??) 반환 타입이 본인 클래스 안에 있는 내부클래스일 경우, 반환타입 앞에 typename 적어줘야 함

• begin()
  BST에선 중위 순회가 중요, 따라서 중위 순회 기준으로 첫 번째인 노드가 begin
  -> 어떻게 해야 그 중위순회의 첫번째 노드를 찾을 수 있을까??

begin 함수 자체가 BST 함수이므로, 본인 멤버 루트가 있을 것임
루트부터 시작해서 반복문 돌면서 노드의 왼쪽 자식이 없을 때까지 반복.
왼쪽 자식 있으면 현재 노드를 그 왼쪽 노드로 바꿈
왼쪽자식 노드가 null이면 반복문 탈출,
이 때의 노드가 바로 반복자가 가리키는 노드가 된다. 이거 반환함 ㅇㅇ

• end()
  end는 걍 널포인터 반환하면 됨

• find()
  (첫 번째 타입을 기준으로 찾으니까 T1 타입을 받아온다)
  찾는 과정이 insert할 때랑 굉장히 비슷함
  -> insert()의 코드를 일부 가져와서 수정한다.
  ->insert와 다르게 else에 걸리면(둘이 같으면) 찾은 거다. 찾았으니 break하고 현재 노드를 가리키는 반복자를 반환함
  ->nullptr면 못찾은 거임.
  
  

<연산자 함수>

==

bool operator ==(const iterator& _other)
{
	if (m_pBST == _other.m_pBST && m_pNode == _other.m_pNode)
		return true;
	return false;

!=

bool operator !=(const iterator& _other)
{
	return !(*this == _other);
}

*

역참조 연산자(*)로 접근하면, 반복자가 가리키고 있는 데이터에 접근한다는 건데
그 데이터는 2개가 묶여있는 페어다.
-> 반환타입이 페어
first가 키값인데 수정하면 안 되지 않을까?
-> 원본 참조로 반환은 하되 수정 못 하게 const로 줌

• 걍 현재 가리키는 노드의 페어 반환하면 됨.
• 근데 지금 end면 어떡함?
  end는 마지막의 다음을 가리키는데 거기 값을 꺼내는 게 불가능함.
  => 따라서 노드가 nullptr면 assert에 걸리게 해서 경고처리.

const tPair<T1, T2>& operator *()
{
	// m_pNode nullptr 체크(end iterator인지 아닌지)
	assert(m_pNode);

	return m_pNode->pair
}

• 다 만들면

(*iter).first;
(*iter).second;

-> 이런 식으로 tPair 구조체 멤버에 접근할 수 있다.

💡 아래의 -> 연산자 로 더 간편하게 접근이 가능하다

->

: 역참조 연산자(*)와 유사하나, 반환 타입이 &가 아닌 * 이며 현재 노드의 페어 주솟값를 반환한다.

const tPair<T1, T2>* operator ->()
{
	// m_pNode nullptr 체크(end iterator인지 아닌지)
	assert(m_pNode);
			
	return &m_pNode->pair
}

• 의문 ..
  페어 주소까지 접근했다 쳐도.
  다시 -> 를 해서 거기서 어떤 멤버로 접근할 지 알려줘야 하는 거 아닌가??

Iter->->second;

이렇게..
근데 그냥 저 화살표를 한 번 생략할 수 있게 만든거임

화살표 연산자의 리턴값이 주소인 경우에는 굳이 화살표 두 번 안 쓰고도 접근할 수 있게 함.

++

중위순회 : In-order
중위 선행자 : Inorder predecessor
중위 후속자 : Inorder Successor

• ++할 때 다음 데이터로 이동하는 기준 :중위순회
  -> 중위 순회 기준으로, 이전 데이터를 중위 선행자 / 다음 데이터를 중위 후속자 라고 한다.

• 반복자에서 ++ 기능이 필요한 거지만, BST 자체적으로 이 중위 후속자를 찾는 기능을 제공함
  -> 그럼 반복자 입장에선,
  현재 가리키는 노드의 중위 후속자를 BST한테 물어보면 되겠네.

중위 후속자

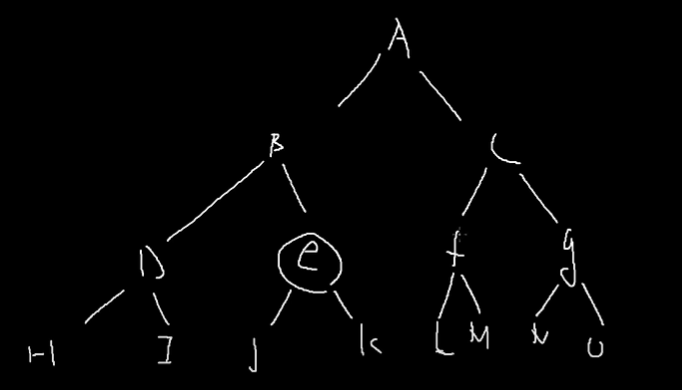
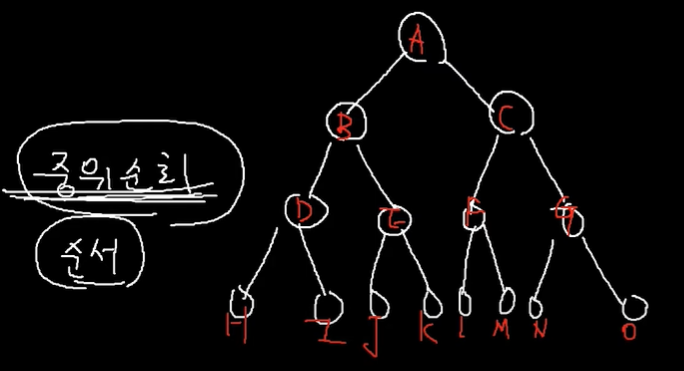
• H D I B J E K A L F M C N G O

H의 중위 후속자는 D
D의 중위 후속자는 I
I의 중위 후속자는 B
H는 D의 왼쪽 자식
D는 B의 왼쪽 자식
...

• 알고리즘

1. 오른쪽 자식이 있는 경우
   -> 오른쪽 자식으로 가서, 왼쪽 자식이 없을 때까지 왼쪽으로 가면 걔가 중위후속자
2. (1은 X), 본인이 왼쪽 자식인 경우
   -> 부모가 중위후속자
3. 본인이 오른쪽 자식일 경우 부모가 왼쪽 자식일 때까지 올라감
   -> 그 부모의 부모가 중위후속자

O의 경우 )
1. 오른쪽 자식 없음 : X
2. 본인 왼쪽 자식 아님 : X
3. 왼쪽 자식인 부모 없음 : X
-> end 노드

• 구현
  다른건 주석에 써놨고
  2번에 이거 너무 지저분함!!

//부모로 가서, 부모의 왼쪽 자식이 현재 노드와 같은지 비교
pSuccessor->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::LCHILD] == pSuccessor;

-> 노드 쪽에서 아예 함수를 지원하자.

IsLeftChild()

본인이 부모로부터 왼쪽 자식인지 확인하는 함수

만약 부모가 없는 경우는?
루트 노드한테 왼쪽 자식이냐고 물어보면 안 되지
-> 본인이 루트노드인지 체크할 수 있는 함수 만들기

IsRoot()

bool IsRoot()
{
	if (nullptr == arrNode[(int)NODE_TYPE::PARENT])
		return true;
	return false;
}

IsRightChild()

레프트 활용해서 만들기

중위 선행자

: 중위 후속자와 정확히 대칭구조임

• O G N C M F L A K E J B I D H

• 알고리즘

1. 왼쪽 자식이 있는 경우
   -> 왼쪽 자식으로 가서, 오른쪽 자식이 없을 때까지 오른쪽으로 가면 걔가 중위선행자
2. (1은 X), 본인이 오른쪽 자식인 경우
   -> 부모가 중위선행자
3. 본인이 왼쪽 자식인 경우 부모가 오른쪽 자식일 때까지 올라감
   -> 그 부모의 부모가 중위선행자

H의 경우 )
1. 왼쪽 자식 : X
2. 본인 오른쪽 자식 : X
3. 오른쪽 자식인 부모 : X
-> end 노드

erase()

• 트리 노드 냅다 삭제해 버리면 연결 관계에 문제가 생김
  그래서 삭제할 때도 다양한 케이스별로 구분하여 구현해야 한다.
  (어소트락 홈피
  https://assortrock.com/m/48)

• 삭제할 노드를 탐색한 뒤 3가지 경우로 나뉜다.

1. 삭제할 노드가 단말노드인 경우
2. 삭제할 노드가 자식노드를 한 개 가진 경우
3. 삭제할 노드가 2개의 자식을 가진 경우
   👉 1은 그냥 데이터 지우면 되고
   2는 자식이 삭제된 부모 자리 대체하면 됨

3은 고민 할 필요가 없음.
부모보다 오른쪽이 크고, 왼쪽이 작단 규칙을 잘 지켰을 경우
자식 둘 중 누구를 올릴지 고민할 게 아니라, 중위순회 순서에 문제가 없을지 고민해야 함

• H D I B J E K A L F M C N G O
  -> B 삭제할 경우, 자식인 D,E가 아니라
  중위 선행자/후속자인 I나 J가 대체해야 함

• 트리의 노드 삭제할 때, 실제 노드를 삭제하고 연결 관계를 다시 설정할 것이 아니라
  노드에 들어있는 데이터 파트를 복사하면 되지 않을까? (포인터 말고)

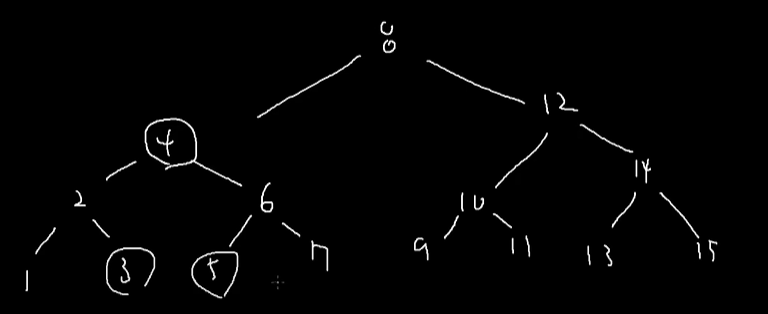
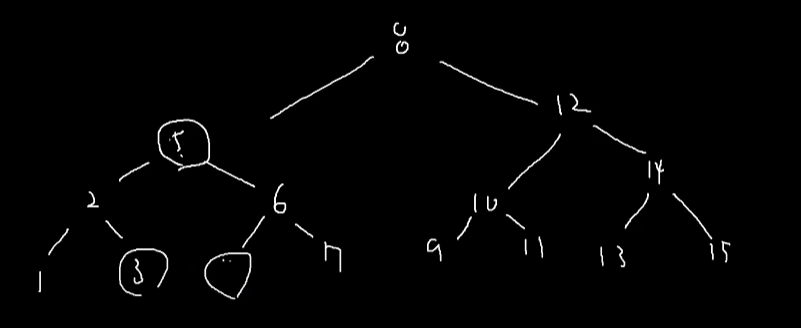
-> 삭제된 4 자리에 5의 데이터를 복사해도, 순서에 아무 문제X

• 근데 실질적으로 메모리상 삭제되는 중위 선행자/후속자 노드의 자식이 몇 개인지에 따라 또 케이스가 나뉨;;
  -> 근데 케이스 3을 고려할 필요가 없는게,
  애초에 중위 선행자/후속자면 자식이 2개일 수가 없음

• BST는 삭제 시, 다른 자료구조들과 마찬가지로 반복자를 사용한다.
  -> 삭제하고자 하는 노드를 가리키는 반복자를 받아서, 걔가 가리키는 노드를 지워줌

• 근데 erase 함수의 반환값은 어떤 의미였음??
  -> 지운 데이터의 그 다음 요소를 가리키는 반복자였음

• 그럼 여기서는, 지운 노드의 다음 요소라는 건 중위 후속자를 의미한다

---

구현

• 일단 예외처리 )
  애초에 해당 반복자가 우리 BST의 노드를 가리키는 게 맞는지 확인한다.
  -> BST 안에서 iterator의 private 멤버에접근할 수 없으므로 iterator 쪽에서 친구 선언을 해 준다.

assert(this == _iter.m_pBST);

• 반복자가 가리키는 노드가 자식이 몇 개인지 확인한다.
  👉 단말 노드인지, 텅 빈 노드인지 확인하는 함수 만들기

  • 노드 삭제해버리면 부모에게 접근할 수 없기 때문에, 삭제하기 전에 먼저 부모로 접근해서, 삭제할 자식의 방향에 따라 부모의 자식 가리키는 포인터 nullptr로 바꿔줘야 한다.

• 삭제 후 다음 노드를 가리키는 반복자를 반환해야 하는데. 이것까지 모두 erase 함수 안에서 다 수행하기엔 너무 복잡한 것 같다..

• 아니 다 써놧더니 또 코드를 바꾸자고 하네
  순수하게 특정 노드를 삭제한다는 기능을 만들어 놓고, erase에서 재호출하는 걸로 변경할 것
  -> 결국 erase는 반복자가 가리키는 노드를 제거해서, 그 노드의 중위 후속자를 가리키는 반복자를 만들어 반환해주는 함수가 된다

erase 함수

template<typename T1, typename T2>
inline typename CBST<T1,T2>::iterator CBST<T1, T2>::erase(const iterator& _iter)
{
	assert(this == _iter.m_pBST);

	tBSTNode<T1, T2>* pSuccessor = DeleteNode(_iter.m_pNode);

	return iterator(this, pSuccessor);
}

---

DeleteNode()

외부엔 공개 ㄴㄴ
선언

private:
	tBNSTNode<T1, T2>* DeleteNode(tBSTNode<T1, T2>* _pTargetNode);

• 자식이 하나도 없는 경우 / 2개인 경우 / 1개인 경우 를 나눠서 구현한다.
  • 자식이 하나도 없는 경우일 때, 삭제하려는 노드가 루트 노드일 경우를 예외처리한다.
    -> 만약 루트노트이고 자식도 없으면, 데이터가 하나뿐인 것
  • 자식이 1개인 경우 예외처리
    -> 삭제하려는 노드가 루트 노드일 경우 그냥 그 자식이 루트 노드가 되면 된다.

정의

#include <iostream>
#include <map>
#include <set>
#include <string>
#include "CBST.h"

using std::wcout;
using std::endl;
using std::map;
using std::make_pair;
using std::set;
using std::wstring;

// 열거형
enum MY_TYPE
{
	TYPE_1, // 0
	TYPE_2, // 1
	TYPE_3, // 2
};

//#define MAN		1
//#define WOMAN	2

struct tStdInfo
{
	wchar_t szName[20];
	unsigned char age;
	unsigned char gender;

	tStdInfo()
		: szName{}
		, age(0)
		, gender(0)
	{
	}

	tStdInfo(const wchar_t* _pName, unsigned char _age, unsigned char _gender)
		: szName{}
		, age(_age)
		, gender(_gender)
	{
		wcscpy_s(szName, _pName);
	}
};

class MyClass
{
private:
	int a;
public:
	bool operator < (const MyClass& _other) const
	{
		if (a < _other.a)
			return true;
		else
			return false;
	}
};

int main()
{
	// 이진탐색트리
	// 1. 이진탐색을 사용할 수 있게 고안된 이진트리
	// 2. 데이터 입력 시 log(N) 효율
	// 3. 탐색 효율은 log(N)
	// 4. 트리의 모양이 밸런스가 유지되지 않으면 제대로 된 탐색
	// 효율이 나오지 않는다.
	// -> 자가균형 기능 필요
	// (이 기능 잇는건AVL, Red/Black 알고리즘 등이 있음)

	//set<int> setInt;
	//setInt.insert(100);

	////학생정보로 map 설명 예시..
	//map<const wchar_t*, tStdInfo> mapData;

	//tStdInfo info(L"홍길동", 18, MAN);
	//tStdInfo info2(L"이지혜", 25, WOMAN);

	//mapData.insert(make_pair(L"홍길동", info));
	//mapData.insert(make_pair(L"이지혜", info2));

	//wchar_t szFind[20] = L"이지혜";

	//map<const wchar_t*, tStdInfo>::iterator mapiter;
	//mapiter = mapData.find(szFind);

	//// 또 이거 안쓰니까 출력이안댐 . .
	//_wsetlocale(LC_ALL, L"korean");

	//// 데이터 찾지 못함
	//if (mapiter == mapData.end())
	//{
	//	wcout << L"데이터를 찾을 수 없다." << endl;
	//}
	//else
	//{
	//	wcout << L"이름 : " << mapiter->second.szName << endl;
	//	wcout << L"나이 : " << mapiter->second.age << endl;
	//	wcout << L"성별 : ";
	//	if (MAN == mapiter->second.gender)
	//	{
	//		wcout << L"남자" << endl;
	//	}
	//	else if (WOMAN == mapiter->second.gender)
	//	{
	//		wcout << L"여자" << endl;
	//	}
	//	else
	//	{
	//		wcout << L"성별을 알 수 없음" << endl;
	//	}
	//}

	//map<MyClass, tStdInfo> mapStdInfo;
	//MyClass a;
	//mapStdInfo.insert(make_pair(a, info));


	//wstring str;

	CBST<int, int> bstint;

	bstint.insert(make_bstpair(100, 0)); //			100
	bstint.insert(make_bstpair(150, 0)); //		50		150
	bstint.insert(make_bstpair(50, 0));  //	 25	  75  125	175
	bstint.insert(make_bstpair(25, 0));
	bstint.insert(make_bstpair(75, 0));
	bstint.insert(make_bstpair(125, 0));
	bstint.insert(make_bstpair(175, 0));

	CBST<int, int>::iterator Iter = bstint.begin();
	Iter = bstint.find(150);
	Iter = bstint.erase(Iter);

	Iter = bstint.find(100);
	Iter = bstint.erase(Iter);

 	return 0;
}

---

[참고]
https://youtu.be/nI7OvpF0y4Q tree(7)
https://youtu.be/HtI_0WXjCGY tree(8)
https://youtu.be/nFFtB9r7TAI tree(9)
https://youtu.be/PaoNFmlcYwU tree(10)
https://assortrock.com/m/48 이진탐색트리