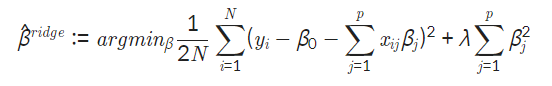0. 들어가기전

Regularization과 Normalization 무슨 차이가 있을까?

Regularization은 정칙화로 불리며 오버피팅을 해결하는 방법 중 하나이다.
L1 Regularization, L2 Regularization, Dropout, Batch normalization 등이 있다.
Regularization 기법들은 모델의 train set의 정답을 맞히지 못하도록 (train set에 과적합되지않도록) 방해하는 역할을 한다. 그래서 train loss는 약간 증가하지만 결과적으로, validation loss나 최종적인 test loss를 감소시킬 수 있다.

Normalization은 정규화라고 불리며 데이터의 형태를 의미있게 전처리하는 과정이다.
데이터를 z-score로 바꾸거나, minmaxscaler를 사용하여 0과 1사이의 값으로 분포를 조정하는 것들이 해당된다.

1. L1 regularization (Lasso)

L1 Regularization 정의

$\beta_0는 절편,\beta_1은 기울기$
마지막 항이 없다면 그냥 Linear Regression이다.

절편에 대해서 미분하면 λ가 사라지므로 Regularization의 효과를 볼 수 없다. X가 1차원 값인 선형 회귀분석 같은 경우 L1 Regularization이 의미가 없다는 뜻이다.

그러므로 L1 Regularization을 사용할 때는 X가 2차원 이상인 여러 컬럼 값이 있는 데이터일 때 실제 효과를 볼 수 있다.

LinearRegression vs L1 regularization

LinearRegression

from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, mean_squared_error

wine = load_wine()
wine_df = pd.DataFrame(data=wine.data, columns=wine.feature_names)
target_df = pd.DataFrame(data=wine.target, columns=['Y'])

X_train, X_test, y_train, y_test = train_test_split(wine_df, target_df, test_size=0.3, random_state=101)

model = LinearRegression()
model.fit(X_train, y_train)

model.predict(X_test)
pred = model.predict(X_test)

print("result of linear regression")
print('Mean Absolute Error:', mean_absolute_error(y_test, pred))
print('Mean Squared Error:', mean_squared_error(y_test, pred))
print('Mean Root Squared Error:', np.sqrt(mean_squared_error(y_test, pred)))

print("\n\n coefficient linear regression")
print(model.coef_)

L1 regularization

from sklearn.linear_model import Lasso
from sklearn.metrics import mean_absolute_error, mean_squared_error

L1 = Lasso(alpha=0.05)
L1.fit(X_train, y_train)

pred = L1.predict(X_test)

print("result of Lasso")
print('Mean Absolute Error:', mean_absolute_error(y_test, pred))
print('Mean Squared Error:', mean_squared_error(y_test, pred))
print('Mean Root Squared Error:', np.sqrt(mean_squared_error(y_test, pred)))

print("\n\n coefficient of Lasso")
print(L1.coef_)

라쏘규제를 추가한 것과 안한 것의 coef 차이는 크다.
라쏘규제를 안한 Linear Regression에서는 모든 칼럼의 가중치를 탐색하여 구하는 반면, 라쏘규제를 추가한 L1 Regularization에서는 총 13개 중 7개를 제외한 나머지의 값들이 모두 0임을 확인할 수 있다.

error부분에서는 큰 차이가 없지만 L1 규제를 통해 어떤 칼럼이 결과에 영향을 더 크게 미치는지 확인할 수 있다. 차원 축소와 비슷한 개념으로 변수의 값을 7개만 남겨도 충분히 결과를 예측할 수 있다는 것이다.

2. L2 Regularization(Ridge)

L2 Regularization 정의

L1과 L2의 차이점을 아시겠나요?

L1 규제는 마지막 항에 ∣β∣를 사용하여 마름모 형태의 제약조건이 생기고, L2 규제는 마지막 항에 $β^2$ 을 사용하여 원의 형태로 나타나게 됩니다.

L2 규제는 절편에 대해서 미분을 하여도 일차항들이 남아있어서 완전히 0에 가지 않는다.
또한 제곱이 들어가있어서 크기가 큰 가중치에 대해서는 규제를 강하게, 작은 가중치에 대해서는 규제를 약하게 줘서 모든 가중치들이 모델에게 고르게 반영되도록 하고, L1 규제보다 수렴이 빠르다는 장점이 있다.

L1 regularization vs L2 regularization

1. L1 regularization

iteration 횟수를 5회로 두었다.

from sklearn.linear_model import Lasso

L1 = Lasso(alpha=0.05, max_iter=5)
L1.fit(X_train, y_train)
pred = L1.predict(X_test)

print("result of Lasso")
print('Mean Absolute Error:', mean_absolute_error(y_test, pred))
print('Mean Squared Error:', mean_squared_error(y_test, pred))
print('Mean Root Squared Error:', np.sqrt(mean_squared_error(y_test, pred)))

print("\n\n coefficient of Lasso")
print(L1.coef_)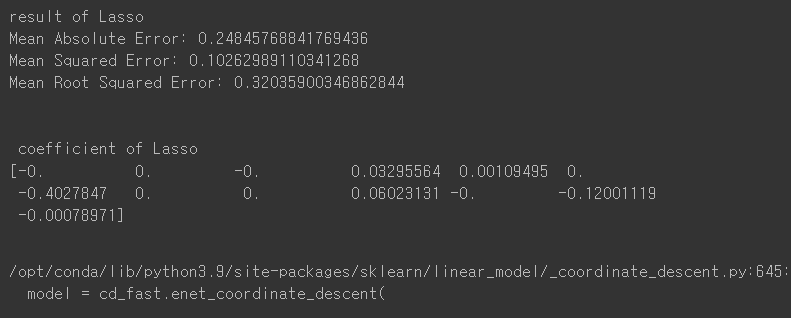

2. L2 regularization

마찬가지로 iteration 횟수를 5회로 두었다.

from sklearn.linear_model import Ridge

L2 = Ridge(alpha=0.05,max_iter=5)
L2.fit(X_train, y_train)
pred = L2.predict(X_test)

print("result of Ridge")
print('Mean Absolute Error:', mean_absolute_error(y_test, pred))
print('Mean Squared Error:', mean_squared_error(y_test, pred))
print('Mean Root Squared Error:', np.sqrt(mean_squared_error(y_test, pred)))

print("\n\n coefficient of Ridge")
print(L2.coef_)

iteration 값을 5로 설정했을 때,
L2 규제 문제는 Linear Regression과 같은 값이 나오지만 L1 Regularization에서는 아직 수렴하지않아서 앞 step과 같은 값을 확인할 수가 없다.

정리하자면, L1 규제는 가중치가 작은 벡터를 0으로 보내면서 차원 축소와 비슷한 역할을 하고
L2 규제는 가중치가 작은 벡터를 0에 가깝게 보내지만 0에 완전히 보내진 않는다. 그러고 제곱항이라서 수렴 속도가 빠르다. 데이터에 따라 적절한 Regularization 방법을 활용하는 것이 좋다!!

3. Dropout

Fully connected layer에서 오버피팅이 생기는 경우에 주로 Dropout layer를 추가한다.

확률적으로 랜덤하게 몇 가지의 뉴런만 선택하여 정보를 전달함으로써 오버피팅을 막는다.
드롭아웃 비율을 너무 늘리면 제대로 전달되지 않아 학습이 잘 안되고, 드롭아웃 비율을 너무 작게하면 fully connected layer나 다름이 없다.

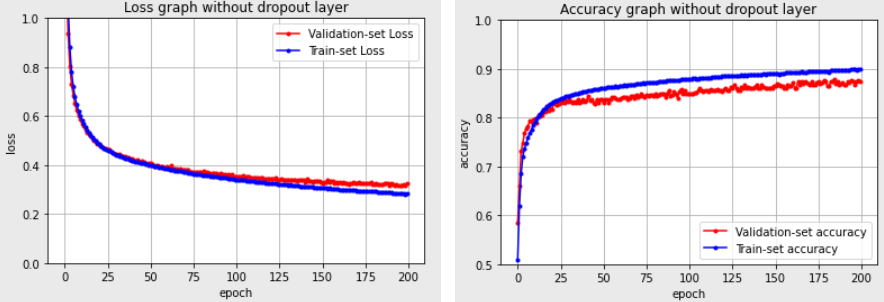
오버피팅 된 fully connected layer

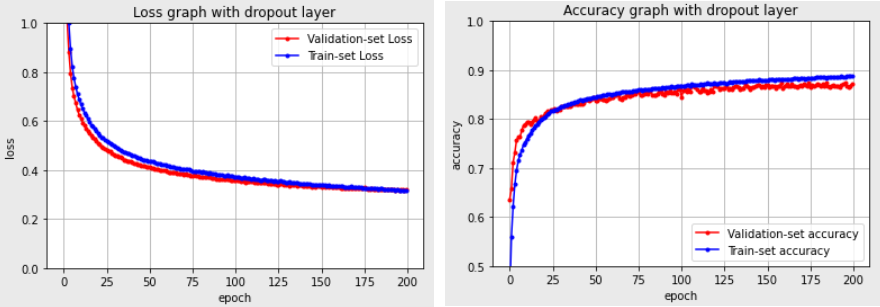
dropout layer를 추가해서 오버피팅을 막음

4. Batch Normalization

Batch Normalization은 기울기 소실,폭발을 해결하는 방법이다.

Batch Normalization layer 추가

Batch Normalization layer 추가하였더니 좀 더 빠르게 정확도가 상승하고 손실 함수의 감소도 더 빨라짐을 확인할 수 있다. Batch Normalization으로 인해 이미지가 정규화되면서 좀 더 고른 분포를 가지며 안정적인 학습이 가능해진다.