[ALGORITHMS] Divide and Conquer

1. Divide and Conquer란?

Divide and Conquer (분할 정복)는 문제 해결 전략 중 하나로, 다음의 세 가지 단계로 구성됩니다:

• Divide (분할) : 문제를 동일한 유형의 더 작은 하위 문제들로 나눈다.
• Conquer (정복) : 하위 문제들을 재귀적으로 해결한다.
• Combine (결합) : 하위 문제들의 해를 적절하게 결합하여 원래 문제의 해를 구한다.

2. 재귀(Recursive) 방식

• 재귀적인 방법은 Divide and Conquer와 밀접한 관련이 있음.
• 큰 문제를 더 작은 문제로 나눠서 해결하고, 그 해답을 이용해 큰 문제를 푸는 방식.
• 비재귀적(non-recursive) 방법이 더 빠를 수도 있음. 예: 동적 계획법(Dynamic Programming)

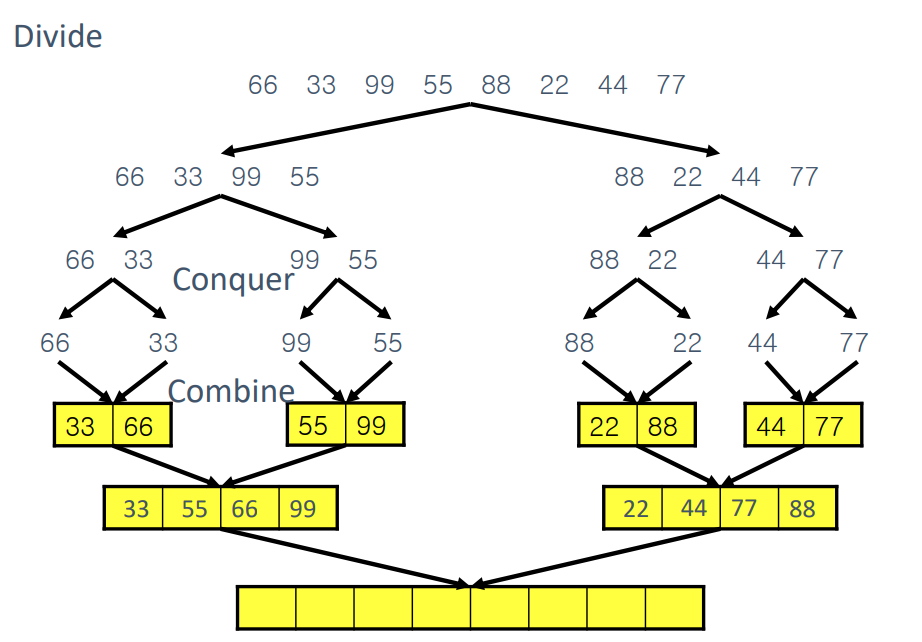
3. 예제: Merge Sort

• Merge Sort는 Divide and Conquer를 대표하는 알고리즘입니다.
• 단계별 정리:
  1) 숫자 리스트를 계속 절반씩 분할 (Divide)
  2) 각 부분을 정렬하며 병합 (Conquer + Combine)
  

---

예시 문제 1) Merge Sort

public class MergeSort {
    // 메인 정렬 함수
    public static void mergeSort(int[] arr, int left, int right) {
        if (left < right) {
            // 배열을 둘로 나누기
            int mid = (left + right) / 2;

            // 왼쪽 절반 정렬
            mergeSort(arr, left, mid);

            // 오른쪽 절반 정렬
            mergeSort(arr, mid + 1, right);

            // 병합
            merge(arr, left, mid, right);
        }
    }

    // 병합 함수: 정렬된 두 배열을 하나로 병합
    public static void merge(int[] arr, int left, int mid, int right) {
        // 크기 계산
        int n1 = mid - left + 1;
        int n2 = right - mid;

        // 임시 배열 생성
        int[] L = new int[n1];
        int[] R = new int[n2];

        // 데이터 복사
        for (int i = 0; i < n1; i++)
            L[i] = arr[left + i];
        for (int j = 0; j < n2; j++)
            R[j] = arr[mid + 1 + j];

        // 병합 과정
        int i = 0, j = 0, k = left;
        while (i < n1 && j < n2) {
            if (L[i] <= R[j]) {
                arr[k] = L[i];
                i++;
            } else {
                arr[k] = R[j];
                j++;
            }
            k++;
        }

        // 남은 요소 복사
        while (i < n1) {
            arr[k] = L[i];
            i++;
            k++;
        }
        while (j < n2) {
            arr[k] = R[j];
            j++;
            k++;
        }
    }

    // 테스트
    public static void main(String[] args) {
        int[] arr = { 38, 27, 43, 3, 9, 82, 10 };
        mergeSort(arr, 0, arr.length - 1);

        // 출력
        for (int num : arr) {
            System.out.print(num + " ");
        }
    }
}

예시 문제 2)

Problem Description

Given an integer, implement an algorithm using the divide and conquer approach with the following rules:

1. If the number of digits is 1, return the digit.

2. If the number of digits is 2, return the product of the two digits.

3. If the number of digits is even (2n), split into two halves, solve each recursively, and multiply the results.

4. If the number of digits is odd (2n+1), split into two halves around the middle digit, solve each recursively, multiply the results, and add the middle digit.

API

public int processDigits(String num)

input: A single integer with up to 100,000 digits.

output: A single integer results computed using the described process.

constraints:

• Input integer contains only digits (0-9).

• No leading zeros except when the number is 0.

Main method for Test

public class Main {

public static void main(String[] args) {

        Itm  itm = new Itm();

         System.out.println("24: "+(itm.processDigits("1234")==24?24:-1));   // Output: 24

          System.out.println("43: "+(itm.processDigits("12345")==43?43:-1));  // Output: 43

}

}

Solution

public class Itm {
  public int processDigits(String s) {
    int num = Integer.parseInt(s);
    int len = s.length();

    if (len == 1) {
      return num;
    } else if (len == 2) {
      return (num%10) * (num/10);
    }

    if (num % 2 == 0) {
      String left = s.substring(0, len/2);
      String right = s.substring(len/2);
      return processDigits(left) * processDigits(right);
    } else {
      String left = s.substring(0, len/2);
      int mid = Integer.parseInt(s.substring(len/2, len/2 + 1));
      String right = s.substring(len/2 + 1);
      return processDigits(left) * processDigits(right) + mid;
    }
  }
}