문제

많은 공장에서 로봇이 이용되고 있다. 우리 월드 공장의 로봇은 바라보는 방향으로 궤도를 따라 움직이며, 움직이는 방향은 동, 서, 남, 북 가운데 하나이다. 로봇의 이동을 제어하는 명령어는 다음과 같이 두 가지이다.

• 명령 1. Go k: k는 1, 2 또는 3일 수 있다. 현재 향하고 있는 방향으로 k칸 만큼 움직인다.
• 명령 2. Turn dir: dir은 left 또는 right 이며, 각각 왼쪽 또는 오른쪽으로 90° 회전한다.

공장 내 궤도가 설치되어 있는 상태가 아래와 같이 0과 1로 이루어진 직사각형 모양으로 로봇에게 입력된다. 0은 궤도가 깔려 있어 로봇이 갈 수 있는 지점이고, 1은 궤도가 없어 로봇이 갈 수 없는 지점이다. 로봇이 (4, 2) 지점에서 남쪽을 향하고 있을 때, 이 로봇을 (2, 4) 지점에서 동쪽으로 향하도록 이동시키는 것은 아래와 같이 9번의 명령으로 가능하다.

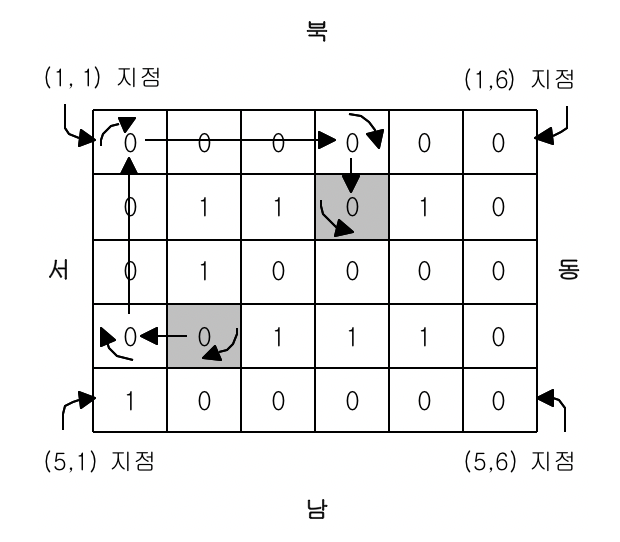
로봇의 현재 위치와 바라보는 방향이 주어졌을 때, 로봇을 원하는 위치로 이동시키고, 원하는 방향으로 바라보도록 하는데 최소 몇 번의 명령이 필요한지 구하는 프로그램을 작성하시오.

입력

첫째 줄에 공장 내 궤도 설치 상태를 나타내는 직사각형의 세로 길이 M과 가로 길이 N이 빈칸을 사이에 두고 주어진다. 이때 M과 N은 둘 다 100이하의 자연수이다. 이어 M줄에 걸쳐 한 줄에 N개씩 각 지점의 궤도 설치 상태를 나타내는 숫자 0 또는 1이 빈칸을 사이에 두고 주어진다. 다음 줄에는 로봇의 출발 지점의 위치 (행과 열의 번호)와 바라보는 방향이 빈칸을 사이에 두고 주어진다. 마지막 줄에는 로봇의 도착 지점의 위치 (행과 열의 번호)와 바라보는 방향이 빈칸을 사이에 두고 주어진다. 방향은 동쪽이 1, 서쪽이 2, 남쪽이 3, 북쪽이 4로 주어진다. 출발지점에서 도착지점까지는 항상 이동이 가능하다.

출력

첫째 줄에 로봇을 도착 지점에 원하는 방향으로 이동시키는데 필요한 최소 명령 횟수를 출력한다.

import java.io.*;
import java.util.*;

public class Main {
    static int N, M, result;
    static int[][] arr;
    static boolean[][][] V;
    static int[] dx = { -1, 0, 1, 0 };
    static int[] dy = { 0, 1, 0, -1 };
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;
        st = new StringTokenizer(br.readLine());
        N = Integer.parseInt(st.nextToken());
        M = Integer.parseInt(st.nextToken());
        arr = new int[N][M];
        for (int i = 0; i < N; i++) {
            st = new StringTokenizer(br.readLine());
            for (int j = 0; j < M; j++) {
                arr[i][j] = Integer.parseInt(st.nextToken());
            }
        }
        Node[] node = new Node[2];
        for (int i = 0; i < 2; i++) {
            st = new StringTokenizer(br.readLine());
            int x = Integer.parseInt(st.nextToken())-1;
            int y = Integer.parseInt(st.nextToken())-1;
            int dir = Integer.parseInt(st.nextToken());
            if (dir == 1) // 동
                dir = 1;
            else if(dir == 2) // 서
                dir = 3;
            else if (dir == 3) // 남
                dir = 2;
            else if (dir == 4) // 북
                dir = 0;
            node[i] = new Node(x, y, dir, 0);
        }
        BFS(node[0], node[1]);
        System.out.println(result);

    }
    public static void BFS(Node start, Node end) {
        Queue<Node> q = new LinkedList<>();
        V = new boolean[4][N][M];
        q.add(start);
        V[start.dir][start.x][start.y] = true;

        while(!q.isEmpty()) {
            Node n = q.poll();
            if (n.x == end.x && n.y == end.y && n.dir == end.dir) {
                result = n.cnt;
                return;
            }
            // 해당 방향으로 최대 3칸 이동.
            for (int i = 1; i <= 3; i++) {
                int nx = n.x + dx[n.dir] * i;
                int ny = n.y + dy[n.dir] * i;
                if (nx < 0 || ny < 0 || nx >= N || ny >= M || arr[nx][ny] == 1)
                    break; // 범위를 벗어나면 더 이상 진행의 의미가 없다.
                if (V[n.dir][nx][ny])
                    continue;
                V[n.dir][nx][ny] = true;
                q.add(new Node(nx, ny, n.dir, n.cnt+1));
            }
            // 방향 전환.
            for (int i = 1; i < 4; i++) {
                int cnt = i != 3 ? i : 1; // 방향 전환 횟수. 3번 회전은 1번 회전과 같음.
                int ndir = (n.dir + i) % 4; // 갈 수 있는 방향.
                if (V[ndir][n.x][n.y])
                    continue;
                V[ndir][n.x][n.y] = true;
                q.add(new Node(n.x, n.y, ndir, n.cnt+cnt));
            }
        }
    }
}
class Node {
    int x, y, dir, cnt;
    Node (int x, int y, int dir, int cnt) {
        this.x = x;
        this.y = y;
        this.dir = dir;
        this.cnt = cnt;
    }
}

• 크게 전진, 회전. 두가지 로직이 필요.
• static int[] dx, dy를 북동남서 순으로 정렬.
• 출발지점과, 끝지점 입력값을 받을 때 dx, dy와 정렬되게 값 초기화. -> 1234가 아닌 0123으로 정렬.
• 추상적으로 어떻게 해결할지는 생각났지만 로직구성에서 애먹은 문제.
• 내가 알던 상하좌우의 개념을 다시 정립할 수 있던 기회.