정렬 - 힙 정렬

오늘은 힙 정렬에 대해 알아보자.
힙 정렬(heap sort)은 힙(heap)을 이용하여 정렬하는 알고리즘이다.

📘 힙이란?

힙은 '부모의 값이 자식의 값보다 항상 크다' 라는 조건을 만족하는 완전이진트리이다. 이때 부모의 값이 자식보다 항상 작아도 힙이라고 한다.(부모와 자식 요소의 관계만 일정하면 된다.)

힙 정렬은 힙을 기반으로 사용되는 알고리즘이므로 힙에 대해 먼저 알아보자.

✏ 트리

트리(tree)가 무엇인지 알아보자.

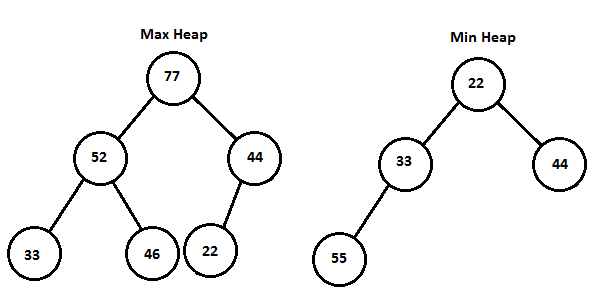
위와같은 구조를 Tree 구조라고 한다. 위 그림을 거꾸로 보면 나무같이 생겨서 tree구조라고 한다. 여기서 몇 가지 알아야 할 것이 있다. 이 부분만 짚자면 아래와 같다.

📜 부모 노드(parent node) : 자기 자신(노드)과 연결 된 노드 중 자신보다 높은 노드를 의미
(ex. 52의 부모노드 : 77)
📜 자식 노드(child node) : 자기 자신(노드)과 연결 된 노드 중 자신보다 낮은 노드를 의미
(ex. 77의 자식노드 : 52, 44)
📜 루트 노드 (root node) : 일명 뿌리 노드라고 하며 루트 노드는 하나의 트리에선 하나밖에 존재하지 않고, 부모노드가 없다.
(ex. 왼쪽 트리에선 77, 오른쪽 트리에선 22)
📜 단말 노드(leaf node) : 리프 노드라고도 불리며 자식 노드가 없는 노드를 의미한다.
(ex. 왼쪽 트리에선 33, 46, 22)
📜 내부 노드(internal node) : 단말 노드가 아닌 노드
📜 형제 노드(sibling node) : 부모가 같은 노드를 말한다.
(ex. 왼쪽 트리에서 33, 46은 모두 부모노드가 52이므로 33, 46은 형제노드다.)
📜 깊이(depth) : 특정 노드에 도달하기 위해 거쳐가야 하는 '간선의 개수'를 의미
(ex. 46의 깊이 : 77->52->46 이므로 깊이는 2가 됨)
📜 레벨(level) : 특정 깊이에 있는 노드들의 집합을 말하며, 구현하는 사람에 따라 0 또는 1부터 시작한다.
📜 차수(degree) : 특정 노드가 하위(자식) 노드와 연결 된 개수
(ex. 52의 차수 = 2 {33, 46})

✏ 완전이진트리

힙은 완전이진트리이므로 완전이진트리를 알아보자.

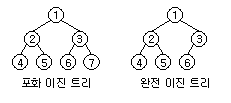
'완전 이진 트리'란 먼저 정의하자면 '마지막 레벨'을 제외한 모든 노드가 채워져있으면서 모든 노드(=사실상 마지막 레벨의 노드들)가 왼쪽부터 채워져있어야 한다.

즉, 완전 이진 트리는 이진 트리에서 두 가지 조건을 더 만족해야 하는 것이다.

1. 마지막 레벨을 제외한 모든 노드가 채워져 있다.
2. 모든 노드들은 왼쪽부터 채워져 있다.

그리고 완전 이진 트리에서 한 가지 조건만 더 추가하면 '포화 이진 트리(perfect binary tree)'가 된다. 바로 '마지막 레벨을 제외한 모든 노드는 두 개의 자식노드를 갖는다'라는 조건이다.

✏ 힙(Heap)

힙은 이진트리의 일종이다.

반정렬 상태(정렬된 상태가 아니다)이며, 완전이진트리와는 다르게 중복값이 허용된다.
삽입/삭제는 트리 구조이기 때문에 O(logN)이므로 매우 빠르다.

보통 우선순위 큐가 힙으로 많이 구현되는데, 배열과 리스트보다 효율적이다.

힙은 최대힙, 최소힙으로 나뉘어진다. 최대힙은 부모노드가 자식노드보다 큼 이라는 특징을 가지고 최소힙은 부모노드가 자식노드보다 작음 이라는 특징을 가지고 있다. 이러한 특징으로 힙에 값을 넣게 되면 최소힙에서는 최소값 순으로, 최대힙에서는 최대값 순으로 값을 얻을수 있다.

힙 자료구조는 보통 배열을 사용하며, 0번째 인덱스는 계산을 편하게 하기위해 사용하지 않는다. 부모노드의 인덱스가 1이 되어진다

1번째 인덱스부터 시작하며, 해당 인덱스의 자식 노드는 각각 1x2, 1x2 +1로 나타낼수 있다. 결국 모든 부모와 자식 간의 인덱스 관계는 부모:N, 왼쪽자식:2N, 오른쪽자식: 2N+1 를 가진다.

📘 힙 정렬

힙 정렬은 '가장 큰 값이 루트에 위치'하는 특징을 이용하는 정렬 알고리즘이다.
힙에서 가장 큰 값인 루트를 꺼내는 작업을 반복하고 그 값을 늘어놓으면 배열은 정렬을 마치게 된다.
즉, 힙 정렬은 선택 정렬을 응용한 알고리즘이며 힙에서 가장 큰 값인 루트를 꺼내고 남은 요소에서 다시 가장 큰 값을 구해야 한다.

위를 정리하면

1. 루트를 꺼낸다.
2. 마지막 요소를 루트로 이동한다.
3. 자기보다 큰 값을 가지는 자식 요소와 자리를 바꾸며 아래쪽으로 내려가는 작업을 반복한다.
   이때 자식의 값이 작거나 앞에 다다르면 작업이 종료된다.

✏ 힙 정렬 알고리즘

이제 이 힙을 이용해 힙 정렬 알고리즘으로 확장하면 된다.

알고리즘을 설명하면

1. 힙의 루트(a[0])에 있는 가장 큰 값(10)을 꺼내 배열 마지막 요소(a[9])와 바꾼다.
2. 가장 큰 값을 a[9]로 옮기면 a[9]는 정렬을 마치게 된다.
   그 다음 두 번째로 큰 요소인 9가 루트에 위치하게 된다. 
   힙의 루트 a[0]에 있는 가장 큰 값인 9를 꺼내 아직 정렬하지 않은 부분의 마지막 요소인 a[8]과 바뀌게 된다.
3. 두 번째로 큰 값을 a[8]로 옮기면 a[8] ~ a[9]는 정렬을 마치게 된다.
   그런 다음 a[0] ~ a[7] 요소를 힙으로 만들어 위의 과정을 반복하면 된다.

이를 반복하면 배열의 마지막부터 큰 값이 차례대로 대입된다. 위의 과정을 간단히 하면 다음과 같다.

1. 변수 i의 값을 n - 1로 초기화한다.
2. a[0]과 a[i]을 바꾼다.
3. a[0], a[1], ..., a[i - 1]을 힙으로 만든다.
4. i의 값을 1씩 줄여 0이 되면 끝이 난다. 그렇지 않으면 '2'로 돌아간다.

이 순서대로 힙 정렬을 수행하면 된다. 그런데 초기 상태의 배열이 힙 상태가 아닐수도 있을 수 있기 때문에 이 과정을 적용하기 전에 배열을 힙 상태로 만들어야 한다.

✏ 힙 정렬 코드

코드로 한번 알아보자.

    // 배열 요소 a[idx1]과 a[idx2]의 값을 바꾸는 메서드
    static void swap(int[] a, int idx1, int idx2) {
        int t = a[idx1];
        a[idx1] = a[idx2];
        a[idx2] = t;
    }

    // a[left] ~ a[right]를 힙으로 만드는 메서드
    static void downHeap(int[] a, int left, int right) {
        int temp = a[left];     // 루트
        int child;              // 큰 값을 가진 노드
        int parent;             // 부모

        for (parent = left; parent < (right + 1) / 2; parent = child) {
            int cl = parent * 2 + 1;        // 루트
            int cr = cl + 1;                // 오른쪽 자식
            child = (cr <= right && a[cr] > a[cl]) ? cr : cl; // 큰 값을 가진 노드를 자식에 대입
            if (temp >= a[child]) break;
            a[parent] = a[child];
        }
        a[parent] = temp;
    }

    // 힙 정렬
    static void heapSort(int[] a, int n) {
    
    	// a[i] ~ a[n - 1]를 힙으로 만들기
        for (int i = (n - 1) / 2; i >= 0; i--) downHeap(a, i, n - 1); 
        
        for (int i = n - 1; i > 0; i--) {
            swap(a, 0, i); // 가장 큰 요소와 아직 정렬되지 않은 부분의 마지막 요소를 교환
            downHeap(a, 0, i - 1); // a[0] ~ a[i - 1]을 힙으로 만들기
        }
    }

downHeap 메서드

배열 a 가운데 a[left] ~ a[right]의 요소를 힙으로 만드는 메서드이다. a[left] 이외에는 모두 힙 상태라고 가정하고 a[left]를 아랫부분의 알맞은 위치로 옮겨 힙 상태를 만든다.

heapSort 메서드

요소의 개수가 n개인 배열 a를 힙 정렬하는 메서드이다. 아래의 2단계로 구성된다.

1. downHeap 메서드를 사용하여 배열 a를 힙으로 만든다.
2. 루트(a[0])에 있는 가장 큰 값을 빼내어 배열 마지막 요소와 바꾸고 배열의 나머지 부분을 다시 힙으로 만드는 과정을
   반복하여 정렬을 수행한다.

✏ 힙 정렬의 시간 복잡도

힙 정렬을 선택 정렬을 응용한 알고리즘이다. 단순 선택 정렬은 정렬되지 않은 영역의 모든 요소를 대상으로 가장 큰 값을 선택한다. 힙 정렬에서는 첫 요소를 꺼내는 것만으로 가장 큰 값이 구해지므로 첫 요소를 꺼낸 다음 나머지 요소를 다시 힙으로 만들어야 그 다음에 꺼낼 첫 요소도 가장 큰 값이 유지가 된다.
따라서 단순 선택 정렬에서 가장 큰 요소를 선택할 때의 시간 복잡도 O(n)의 값을 한 번에 선택할 수 있어 O(1)로 줄일 수 있다. 그 대신 힙 정렬에서 다시 힙으로 만드는 작업의 시간 복잡도는 O(log n)이다.

따라서 단순 선택 정렬은 전체 정렬에 걸리는 시간 복잡도의 값이 O(n^2)이지만 힙 정렬은 힙으로 만드는 작업을 요소의 개수만큼 반복하므로 시간 복잡도의 값이 O(n log n)으로 크게 줄어든다.