[Java] 백준 1865번. 웜홀 (#벨만-포드 알고리즘)

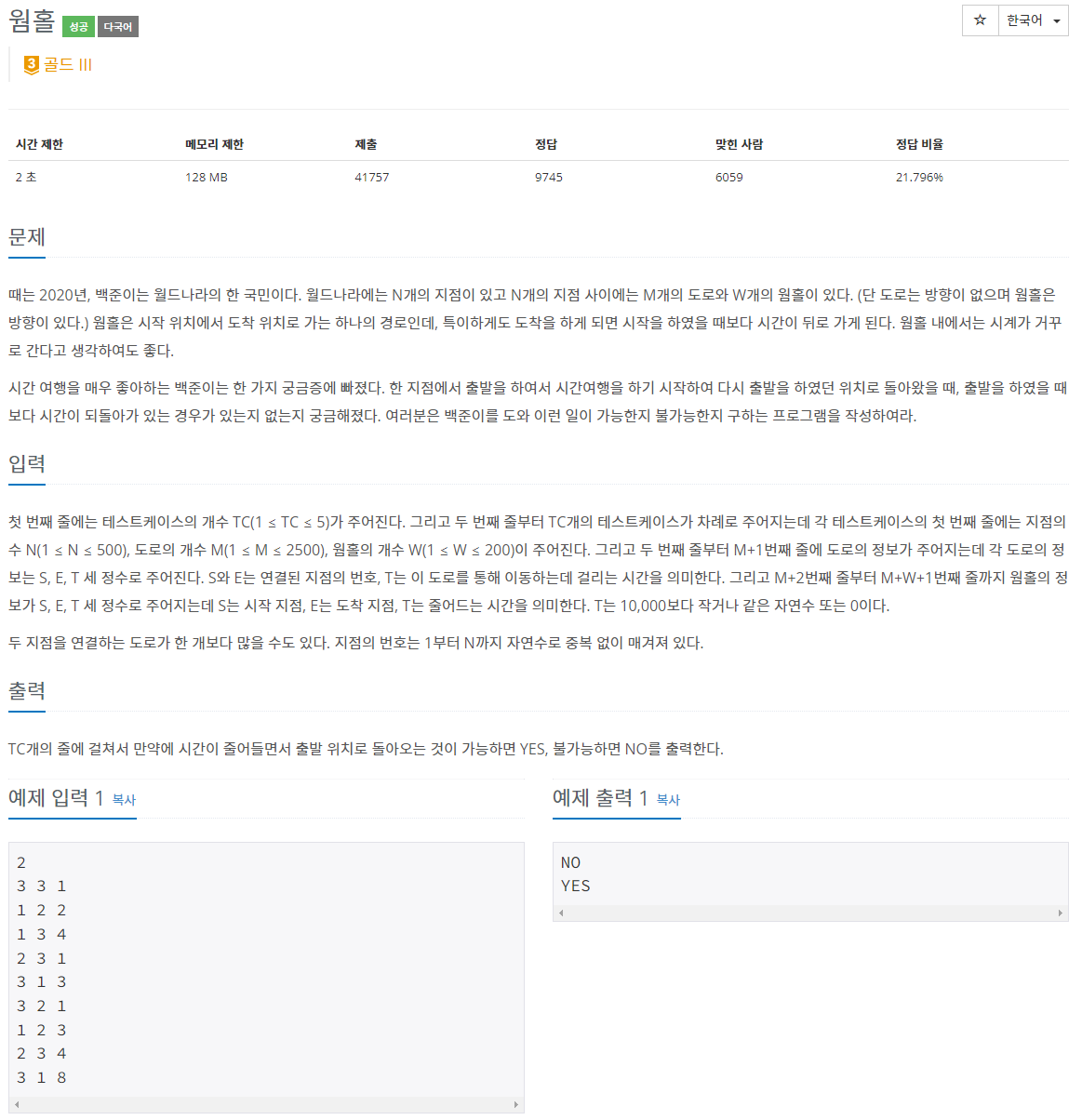
문항출처 : https://www.acmicpc.net/problem/1865

#벨만-포드 알고리즘
노드와 노드 사이의 최소비용 경로를 찾는 알고리즘.
다익스트라 알고리즘과 함께 경로찾기 알고리즘의 양대산맥을 이룬다.

다익스트라 알고리즘의 경우, 벨만-포드 알고리즘보다 시간복잡도는 N^2으로 더 낮지만
비용이 음수인 경우에는 답을 찾을 수가 없다.
반면, 벨만-포드 알고리즘은 비용이 음수인 경우에도 답을 찾을 수가 있지만 시간복잡도가 N^3으로 더 높다.
(단, 벨만-포드 알고리즘에서도 음의 경로 사이클을 갖는 경우에는 답을 찾을 수 없다)
비용이 음수인 경우에 흔치는 않으므로 일반적으로는 다익스트라 알고리즘이 더 빈번하게 사용된다고 볼 수 있다.

다익스트라 알고리즘은
시작노드를 기준으로 나머지 노드의 비용값을 무한대로 놓고 시작하여,
시작노드를 기준으로 연결된 노드의 비용을 갱신하고,
갱신된 노드를 우선순위 큐에 담아 하나씩 다시 꺼내서 그 노드를 기준으로 다시 비용을 갱신하는 것을 반복한다.
따라서 음의 비용이 발생하는 구간은 항상 비용의 갱신이 일어나기 때문에 항상 다시 큐에 담기게 되면서.. 무한루프를 돌게된다.

벨만-포드 알고리즘은
시작노드를 기준으로 나머지 노드의 비용값을 무한대로 놓고 시작하는 것은 동일하지만
모든 비용(경로)를 탐색하여 갱신한다는 차이점이 있다.
벨만-포드 알고리즘에서는 전체 경로를 탐색하여 갱신하는 행위를 (노드의 수)-1번하면 최소비용을 찾을 수가 있다.
벨만-포드 알고리즘에서 음의 사이클이 존재하는지 알고 싶다면
업데이트(전체 경로를 탐색하여 비용을 갱신하는 행위)를
(노드의 수)-1번한 후에 추가적으로 업데이트를 할 때에도 비용이 갱신된다면
음의 사이클이 존재한다고 보고 벨만-포드 알고리즘으로도 답을 찾을 수 없다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.StringTokenizer;

class Main {

    static class Node {
        int index;
        int price;

        public Node(int index, int price) {
            this.index = index;
            this.price = price;
        }
    }

    static ArrayList<Node>[] paths;
    static int n;
    static final int INF = 1000000000;
    static int[] totalPrices;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder sb = new StringBuilder();
        int T = Integer.parseInt(br.readLine());
        for (int test_case = 1; test_case <= T; test_case++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            n = Integer.parseInt(st.nextToken());
            int m = Integer.parseInt(st.nextToken());
            int w = Integer.parseInt(st.nextToken());
			
            //경로 입력받기
            paths = new ArrayList[n + 1];
            for (int i = 1; i <= n; i++) paths[i] = new ArrayList<>();
			
            //양의 경로 입력받기(양방향)
            while (m-- > 0) {
                st = new StringTokenizer(br.readLine());
                int s = Integer.parseInt(st.nextToken());
                int e = Integer.parseInt(st.nextToken());
                int t = Integer.parseInt(st.nextToken());
                paths[s].add(new Node(e, t));
                paths[e].add(new Node(s, t));
            }
            //음의 경로 입력받기(단방향)
            while (w-- > 0) {
                st = new StringTokenizer(br.readLine());
                int s = Integer.parseInt(st.nextToken());
                int e = Integer.parseInt(st.nextToken());
                int t = Integer.parseInt(st.nextToken());
                paths[s].add(new Node(e, -t));
            }

            sb.append(Bellman_Ford() ? "YES\n" : "NO\n");
        }
        System.out.println(sb);
    }

    static boolean Bellman_Ford() {
    	//비용값을 기록할 배열을 만들고 매우 큰값(무한대)로 선언한 후
        //시작 노드를 아무거나 잡아서 비용을 0으로 초기화함
        totalPrices = new int[n + 1];
        Arrays.fill(totalPrices, INF);
        totalPrices[1] = 0;
        
        //비용갱신이 이루어졌는지 확인: 최대 (정점의 개수)-1번 만큼
        boolean isUpdated = false;
        for (int count = 1; count < n; count++) {
             isUpdated = update();
            if (!isUpdated) break;
        }
        if(isUpdated && update()) return true;
        return false;
    }
	
    //모든 경로를 탐색하여 비용갱신이 이루어졌는지 체크하는 업데이트()
    static boolean update(){
        boolean isUpdated = false;
        for (int start = 1; start <= n; start++) {
            for (Node end : paths[start]) {
                if (totalPrices[end.index] > totalPrices[start] + end.price) {
                    totalPrices[end.index] = totalPrices[start] + end.price;
                    isUpdated = true;
                }
            }
        }
        return isUpdated;
    }
}