[Java] 1991번. 트리 순회 (#전위, 중위, 후위 순회)

문항출처 : https://www.acmicpc.net/problem/1991

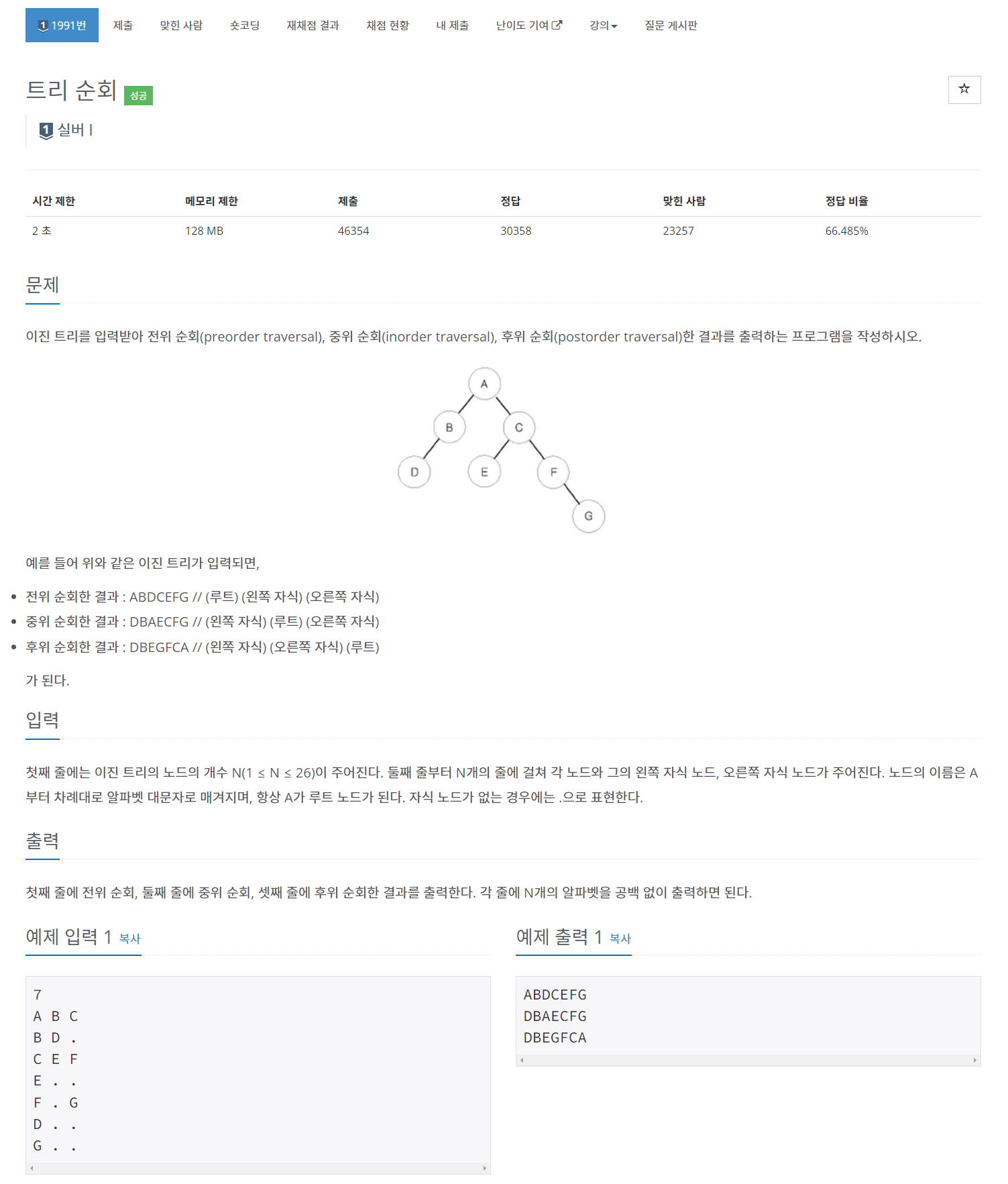
트리 순회에 관한 이론을 알고 있다면 간단한 문제이다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

class Main {
	
     // 그래프의 노드 정보를 담는 클래스
    static class Node{
        char currentChar; // 현재 노드문자
        char leftChild; // 왼쪽자식 노드문자
        char rightChild; // 오른쪽자식 노드문자

        public Node(char currentChar) {
            this.currentChar = currentChar;
            this.leftChild = '0';
            this.rightChild = '0';
        }

        public void setLeftChild(char leftChild) {
            this.leftChild = leftChild;
        }

        public void setRightChild(char rightChild) {
            this.rightChild = rightChild;
        }

    }

    static int n;
    static Node[] graph;
    static StringBuilder sb = new StringBuilder();

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        n = Integer.parseInt(br.readLine()); // 노드의 개수
        graph = new Node[n]; // 노드정보를 담는 노드배열
        while(n-->0){ // 입력받기
            StringTokenizer st = new StringTokenizer(br.readLine());
            char currentChar = st.nextToken().charAt(0); // 부모노드 문자
            int index = currentChar-65; // 배열 graph의 인덱스. ('A'이면 0)
            graph[index] = new Node(currentChar); // 부모노드 문자로 배열에 노드추가
            char leftChild = st.nextToken().charAt(0);
            if(leftChild != '.') graph[index].setLeftChild(leftChild); // 왼쪽자식 노드가 있다면 추가
            char rightChild = st.nextToken().charAt(0);
            if(rightChild != '.') graph[index].setRightChild(rightChild); //오른쪽자식 노드가 있다면 추가
        }
        preorderSearch(graph[0]); // 전위순회(부모,왼쪽,오른쪽 순)
        sb.append("\n");
        inorderSearch(graph[0]); // 중위순회(왼쪽,부모,오른쪽 순)
        sb.append("\n");
        postorderSearch(graph[0]); // 후위순회(왼쪽,오른쪽,부모 순(
        sb.append("\n");
        System.out.println(sb); //출력

    }

    static void preorderSearch(Node node){
    	//현재 노드가 부모노드이므로 출력버퍼에 추가
        sb.append(node.currentChar); 
        //왼쪽노드 탐색
        if(node.leftChild != '0') preorderSearch(graph[node.leftChild-65]); 
        //오른쪽 노드 탐색
        if(node.rightChild != '0') preorderSearch(graph[node.rightChild-65]);
    }
    static void inorderSearch(Node node){
    	//왼쪽노드가 있다면 왼쪽노드부터 탐색하러 들어가야한다.
        if(node.leftChild != '0') inorderSearch(graph[node.leftChild-65]);
        //왼쪽노드가 없다면 현재 노드문자를 출력버퍼에 추가
        sb.append(node.currentChar);
        //오른쪽노드 탐색
        if(node.rightChild != '0') inorderSearch(graph[node.rightChild-65]);
    }
    static void postorderSearch(Node node){
    	//왼쪽노드 탐색
        if(node.leftChild != '0') postorderSearch(graph[node.leftChild-65]);
        //오른쪽노드 탐색
        if(node.rightChild != '0') postorderSearch(graph[node.rightChild-65]);
        //자식노드가 없다면 현재노드를 출력버퍼에 추가
        sb.append(node.currentChar);
    }

}