Cross Entropy Loss
머신러닝에서 모델이 나타내는 확률 분포 Q(x)와 데이터가 따르는 실제 확률 분포 P(x) 사이의 차이를 나타내는 함수를 손실 함수(loss function)라고 한다.
모델의 확률 분포는 파라미터에 따라 달라지기 때문에 손실 함수 역시 파라미터에 따라 바뀐다.
분류(classification) 문제에서는 모델의 출력 결과가 로지스틱 함수(logistic function) 로 표현됨.
분류 클래스가 2개인 로지스틱 함수->시그모이드 함수
클래스가 nn개일 때로 확장한 것이 딥러닝에서도 자주 사용되는 소프트맥스 함수(softmax function).
이 함수와 데이터의 확률 분포의 차이가 분류 문제의 손실 함수.
KL divergence를 최소화하는 것이 cross entropy를 최소화하는 것과 같다
cross entropy 또한 손실 함수의 한 종류
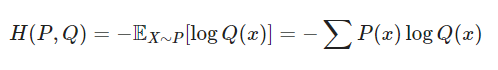
분류 문제에서 데이터의 라벨은 one-hot encoding으로 표현. 클래스의 종류가 NN가지이고 특정 데이터가 nn번째 클래스에 속할 때, nn번째 원소만 1이고 나머지는 0으로 채운 NN차원 벡터로 놓는다.
입력 데이터가 모델을 통과하면 출력 레이어의 소프트맥스 함수에 의해 각각의 클래스에 속할 확률이 계산된다
->이 확률 값들이 모델이 추정한 확률 분포 Q(x)를 구성하는 값들임.
3개의 클래스 c1,c2,c3 가 존재하는 분류 문제에서 어떤 데이터의 출력값이 다음과 같다고 한다면
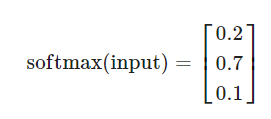
이 결과는 다음 식이 된다.

데이터가 실제로 2번 클래스에 속할 경우, 데이터의 실제 확률 분포는 one-hot encoding과 같은 [0,1,0]이 된다.
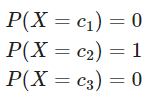
cross entropy를 사용하면 P(x)와 Q(x)의 차이를 다음과 같이 계산할 수 있다.
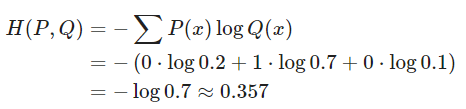
분류 문제에서는 데이터의 확률 분포가 위와 같이 one-hot vector로 표현되기 때문에, P(x)와 Q(x)의 차이를 cross entropy로 계산할 경우 계산이 간단해진다는 장점이 있다.
Cross Entropy와 Likelihood의 관계
모델의 파라미터를 θ로 놓으면
모델이 표현하는 확률 분포: Q(y∣X,θ)
데이터의 실제 분포: P(y∣X)
그런데 Q(y∣X,θ)는 데이터셋과 파라미터가 주어졌을 때 예측값의 분포를 나타내므로 모델의 likelihood와 같다.
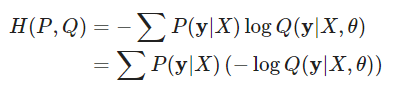
X와 y는 데이터셋에 의해 결정되는 값이기 때문에 모델의 식이 바뀌어도 변하지 않음 -> 관여할 수 없는 값
−logQ(y∣X,θ)만이 바꿀 수 있다.
따라서,
cross entropy를 최소화하는 파라미터 값을 구하는 것은 결국 negative log likelihood를 최소화하는 파라미터를 구하는 것과 같다고 할 수 있다.
