신경망(Neural Network): 뇌에는 1000억 개에 가까운 신경계 뉴런들이 있음. 이 뉴런들은 서로 매우 복잡하게 얽혀 있고, 조금 물러서서 보면 하나의 거대한 그물망과 같은 형태를 이루고 있음. 그것을 신경망이라 함.
머신러닝/딥러닝 과학자들이 자연에서 답을 찾으려 노력했고, 우리 뇌 속의 신경망 구조에 착안해서 퍼셉트론(Perceptron) 이라는 형태를 제안하며 이를 연결한 형태를 인공신경망(Artificial Neural Network)이라고 부름.
다층 퍼셉트론 Overview
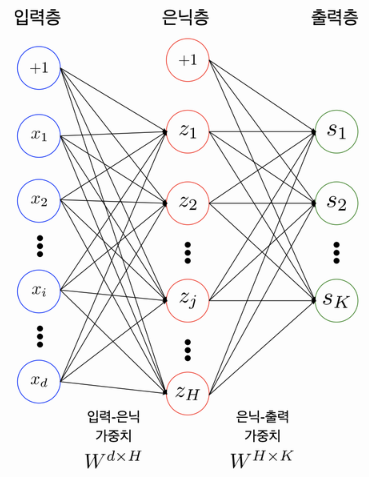
레이어 개수를 셀 때는 노드와 노드 사이의 연결하는 부분이 몇 개 존재하는지 세어야 함. 노드갯수를 세면X.
→ 2개 이상의 레이어를 쌓아서 만든 것을 ’다층 퍼셉트론(Multi-Layer Perceptron; MLP)’
Parameters/Weights
입력층-은닉층, 은닉층-출력층 사이에는 각각 행렬(Matrix)이 존재함.
입력값이 100개, 은닉 노드가 20개라면 입력층-은닉층 사이에는 100x20의 형태를 가진 행렬이 존재.
은닉 노드가 20개, 출력층이 10개의 노드를 가진다면 은닉층-출력층 사이에는 20x10의 형태를 가진 행렬이 존재.
이 행렬들을 Parameter 혹은 Weight라고 부름.
인접한 레이어 사이에는 아래와 같은 관계가 성립.
y=W⋅X+b
활성화 함수와 손실 함수
활성화 함수는 보통 비선형 함수를 사용하는데 이 비선형 함수를 MLP(다층 퍼셉트론) 안에 포함시키면서 ‘모델의 표현력이 좋아지게’ 됨(레이어 사이에 비선형 함수가 포함되지 않은 MLP는 한 개의 레이어로 이루어진 모델과 수학적으로 다른 점 X).
비선형함수
1. Sigmoid
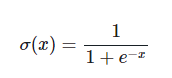
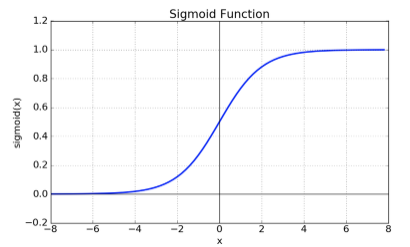
예전부터 많이 써오던 sigmoid 함수, 현재는 ReLU 함수 더 많이 사용.
단점: vanishing gradient 현상이 발생. exp 함수 사용 시 비용이 큼.
2. Tanh
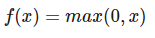
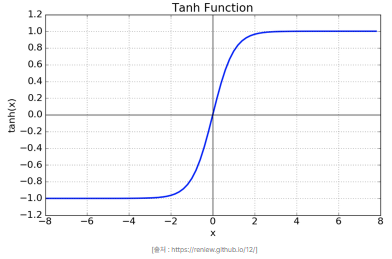
함수의 중심값을 0으로 옮겨 sigmoid의 최적화 과정이 느려지는 문제해결.
vanishing gradient 문제.
3. ReLU
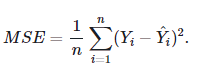
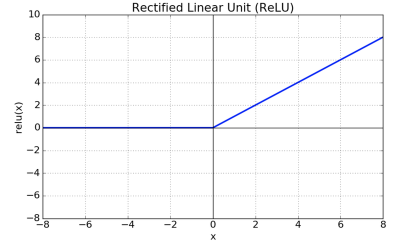
sigmoid, tanh 함수에 비해 학습이 빠름.연산 비용이 크지 않고, 구현이 매우 간단.
손실함수
비선형 활성화 함수를 가진 여러 개의 은닉층을 거친 다음 신호 정보들은 출력층으로 전달됨.
이때 ‘우리가 원하는 정답’과 ‘전달된 신호 정보들’ 사이의 차이를 계산하고, 이 차이를 줄이기 위해 각 파라미터들을 조정하는 것이 딥러닝의 전체적인 학습 흐름
→ 이 차이(오차)를 구하는 데 사용되는 함수가 손실함수(Loss function) 또는 비용함수(Cost function)
대표적으로 두 가지 손실함수
1. 평균제곱오차 (MSE: Mean Square Error)
2. 교차 엔트로피 (Cross Entropy): 두 확률분포 사이의 ‘유사도가 클수록’ ‘작아지는’ 값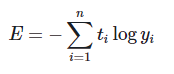
경사하강법(Gradient Descent)
손실함수로 오차를 구했으니 이 오차를 최소화 하는 방법을 찾아야 함 → 경사하강법
1. 우리가 너무 크게 발걸음을 내딛는 거인이라면 산 아래로 효율적으로 내려가지 못하고 또 다른 골짜기에 빠지고 만다. 그래서 우리는 학습률(learning rate) 이라는 개념을 도입해 ‘기울기 값과 이 학습률을 ’곱한 만큼’ 발걸음을 내딛는다.
- 발걸음을 잘 내딛는다 해도 어디서 출발했느냐에 따라 산 아래로 내려가는 시간이 빨라질 수도 느려질 수도 있다. 이는 parameter의 값들을 어떻게 초기화하는지의 문제와 맞닿아 있다.
오차역전파법
손실 함수를 통해 구해진 오차를 가지고 각 파라미터들을 조정하는 경사하강법.
그럼 이 기울기를 어떻게 입력층까지 전달하며 파라미터들을 조정해 나갈 수 있을까?
이 과정에서 쓰이는 개념이 오차역전파(Backpropagation).
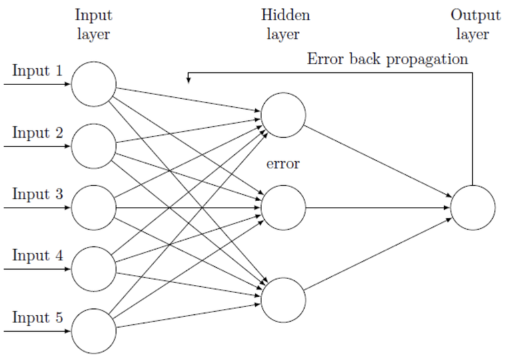
모델 학습 Step-by-Step
Forward Propagation과 Backward Propagation을 통해 학습해야 할 파라미터 W1, b1, W2, b2가 업데이트되면 → 모델이 추론한 확률값 y_hat이 정답의 One-hot 인코딩 t값에 조금씩 근접하는 것과, Loss가 점점 감소하는 것이 확인된다.
학습한 파라미터 W1, b1, W2, b2를 가지고 우리는 숫자를 인식(Predict)해 보고, 그 정확도(Accuracy)를 측정할 수 있다.
