[DeepLearning] 영화 "테넷"이 Diffusion Model 의 핵심이라고?

사실 필자는 테넷을 본 적이 없다...

하지만 필자가 비교하고자 하는 것은 영화 테넷의 핵심 이론중 하나인 열역학 제 2법칙의 엔트로피다. 뭐? 영화 테넷의 핵심 이론이 엔트로피가 아니라고?

열역학 제2법칙 ( Entropy )

갑자기 웬 열역학이라니..참 뜬금없어 보이지 않는가? 하지만 어떻게 보면 이 물리학적 원리가 Diffusion 모델의 핵심 개념이라고도 볼 수 있다. 열역학 제2법칙이 무엇인지 간단하게 알아보자.

열역학 제 2법칙은 엔트로피에 대한 내용이다. 엔트로피를 무질서도 에 빗대어 자주 표현되는데, 이 것은 완전히 정확한 표현은 아니다. 이 것은 우리 인류 관점에서 해석한 표현이다.

열역학 제 2법칙에서 엔트로피는 열의 이동과 관련된 법칙을 일컫는다. 분자 들이 에너지를 골고루 공유하며 가장 높은 확률로 나아가려는 경향성을 띤다. 이 것을 엔트로피가 증가한다고 표현한다.

컵안의 물이 있고 그 안에 잉크물을 떨어트리면 시간이 서서히 흘러가면서 컵안의 물의 색이 잉크물의 색으로 번지기 시작한다. 아래 이미지에 제시된 6가지(A~F) 경우의 수 중 당연히 F의 결과를 채택하게 될 것이다. 그 이유를 알아보자.

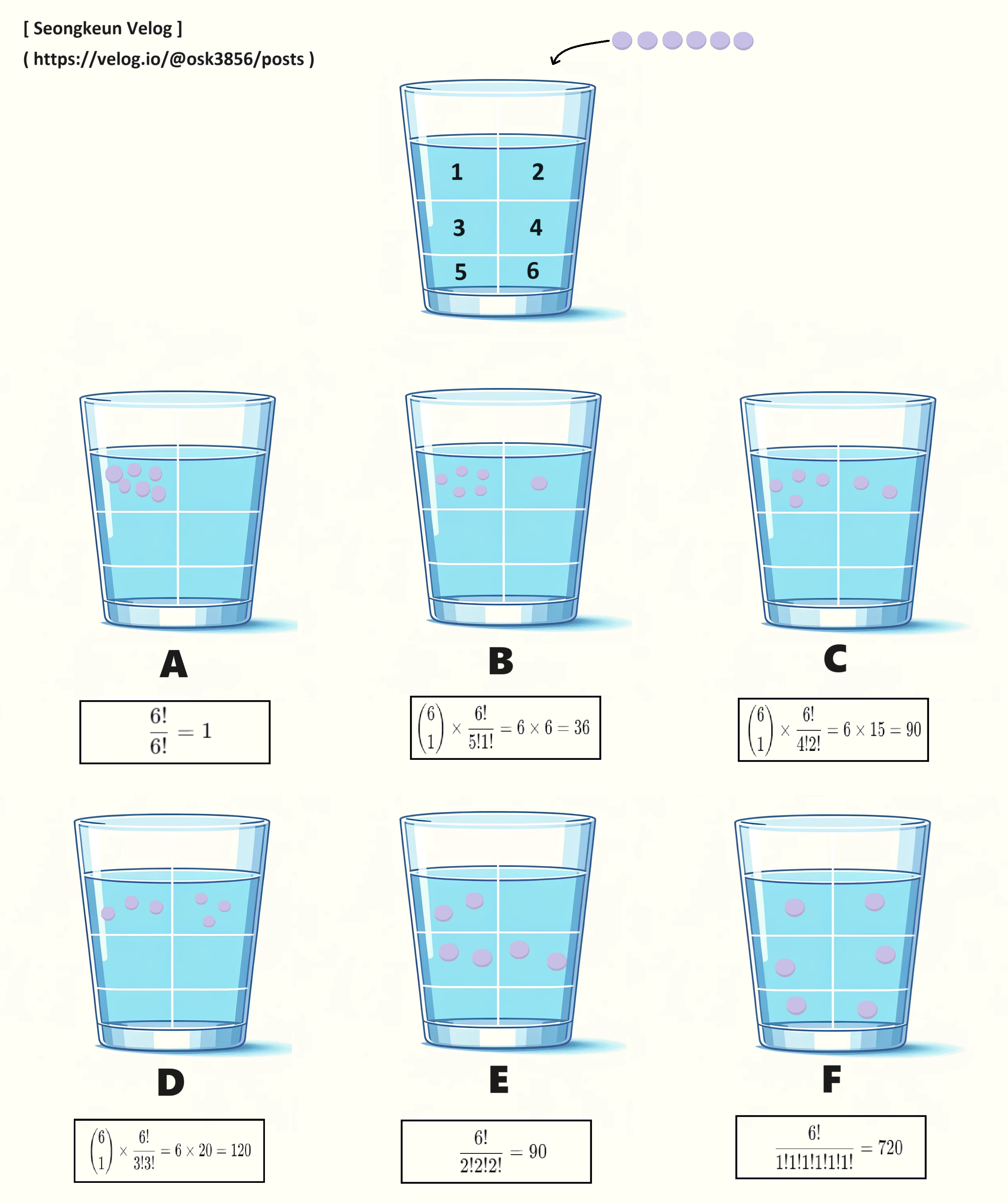
위의 보라색 동그라미는 잉크분자라고 가정한다.

$A$ : 모든 분자가 하나의 구역에 있는 경우

$B$ : 5개의 분자가 하나의 구역에 있고, 나머지 1개가 다른 구역에 있는 경우

$C$ : 4개의 분자가 하나의 구역에 있고, 나머지 2개가 다른 하나의 구역에 있는 경우

$D$ : 3개의 분자가 하나의 구역에 있고, 나머지 3개가 다른 하나의 구역에 있는 경우

$E$ : 각각의 2개 분자가 서로 다른 세 개의 구역에 있는 경우

$F$ : 각 분자가 서로 다른 구역에 있는 경우

"n개 중에서 k개를 선택하는 경우의 수" 는 $_nC_k$ 와 같은 조합식으로 사용할 수 있고 조합계수 $\binom{n}{k}$ 로도 표현한다. 위 B, C, D에서 다수의 잉크 분자를 1번 구역에 고정시켜놓은 형태를 위해 $\binom{6}{1}$ 과 같이 사용하였다. 조합식으로는 $_6C_1$ 과 같이 표현할 수 있다.

물론 위 이미지에 나와있지는 않은 형태의 경우들이 더 많이 존재하겠지만 뭐가 어찌되었든 결론적으로 F 형태로 보라색 잉크 분자가 확산하게 될 것이다. 모든 구역에 균일하게 분포(확산)하는 경우의 수가 가장 높기 때문이다. 엔트로피는 이처럼 경우의 수가 가장 높은 방향으로 흘러간다.

---

엔트로피에서 다른 중요한 키워드는 비가역성이다. 생소한가? 간단한 설명으로 '시간을 거스르지 않는다'는 의미이다. 자연상태로 두었을 때, 얼음이 녹으면 물로 상태변화 하지만 녹은 물은 얼음상태로 되돌아가지 않는다. 이 부분은 열평형에 관한 내용이다. 열역학에 의하면 "열은 높은 곳에서 낮은 곳으로 흐른다." 라는 정도로만 이해하고 넘어가자.

다른 예시를 보자. 아래 이미지는 깨진 도자기 그릇이다. 아래의 그릇이 입자단위로 온전한 그릇으로 존재할 경우의 수는 위상적으로 단 한가지 경우 밖에 없다. 그래서 이미지의 좌측 상태는 엔트로피가 낮은상태 우측 상태는 엔트로피가 높은상태라고 부른다.

본론

자, 이제 Diffusion 모델과 엔트로피가 무슨 연관이 있는지 비교해볼 것이다. 그 전에 Diffusion Model 이 무엇인지 간략하게 알아보자.

Diffusion 모델의 동작 원리

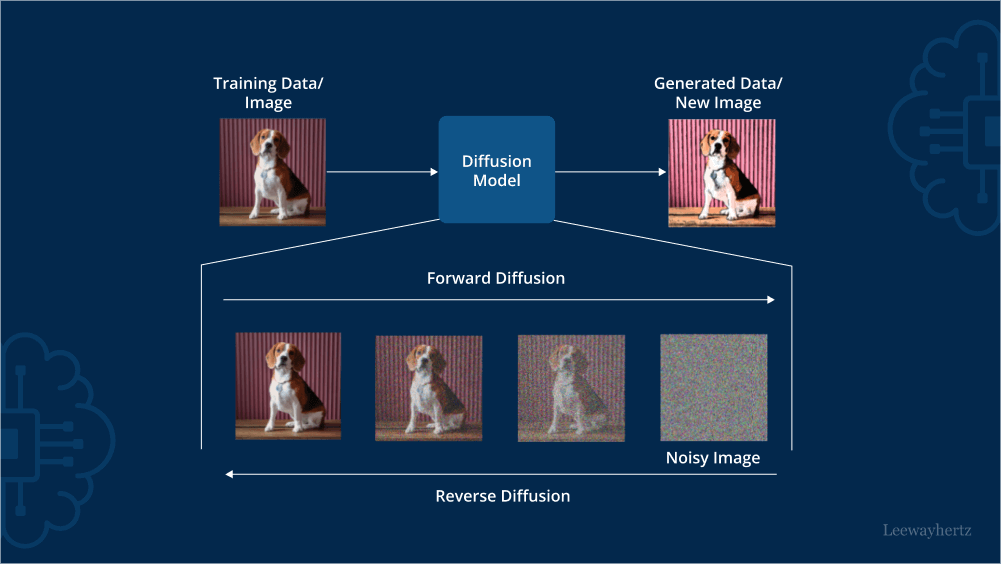
• Forward Diffusion : 노이즈를 추가하는 프로세스
• Reverse Diffusion : 노이즈에서 원본 이미지를 찾아가는 프로세스

Diffusion 모델은 Training 단계에서 입력 데이터에 무작위 노이즈를 추가하는 프로세스(Forward Process)와 노이즈를 제거하며 원본 이미지를 찾아가는 프로세스(Reverse Process)를 갖고있다.

Diffusion Model vs.Entropy

1. 무질서 관점

Forward Process 에서 데이터는 점점 더 무질서 해지며 이 것은 엔트로피의 증가와 유사하다. 노이즈를 제거하면서 데이터의 원래 분포로 되돌리는 Reverse Process 는 엔트로피의 감소와 유사하다고 생각해 볼 수 있다. Reverse Process 를 통해 이미지 데이터를 원래의 분포로 복원하면서 원본 데이터의 feature 를 학습한다.

2. 비가역성

위의 도자기 그릇을 예시로 들어보자. 도자기 그릇은 깨지는 것은 쉬우나 완벽히 복원시키는 것은 불가능에 가깝다. 이 링크는 깨진 도자기를 복원하는 Youtube 영상이다. 영상에서는 깨진 도자기의 파편들을 프레임으로 고정시키고 테이프, 레진을 사용해 접착 후 찰흙같은 것으로 공백부분을 메우며 붓으로 원래 색상과 비슷한 색상으로 덧칠하며 마무리한다. 이 처럼 깨진 도자기를 복원하는 것은 굉장히 많은 노력(에너지)을 필요로한다.

Diffusion 모델의 Reverse Process 도 마찬가지다. 완벽히 복원하는 것은 불가능하고 원본과 유사한 이미지로 복원하는 것이다. 또한 Forward Process 보다 Reverse Process 에서 더 많은 연산(에너지)을 필요로 한다.

3. 확률적 관점

이 글을 시작하는데 앞서 엔트로피는 가장 높은 확률로 나아가려는 경향성을 갖는다고 했다. 이 경향성이라는 것은 바로 앞에 일어난 사건에 영향을 받는다.

예를 하나 들어보자. 200m 거리를 두고 궁수와 과녁이 있다. 과녁의 정중앙에는 화살이 하나 꽂혀있다. 그 화살은 정중앙의 과녁에 꽂히기 전 과녁을 향해 포물선을 그리며 날아왔을 것이다. 그 포물선을 그리기 전에는 궁수가 활의 시위를 당겼을 것이며 활의 시위를 당기기 전에는 궁수가 화살을 화살통에서 꺼냈을 것이다. 굉장히 자연스러운 현상이다. 궁수가 활의 시위를 당기지도 않았는데 화살이 포물선으로 날아갈 수 없고, 화살이 과녁을 향해 나아가지도 않았는데 갑자기 화살이 과녁에 꽂혀있을 수는 없다. 영화 테넷도 아니고 이 것은 굉장히 부자연스럽다. 아래는 영화 테넷에서 시체가 갑자기 일어나서 총맞는 장면이다

위의 궁수와 과녁 예시에서 자연스러운 현상에 대한 부분은 Markov property (마르코프 성질)를 갖는다고 표현할 수 있다. Markov property 란 상태($S$)와 시점($t$)에 대해 $S_{t+1}$ 의 데이터는 $S_{t}$ 에 의존한다는 것이다. 즉, 바로 이전 시점에 의존한다는 말이다. 또한 Markov property 를 만족하면서 시간에 따라 연속적인 상태 전이가 이루어지는 것을 Markov Chain 이라고 부른다. 따라서 위의 궁수와 과녁예시는 "Markov Chain을 만족한다" 라고도 표현할 수 있다.

위의 Markov property 와 Markov Chain 을 조금 더 자세히 설명하자면, 일어난 사건에 대해 바로 앞 시점이 확률적으로 가장 많은 영향을 주고, 시점이 멀 수록 덜 영향을 준다고 할 수 있다. Diffusion Model 은 이 Markov chain 을 갖는다