
이 책으로 코테 준비해보려고 함니다..
파팅
📢 1) 배열과 리스트
(1) 배열의 개념 및 특징
배열이란 ? 메모리의 연속공간에 값이 채워져있는 형태의 자료구조
- 인덱스를 사용하여 값에 바로 접근할 수 있다.
- 새로운 값을 삽입하거나 특정 인덱스에 있는 값을 삭제하기 어렵다.
- 배열의 크기는 선언할 때 지정할 수 있으며 한 번 선언하면 크기를 늘리거나 줄일 수 없다
(2) 리스트의 개념 및 특징
리스트란? 값과 포인터를 묶은 노드라는 것을 포인터로 연결한 자료구조
-
인덱스가 없으므로 값에 접근하려면 Head부터 순서대로 접근 (속도가 느리다)
-
포인터로 연결되어 있어 데이터를 삽입하거나 삭제하는 연산 속도가 빠르다
-
선언할 때 크기를 별도로 지정하지 않아도 된다. (크기 변하기 쉬운 데이터 사용할 때 적절)
-
포인터를 저장할 공간이 필요하므로 배열보다 구조가 복잡하다
문제 1. 백준 11720번 숫자의 합 구하기
🔎 접근법 : N의 버위가 1부터 100까지니까 숫자형으로 담을 수 없다
그러니 문자열로 입력값을 받고 문자로 바꿔준 뒤, 숫자로 바꿔 계산 -
문자열 -> 문자형 : toCharArray / 문자형 -> 문자열 : String.valueOf
-
문자열 입력 받을땐 next() 함수 사용
import java.util.Scanner; class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); // 첫 번째 입력: 숫자의 개수 int N = sc.nextInt(); // 두 번째 입력: 숫자 문자열 String sNum = sc.next(); char[] cNum = sNum.toCharArray(); // 문자로 바꿔 주기 int sum = 0; for(int i = 0; i < cNum.length; i++) { sum += cNum[i] - '0'; } System.out.println(sum); } }
아스키코드에서 같은 의미의 문자의 숫자 코드 값 차이는 48이다
'1'- 48 또는 '1'-0 의 형식으로 변환
문제2. 백준 1546번 평균 구하기
🔎 접근법
변환 점수 평균 구하는 법 > ( A + B + C ) * 100 / 최댓값 / 3
import java.util.Scanner;
class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// 1. 전체 과목 수 받아오기 + 선언
int total = sc.nextInt();
int [] score = new int[total]; // 이 부분
// 2. 점수 받아오기 + 최대값 구하기 + 총합 구하기
long max = 0;
long scoreSum = 0;
for (int i = 0; i < total; i++) {
score[i] = sc.nextInt();
if(max < score[i]) {
max = score[i];
}
scoreSum += score[i];
}
System.out.println(scoreSum * 100.0 / max / total);
}여기서 굳이 long을 사용한 이유는 total의 크기가 1000까지라고 해서 사용함
📢 2) 구간 합
(1) 합 배열 S 정의
S[i] = A[0] + A[1] + A[2] + ... + A[i-1] + A[i]
기존 배열의 일정 범위의 합을 구하는 시간 복잡도가 O(N)에서 O(1)로 감소
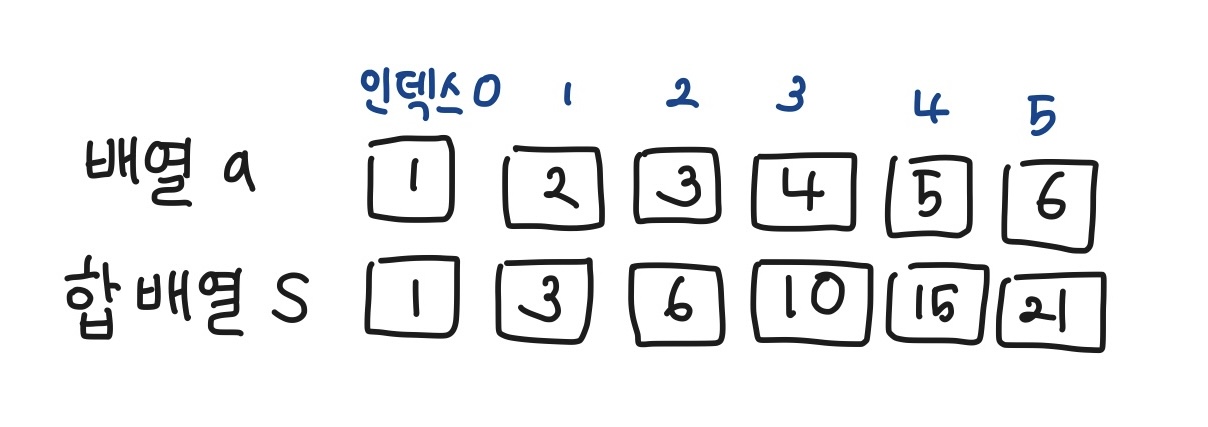
(2) 합 배열 S를 만드는 공식
S[i] = S[i-1] + A[i]
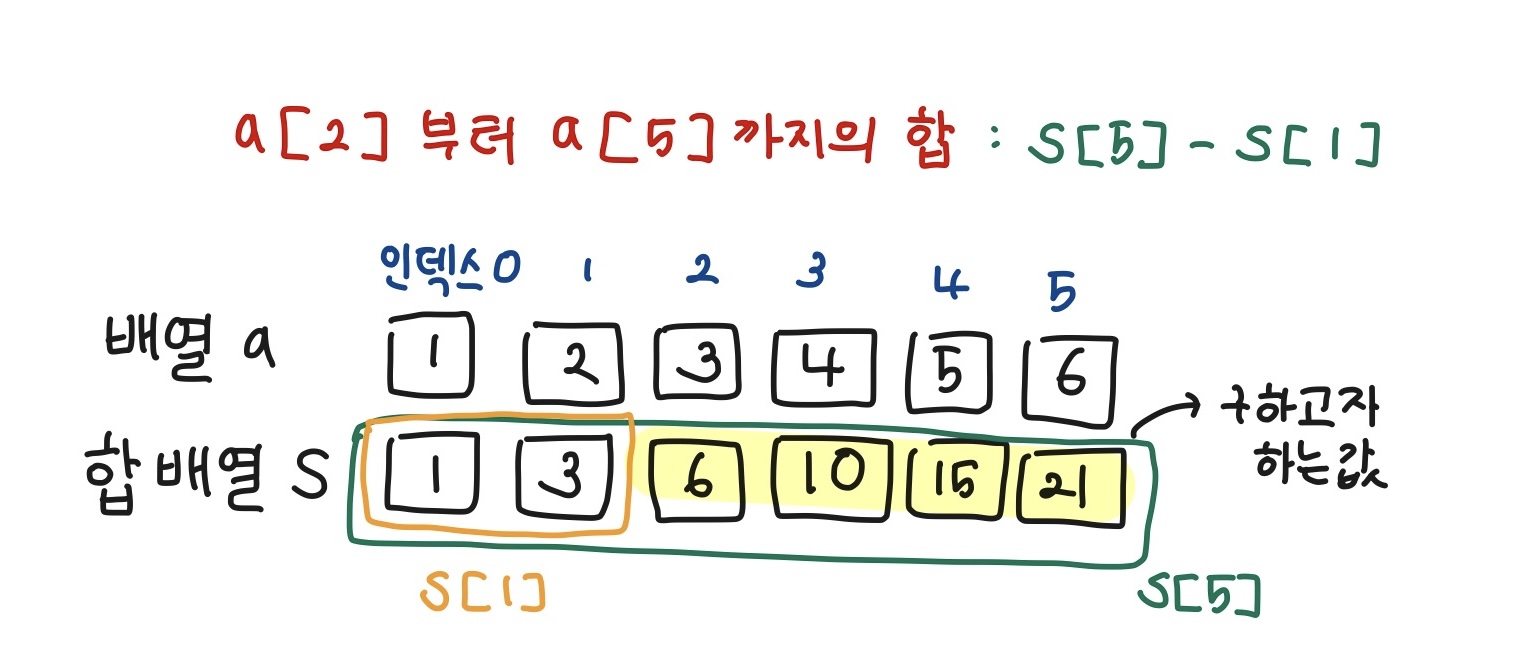
(3) 구간 합 구하는 공식
S[j] - S[i-1] : i에서 j까지 구간 합
문제 1. 백준 11659번 구간 합 구하기
🔎 접근법 :
1. BufferedReader가 Scanner보다 빠르다
2. StringTokenizer로 문자열을 구분하여 각 입력 줄을 따로 사용하자
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class rangeSum1 {
public static void main(String[] args) throws IOException {
// 백준 11659번 구간 합 구하기
BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); // 사용자 입력 받기
StringTokenizer line1 = new StringTokenizer(br.readLine()); // 문자열 분리
// 1. 개수 정하기
int nData = Integer.parseInt(line1.nextToken());
int nQuiz = Integer.parseInt(line1.nextToken());
// 2. 부분 합 배열 만들기
long [] sArr = new long[nData + 1]; // sArr[0] = 0으로 초기화
StringTokenizer line2 = new StringTokenizer(br.readLine());
for(int i = 1; i <= nData; i++) {
sArr[i] = sArr[i-1] + Integer.parseInt(line2.nextToken());
}
// 3. 질의 세 개 만들고 계산하기
for(int i = 0; i < nQuiz; i++) {
StringTokenizer line3 = new StringTokenizer(br.readLine()); // 질의를 반복해야 하니까 for문 안에 입력
int q1 = Integer.parseInt(line3.nextToken());
int q2 = Integer.parseInt(line3.nextToken());
System.out.println(sArr[q2] - sArr[q1-1]);
}
}
}문제 2. 백준 11660번 구간 합 구하기
🔎 접근법
1. 2차원 배열 합 배열 활용
이차원 배열 선언하는 법
int[][] a = new int[n][n]
- 이차원 배열 구간합 구하는 법
dArr[i][j] = dArr[i][j-1] + dArr[i-1][j] - dArr[i-1][j-1] + sArr[i][j]
- 이차원 배열 부분합 구하는 법
dArr[x2][y2] - dArr[x1-1][y2] - dArr[x2][y1-1] + dArr[x1-1][y1-1]import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; import java.util.StringTokenizer;
public class rangeSum2 {
public static void main(String[] args) throws IOException {
/ 백준 11660번 구간 합 구하기 /
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer line1 = new StringTokenizer(br.readLine());
// 1. 배열 사이즈, 질의 개수
int nSize = Integer.parseInt(line1.nextToken());
int nQize = Integer.parseInt(line1.nextToken());
// 2. 2차원 배열 만들기
int [][] sArr = new int[nSize + 1][nSize + 1]; // sArr[0] = 0
for(int i = 1; i <= nSize; i++) {
StringTokenizer line2 = new StringTokenizer(br.readLine());
for(int j = 1; j <= nSize; j++) {
sArr[i][j] = Integer.parseInt(line2.nextToken());
}
}
// 3. 구간합 구하기
int [][] dArr = new int[nSize + 1][nSize + 1];
for(int i = 1; i <= nSize; i++) {
for(int j = 1; j <= nSize; j++) {
dArr[i][j] = dArr[i][j-1] + dArr[i-1][j] - dArr[i-1][j-1] + sArr[i][j];
}
}
// 4. 질의
for(int i = 0; i < nQize; i++) {
StringTokenizer line3 = new StringTokenizer(br.readLine());
int x1 = Integer.parseInt(line3.nextToken());
int y1 = Integer.parseInt(line3.nextToken());
int x2 = Integer.parseInt(line3.nextToken());
int y2 = Integer.parseInt(line3.nextToken());
System.out.println(dArr[x2][y2] - dArr[x1-1][y2] - dArr[x2][y1-1] + dArr[x1-1][y1-1]);
}
}}
