🔍 KMP 알고리즘이란?
Knuth-Morris-Pratt 알고리즘의 약자로, 효율적인 문자열 검색을 위한 알고리즘이다. 주어진 텍스트에서 특정 패턴을 찾을 때, 이미 검사한 부분을 반복하지 않고도 빠르게 검색을 수행하며 n이 텍스트의 길이, m이 패턴의 길이 일 때, 의 시간복잡도를 자랑합니다.
⚔️ 문자열 검색 알고리즘 - 브루트 포스와의 차이
일반적인 문자열 검색 알고리즘(예 : 브루트 포스)은 불일치가 발생하면 패턴을 한 칸씩 옮겨가며 처음부터 다시 비교합니다. 그러나 KMP 알고리즘은 패턴 내에서의 접두사와 접미사의 일치 정보를 활용하여 불필요한 비교를 줄입니다.
📊 부분 일치 테이블 (PSL, Partial Match Table) 생성 과정
부분 일치 테이블은 패턴의 각 위치에서 접두사와 접미사가 얼마나 일치하는지를 나타냅니다. 이 테이블은 검색 과정에서 패턴을 얼마나 이동시킬지 결하는 데 사용됩니다. Pi 테이블나 실패 함수(Failure Function)이라고도 불립니다.
table의 값은 주어진 문자열의 0~i까지의 부분 문자열 중에서 prefix==suffix가 될 수 있는 부분 문자열 중에서 가장 긴 것의 길이를 구합니다.
예를 들면 "ABAABAB"의 PSL을 구하면 다음과 같다.
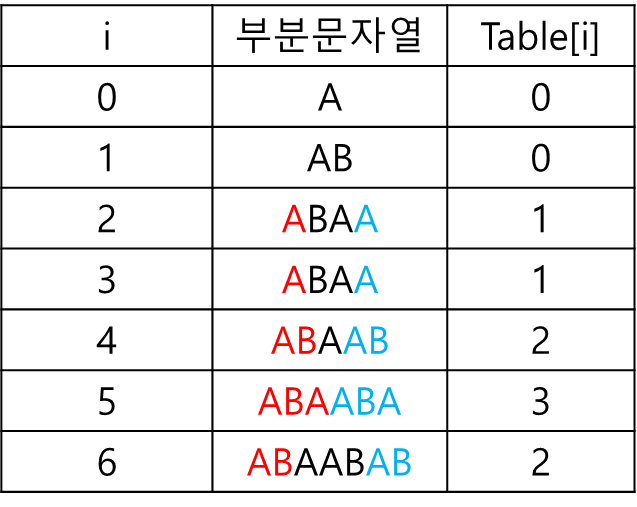
먼저 코드부터 보면 다음과 같다.
def create_pi_table(pattern):
table=[0 for _ in range(len(pattern))]
i=0
for j in range(1,len(pattern)):
while i>0 and pattern[i]!=pattern[j]:
i=table[i-1]
if pattern[i]==pattern[j]:
i+=1
table[j]=i
return tablej는 자동으로 +1씩 증가하기 때문에 이를 인지하면서 다음의 상황을 확인하면 된다.
i는 앞에서부터 확인하는(접두사를 확인하는) 인덱스이고 j는 뒤에 있는 접미사를 확인하는 인덱스이다.
만약 현재 확인해 나가고 있는 각 접두사와 접미사의 새로운 부분이 같다면 즉, pattern[i]==pattern[j]라면 현재까지가 j번째 인덱스까지 확인했을 때의 PSL의 값이 되므로 table[j]에 i값을 넣어준다. 여기서 i는 접두사의 길이이기 때문에 최대 길이의 값과 같다고 할 수 있다. 그런 다음 i와 j가 다음값의 확인을 위해 늘어나는 것이다.
현재 진행한 i가 즉 접두사의 길이가 0보다 큰 상태에서 pattern[i]!=pattern[j]라면 즉, 새롭게 확인할 접두사와 접미사의 문자가 다르다면 보장상태가 유지될 때까지 i를 갱신한다.
이 때, 같은거까지의 상태를 보장하는 것을 이용하는 것이다. 즉, 같은부분이었던 곳까지 이동하고 그 뒤에부터는 다시 확인하는 것이다.
보장성의 확인은 다음과 같다.

동그라미와 세모가 각 다른 문자가 나왔을 때, table[j-1] = N이라면, 즉 j-1까지의 문자열에서 접두사와 접미사의 공통된 최대 길이가 N개이다.
이때 i의 인덱스는 접두사의 다음 인덱스 이므로 N이라고 할 수 있다.
따라서 i=table[j-1]이라고 할 수 있다.
똑같은 과정으로 N 내부에서도 다음과 같이 따질 수 있다.

table[i-1] = M이라면 위의 그림처럼 초록색으로 칠해진 두 부분이 서로 같다는 뜻이다. 즉, i-1까지의 문자열에서 같은 부분의 길이가 M이라는 것이다.
위의 그림 두 개를 연관지어 생각해 본다면 초록색 부분이 똑같이 뒤에 있는 파란색 부분에도 똑같이 나타나므로 값들을 똑같이 적용시킬 수 있다.
결국 앞에 있는 M개와 맨 뒤에 있는 M개에 한해서 같다는 것이 보장이 되기 때문에 다음 i, 즉 접두사를 늘려갈 부분을 table[i-1]부터 따질 수 있다. 이 때 보장성을 추적하면서 찾아갈 때, 다른 글자가 나올 수 있기에 같을 때까지 반복해서 찾아들어가는 것이다. 그래서 while문으로 동작한다.
🧩 PSL을 활용한 KMP 알고리즘 구현
PSL을 구하는 방식과 유사하다고 볼 수 있다.
먼저 코드를 보면 다음과 같다.
def kmp(all_string,pattern):
table=create_pi_table(pattern)
# kmp
i=0
result=[]
for j in range(len(all_string)):
while i>0 and pattern[i]!=all_string[j]:
i=table[i-1]
if pattern[i]==all_string[j]:
i+=1
if i==len(pattern):
result.append(j-i+2)
i=table[i-1]
return result전체 문자열을 나타내는 all_string과 패턴을 나타내는 pattern이 존재할 때, 각 검사하는 인덱스를 i와 j로 둔다.
만약 각 문자열에서 i와 j가 나타내는 글자가 같다면 j는 자동으로 이동하고 있기 때문에 한번 더 다음문자까지 같은지 확인해야 하므로 각 i와 j를 1씩 증가시킨다. 이 때, i가 pattern의 길이까지 진행했다면 패턴이 일치하는 부분이므로 해당 인덱스를 답으로 내보낸다. 그리고 공통된 부분으로 보장되는 부분부터 다시 i를 탐색하는 것이다.
만약 같지 않다면 어차피 새롭게 탑색해야 하는데 아까 구해놓은 PSL을 위해 보장된 공통된 부분을 건너뛰고 i를 PSL을 구할 때와 마찬가지로 갱신하면 된다.
⭐ PSL의 활용 - 최소 패턴 파악
PSL의 활용 방법 중 하나는 반복되는 최소 패턴을 파악할 수 있다는 것이다. 직관적으로 생각해보자. 접두사와 접미사의 반복되는 패턴을 제외한 나머지 부분을 보면 된다.

색칠된 접미사 부분이 뒤쪽에 오기 때문에 접미사 부분에도 이 패턴이 반복된다. 그리고 이 패턴의 끝은 접미사 부분의 바로 앞 부분인 해당 그림에서는 색칠된 A 앞에 오는 B이기 때문에 해당 패턴의 끝이 된다고 이해할 수 있다.
그렇기에 최소 패턴의 길이는 전체 길이인 N에서 패턴의 길이를 뺀 것이 반복되는 최소 패턴의 길이라고 할 수 있다. 이다.

