[게임 수학] 원근 투영 보정

🧐 해당 파트는 게임 개발 환경을 구성하는 컴퓨터 그래픽스(Computer Graphics)를 이해하기 위한 기초 수학의 간단한 개념에 대해 설명하고 있습니다!

혹여나 이해가 잘 안되거나 잘못된 정보를 발견하시게 되었다면 관련해서 피드백 해주시면 정말 감사하겠습니다!

❗ 이번 파트는 무게중심좌표의 개념을 알고있다는 가정 하에 진행됩니다!
기회가 된다면 무게중심좌표에 대해서도 이야기 하도록 하겠습니다.

OpenGL SuperBible 책에서 언급된 원근투영보정입니다.
이곳엔 원리가 생략되었기 때문에 큰 생각 없이 그냥 자연스럽게 넘어갔었다가 수식을 보고 크게 놀랐었습니다.

왜냐하면 '아 그래픽 라이브러리가 알아서 처리해줍니다~'느낌으로 진행되어서 그냥 단순계산이 많은가보다 생각했지만 원근투영보정이 꽤 복잡한 원리로 돌아갈 줄은 상상도 못했기 때문입니다...

혼돈으로 몰아넣은 원근 투영 보정... 한번 알아보겠습니다...!

1.원근 투영 보정을 왜 하나요?

이전까지는 깊이값도 포함된 원근투영을 모두 배웠고 적용도 할 수 있게 되었습니다! 신난다!
그런데 막상 적용하고 돌려보니 위 이미지의 순수 아핀 공간에서 보여지는 형태로 렌더링이 됩니다.
어찌보면 종이가 접혀있는 느낌의 착시도 느껴집니다.

사실 저도 OpenGL을 통해 리듬게임을 만들 때 이런 현상이 나타나 당황했었지만
텍스쳐에 파라미터값을 몇개 넣어주니 해결됐었던 기억이 납니다!

그리고 원근 투영 보정의 게임 그래픽스의 역사는 생각보다 오래되지 않았습니다.
대표적인 예시로 PS1시절 게임들은 해당 현상을 그대로 놔뒀던 것을 볼 수 있습니다.
아마 당시 하드웨어 제약으로 인해 이러한 텍스쳐 보간이 힘들었던 것으로 생각됩니다.

그래서 요즘 PS1 에뮬레이터들은 해당 문제점을 보간하는 파이프라인을 도입하여 해당 현상을 수정하였습니다. (해당 설명의 출처 : https://www.ngemu.com/threads/pcsxr-pgxp.186369/)

흠... 그나저나 왜 이런 현상이 일어날까요?

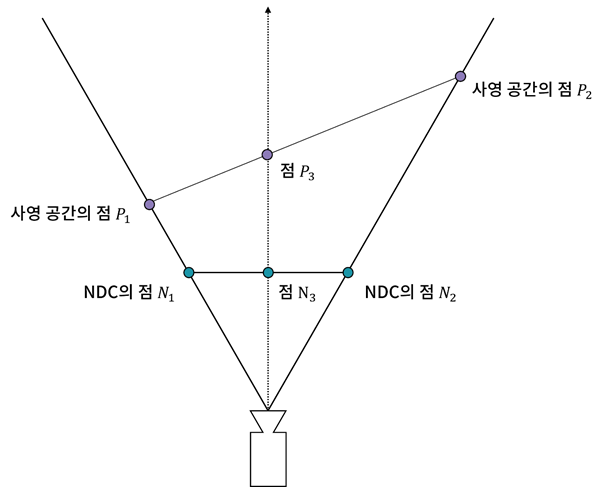
사실 원근투영공간(사영공간)을 통해 변환된 무게중심좌표는 위 보라색의 점처럼 나타낼 수 없습니다.
왜냐하면 깊이값이 선형의 형태가 아닌 저번에 봤던 $\log$의 그래프 형태로 나타나기 때문입니다.

이를 다시 정리하자면 무게중심좌표가 선형 공간에 포함된 무게중심좌표가 아니기 때문에 이런 문제가 발생한다고 합니다.

이런 현상을 개선하기 위해선 선형 공간에 포함된 깊이값을 얻어야 하는데
개선하는 방법은 바로 뷰공간 기준으로 다시 얻어와서 보간을 진행해야합니다.

관련하여 필요한 수식은 아래와 같이 정리하였습니다.

1-1. 원근 투영 보정 수식 맛보기

💡 해당 파트는 수식을 정리하는 것에 집중합니다.
이 수식에 대한 상세한 유도과정은 아래에서 확인할 수 있습니다!

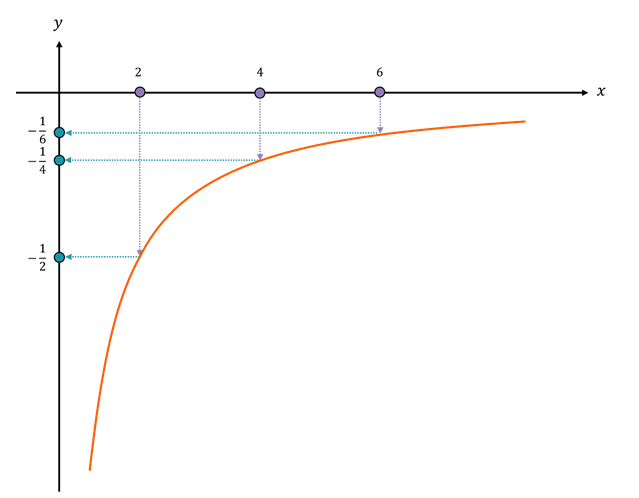
무작정 NDC 공간으로 다시 얻어오는 과정은 생각보다 쉽지 않습니다. 앞서말한 깊이값이 선형이 아니기 때문입니다. 따라서 위의 그림처럼 일정한 간격의 위치값($x$)과 깊이맵을 통해 변형된 위치값($y$)의 비율이 아래의 그림처럼 달라지는 문제가 존재합니다.

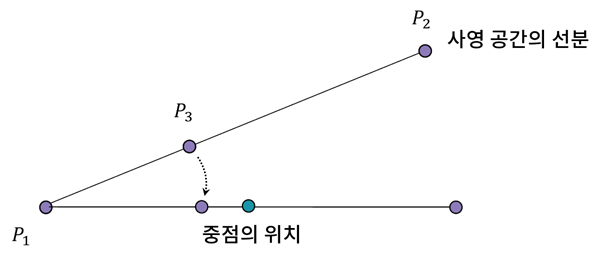
그대로 되돌려서 쓰는 방식은 못쓸 것 같습니다..
그러니 저희는 다른 수식을 통해 원근 투영 보정을 진행하고자 합니다.

일단 $t_1, t_2, t_3$는 뷰공간에서의 무게중심좌표,
$q_1, q_2, q_3$는 NDC를 통해 투영되어 나온 무게중심좌표라 선언하고 수식을 풀어보겠습니다.

먼저 사영공간에서 NDC 공간으로 되돌리기 위해 $y = -\frac{1}{x}$성질을 이용하여 투영되기 전 무게중심좌표를 만듭니다. 해당 과정을 통하여 $x'$을 만듭니다.

$t_1, t_2$도 위와 같은 성질로 $t_1 \cdot x_1 + t_2 \cdot x_2 = x'$ 의 식을 얻을 수 있으며 여기서 하나의 축을 추가하여 아래와 같은 수식으로 구할 수 있습니다.

여기서 $x$축을 $z$축으로 변경하여 사영공간의 점과 곱하여 올바른 깊이값을 얻을 수 있는 $z'$을 구할 수 있습니다.

간단하게 수식을 구하는 단계와 수식의 결과를 확인했지만 이걸론 이해하기 힘들 수 있습니다.
저도 그랬으니깐요! 그러니 아래에 있는 상세한 유도과정을 확인해주시면 감사하겠습니다.

2. 원근 투영 보정 수식

위에선 보정하는 단계와 간단한 수식만으로 작성되었으니 이번엔 한번 저 수식을 유도해보는 과정을 작성해보고자 합니다.

일단 어느 한 점이 삼각형의 매쉬에 존재하는지 판단하고 이를 비율값으로 얻어올 수 있습니다.
이것이 우리가 흔히 말하는 UV좌표이며, 텍스쳐 렌더링에 꼭 필요한 존재입니다.

어쨌든 3개의 점으로 구성된 삼각형에 점 $P'$를 구하는 공식은 아래와 같습니다.

이전부터 무게중심좌표를 알고계신 분들은 익숙하실 식입니다!

무게중심좌표의 개념을 잘 모르시는 분들을 위해 이 개념과 관련하여 반드시 짚고 넘어가야 할 내용을 간단하게 다뤄보도록 하겠습니다.

무게중심좌표의 합은 왜 항상 $1$일까?
아핀공간에서 점과 점을 더해 새로운 점을 만드는 결합식의 기본조건이 되기 때문입니다.
이 이외에도 해당 공간에서 계산을 위해 실질적인 기준을 잡아줘야하는 부분도 있는데 이를 편리하게 연산할 수 있도록 1로 설정한 이유도 있습니다.

그렇다면 위 내용을 원근투영보정에 적용한다면 무게중심좌표를 통해 점 $P'$을 구하는건데
그대로 적용하기엔 깊이값에 문제가 있으니 뷰공간의 깊이값을 통해 사영공간 내에서 정상적인 깊이값을 표현해주는 $z'$을 구하는 것이라고 보면 될 것 같습니다!

이번 파트는 수식을 유도하는 과정이니 위의 $P'$의 수식을 통해 유도해보도록 하겠습니다.
먼저 저 수식을 사영공간에 있는 깊이값인 $z'_{per}$과 함께 아래와 같이 표현하였습니다.

여기서 뷰좌표의 깊이를 알아내기 위해 $z'_{per}$를 투영되기 전 단계의 깊이값에 반비례한 성질을 뷰좌표의 깊이값인 $z'$으로 다음과 같이 표현할 수 있습니다.

사실 위에서 다뤘던 원근투영보정의 수식을 유도했기 때문에
이번엔 거꾸로 이 수식에서 뷰공간의 무게중심좌표인 $t_1, t_2, t_3$값을 유도하여 수식이 맞는지 알아보도록 하겠습니다.

유도하는 방식은 무게중심좌표들의 합이 1인 성질을 통해 뷰공간의 무게중심좌표들과 서로 비교하며 수식을 유도할 생각입니다.

따라서 한쪽에 $1$만 남기도록 수식을 다시 정리합니다.

뷰공간의 무게중심좌표인 $t_1, t_2, t_3$를 가지고 한쪽에 1만 남은 식을 표현해줍니다.
이미 뷰공간에 존재하는 무게중심좌표이기 때문에 특별한 변환없이 아래와 같이 나타납니다.

이제 두 수식은 합쳐서 서로 동등한 형식을 지니도록 만들어줍니다.

여기서 서로 같은 무게중심좌표라는 점에서 아래와 같이 뷰공간의 무게중심좌표 수식을 유도할 수 있었습니다.

수식을 다시 거슬러 올라가며 뷰공간의 무게중심좌표를 좀 상세히 유도하는 과정을 진행해봤습니다.
개인적으론 처음 수식을 유도할 때 햇갈렸지만 거꾸로 다시 무게중심좌표를 유도해보니 이해가 되었기 때문에 이와 같이 진행을 해봤습니다!

다음장은 절두체(Frustum)를 알아보기 위해 평면의 방정식을 다루도록 하겠습니다.