미리보기
👀트리 구조
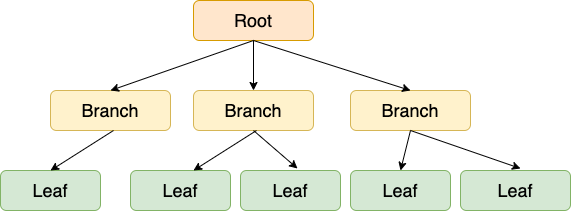
가장 상단의 노드를 '루트 노드(Root Node)',
중간 노드들을 '브랜치 노드(Branch Node)',
가장 아래 노드들을 '리프 노드(Leaf Node)'이다.
🌳B Tree VS B+Tree
| B Tree | B+Tree | |
|---|---|---|
| 데이터 저장 | 브랜치노드, 리프노드 | 리프노드에만 데이터 저장 |
| 트리의 높이 | 높음 | 낮음 (한 노드당 KEY를 많이 가질 수 있음) |
| 풀스캔 | 모든 노드 탐색 | 리프노드에서 선형 탐색 |
| 키중복 | 없음 | 있음 (리프노드에만 데이터가 있기 때문) |
| 검색 | 자주 access 되는 노드를 루트 노드 가까이 배치할 수 있고, 루트 노드에서 가까울 경우, 브랜치 노드에도 데이터가 존재하기 때문에 빠름 | 리프노드까지 가야 데이터 존재 |
| Linked List | 없음 | 리프 노드끼리 Linked List로 연결 |
✨트리는 어디에 속하는가!
이진트리(Binary Tree)에는 정이진트리(Full binary tree), 포화이진트리(Perfect binary tree), 완전이진트리(Complete binary tree), 균형이진트리(Balanced binary tree) 등이 있다. 그 중 균형이진트리는 리프 노드들의 레벨차이가 최대 1레벨까지만 나는 트리를 뜻한다.
-> 균형이진트리는 AVL 트리, 레드블랙 트리, B-Tree, B+Tree, B*Tree 등에서 주로 사용된다. B Tree와 B+Tree는 균형이진트리이기 때문에 리프노드가 같은 레벨에 유지되도록 자동으로 밸런스를 맞춘다
B Tree
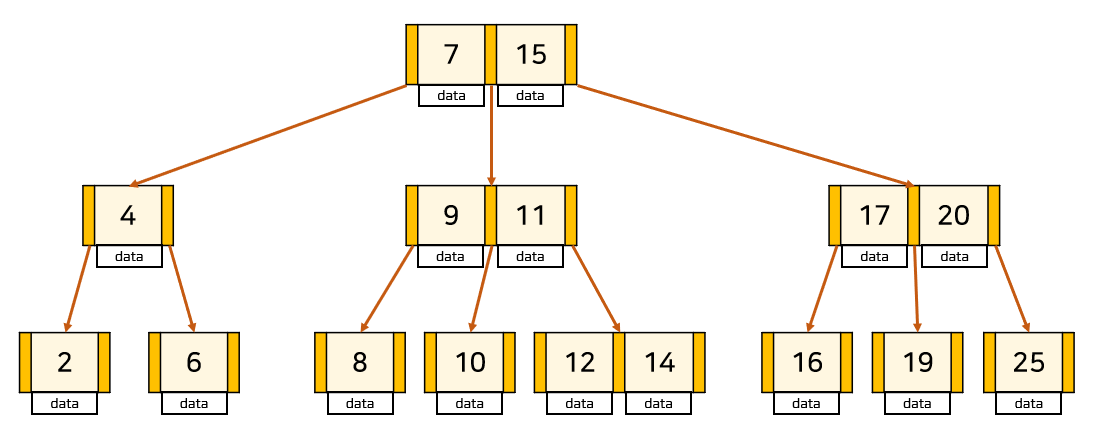
- 노란색 부분은 각 노드의 key를 나타내며, 주황색 부분은 자식 노드들을 가르키는 포인터이다.
- 이진 트리와는 다르게, 하나의 노드에 많은 정보를 가지거나, 두 개 이상의 자식을 가질 수도 있다.
- 최대 M개의 자식을 가질 수 있는 B-Tree를 M차 B-Tree : [사진 예시] : 3차 B-Tree (4/9,11/17,20)
- 노드는 최대 M개 부터 M/2개 까지의 자식을 가질 수 있다. : [사진 예시] : 1~3개의 자식
- 노드에는 최대 M−1개 부터 [M/2]−1개의 키가 포함될 수 있다. :
[사진 예시] : 2~0개의 키
(만약 하나에 3개의 노드가 있다면 2개의 키가 존재하고 1개의 노드만 있다면 키가 필요 없다) - 노드의 키가 x개라면 자식의 수는 x+1개 이다.
- 최소차수는 자식수의 하한값을 의미하며, 최소차수가 t라면 M=2t−1을 만족한다. (최소차수 t가 2라면 3차 B트리이며, key의 하한은 1개이다.)
B Tree를 사용하는 이유
탐색에 용이하기 때문이다!
풀 스캔은 비례 형태로 실행 시간이 늘어가는데에 비해,
인덱스를 사용한 경우 실행 시간의 저하는 보통 원만한 곡선을 그리게 된다.
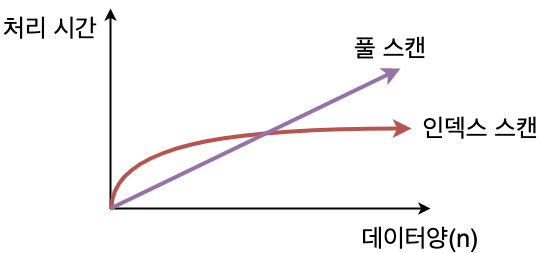
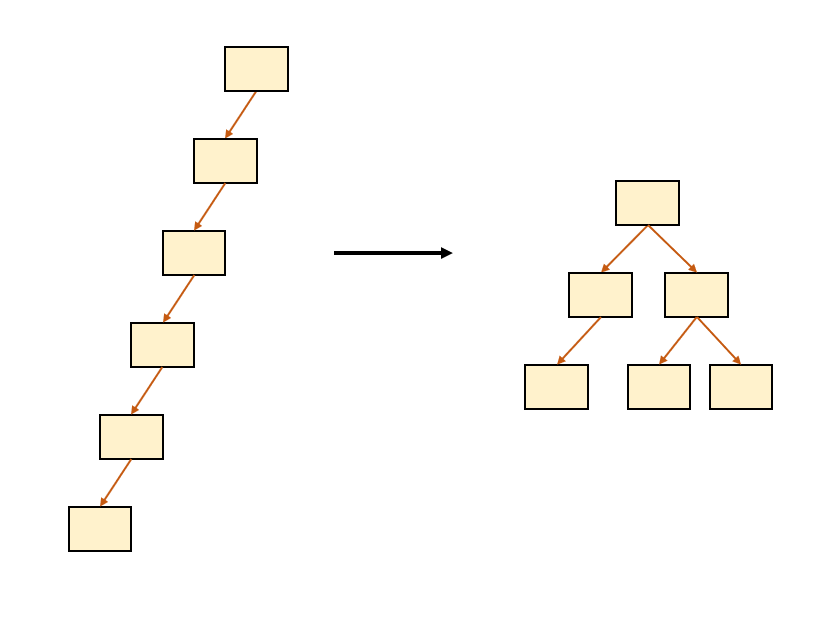
즉, 발란스를 유지하면 최악의 경우에도 O(logN)의 시간이 보장된다. 트리가 편향된 경우 최악의 시간복잡도로 O(N)을 갖게 된다.
B+Tree
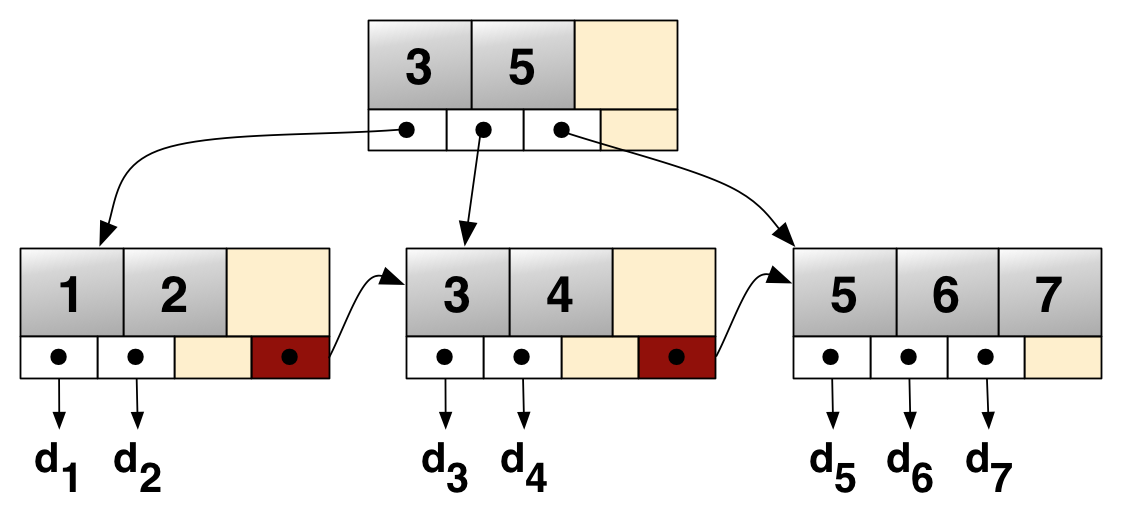
- B+tree는 B-tree의 확장개념이다
- B-tree의 경우, 브랜치 노드에 key와 data를 담을 수 있다.
하지만, B+tree의 경우 브랜치 노드에 key만 담아두고, data는 담지 않는다. - 오직 리프 노드에만 key와 data를 저장하고, 리프 노드끼리 Linked list로 연결되어 있다.
B+ Tree를 사용하는 이유
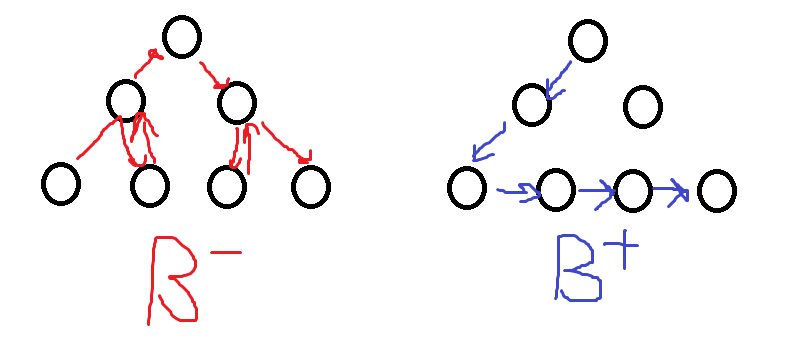
- B+ Tree는 리프 노드를 제외하고 데이터를 담아두지 않기 때문에 메모리를 더 확보한다. 따라서 더 많은 key들을 수용한다. 하나의 노드에 더 많은 key들을 담을 수 있기에 트리의 높이는 더 낮아진다.
- B+tree는 리프 노드에 데이터가 모두 있기 때문에 풀스캔시 한 번의 선형탐색만 하면 되기 때문에 B-tree에 비해 빠르다. 반면, B-tree의 경우에는 모든 노드를 확인해야 한다.
참고자료
1) https://zorba91.tistory.com/293
2) https://ssocoit.tistory.com/217
3) https://toward-the-future.tistory.com/entry/%EC%9E%90%EB%A3%8C-%EA%B5%AC%EC%A1%B0-2-%ED%8A%B8%EB%A6%ACTree-%EC%9D%B4%EC%A7%84-%ED%83%90%EC%83%89-%ED%8A%B8%EB%A6%ACBinary-Search-Tree-%EA%B7%A0%ED%98%95-%EC%9D%B4%EC%A7%84-%ED%83%90%EC%83%89-%ED%8A%B8%EB%A6%ACBalanced-Binary-Search-Tree-AVL-%ED%8A%B8%EB%A6%AC
4) https://rebro.kr/169