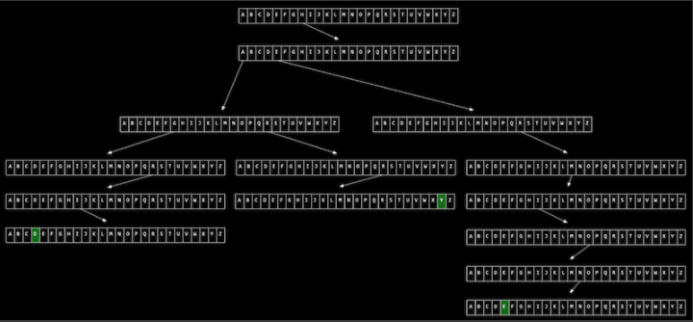
트라이(Trie)란?
이진 검색 트리 등에서는 원소를 찾는데 O(logN)의 시간이 걸리게 된다.
하지만 문자'열'의 경우 두 문자열을 비교해야 하는데, 이때는 문자열의 길이만큼 시간이 걸린다. 원하는 문자열(M개)을 찾기 위해서는 O(MlogN)의 시간이 걸리게 된다.
이 단점을 해결하기 위한 특화된 자료구조가 트라이(Trie)이다.(문자열 특화)
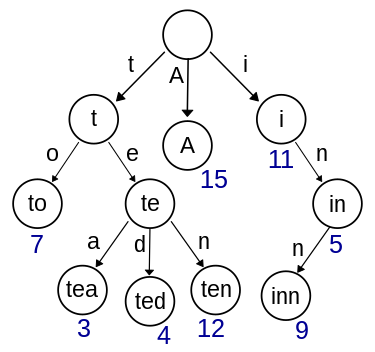
- 트라이(Trie)는 탐색 트리의 일종이다.
re'trie'val tree에서 나온 단어이다. - 트라이(Trie)는 문자열을 저장하고 효율적으로 탐색하는데 특화되어 있다.
- 트라이는 문자열이 키인 경우가 흔하지만, 꼭 그래야 하는 것은 아니다. 숫자나 도형의 리스트로 구성한 순열 같은 것이 가능하다.
- 자동완성 기능, 사전 검색 등에 쓰인다.
트라이(Trie) 장단점
장점
- 하나하나씩 전부 비교하면서 탐색을 하는 것보다 시간 복잡도 측면에서 훨씬 더 효율적이다.
트라이(Trie)는 문자열을 추가하는 경우에 문자열의 길이만큼 노드를 따라가거나, 추가하면 되기 때문에 문자열의 추가와 탐색이 모두 O(M)만에 가능하다.
- 트라이에서는 해시함수를 이용하는 해시트리 처럼 키 충돌이 일어나지 않는다.
- 여러 값이 하나의 키와 연관되어 있지 않는 한 버킷이 필요 없다.
- 해시 함수가 없어도 된다.
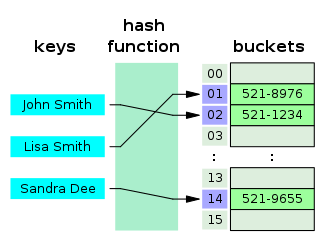
참고: [해시테이블 추가 설명]
단점
- 저장 공간의 크기가 크다
-> 각 노드에서 자식들에 대한 포인터들을 배열로 모두 저장하고 있다
만약 사전 검색을 할 때, 알파벳이 모두 필요하다.
문자열이 모두 알파벳 소문자로만 이루어진 경우라고 해도, 1 depth에 a~z까지 26개의 공간이 필요하게 된다.
1. 이 단점을 해결하기 위해 보통 map이나 vector를 이용하여 필요한 노드만 메모리를 할당하는 방식들을 이용한다.
2. 각 키마다 부가적인 정보를 저장하는 Trie와 달리 필요가 없이 키만 저장하면 되는 경우는,
최소 결정 비순환 유한 상태 오토마타(DAFSA)가 트라이보다 적은 공간을 사용한다. DAFSA는 서로 다른 키에서 접미사를 공유하는 경우 동일한 가지를 이용하는 방식으로 압축하기 때문이다.
맞춤법 검사나 하이픈 연결 소프트웨어에 사용되는 알고리즘과 같은 근사 일치 알고리즘을 구현하는 데도 적합하다.
트라이(Trie)에서 문자 삽입

1. 트라이(Trie)에 'te' 삽입
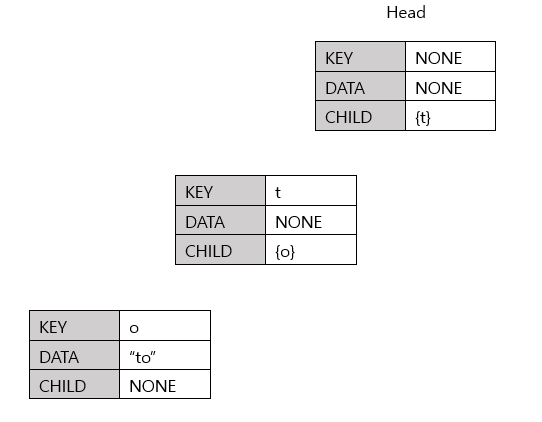
1) 첫 번째 문자는 't'이다. 초기에 트라이 자료구조 내에는 아무것도 없으므로 Head의 자식노드에 't'를 추가해준다.
2) 't'노드에도 현재 자식이 하나도 없으므로, 't'의 자식노드에 'e'를 추가해준다.
3) 'te' 단어가 여기서 끝남을 알리기 위해 o가 있는 노드의 data에 te라고 표시한다.
2. 'te' 트라이(Trie)에 'tea'삽입
1) 현재 Head의 자식노드로 't'가 이미 존재한다. 따라서 't'노드를 추가하지 않고, 기존에 있는 't'노드로 이동한다.
2) 'e'도 't'의 자식노드로 이미 존재하므로 'e'노드로 이동한다.
3) 'te' 단어는 여기서 끝이므로 DATA가 te인 노드를 두고
DATA가 tea인 노드를 만든다.
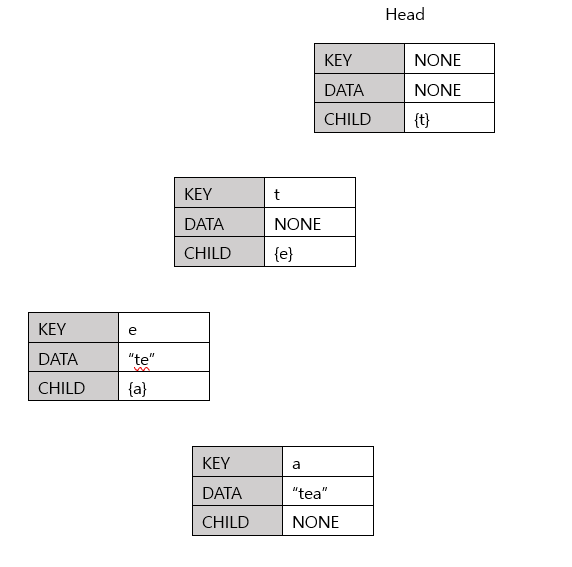
트라이(Trie)에서 문자열 탐색
위의 데이터 삽입한 것을 바탕으로 트라이에서 문자열 탐색을 해보자!
위의 트라이에 'tea' 문자열이 있는지 탐색해보기!
1) Head의 child에 't'가 존재 --> 'a'노드(key='a')로 이동
2) 't'노드의 child에 'e'가 존재 --> 'e'노드(key='e')로 이동
3) 'e'노드의 child에 'a'가 존재 --> 'a'노드(key='a')로 이동
4) 현재 노드('a'노드)에 Data값 존재(tea)
--> 따라서 'tea'라는 문자열이 존재함을 알 수 있음
참고자료
1) https://ko.wikipedia.org/wiki/%ED%8A%B8%EB%9D%BC%EC%9D%B4_(%EC%BB%B4%ED%93%A8%ED%8C%85)
2) https://velog.io/@kimdukbae/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%ED%8A%B8%EB%9D%BC%EC%9D%B4-Trie
3) https://velog.io/@klloo/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%ED%8A%B8%EB%9D%BC%EC%9D%B4Trie-%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0