시계열 데이터
시간의 흐름에 따라 관찰된 데이터 (기온 데이터, 주가 데이터 등)
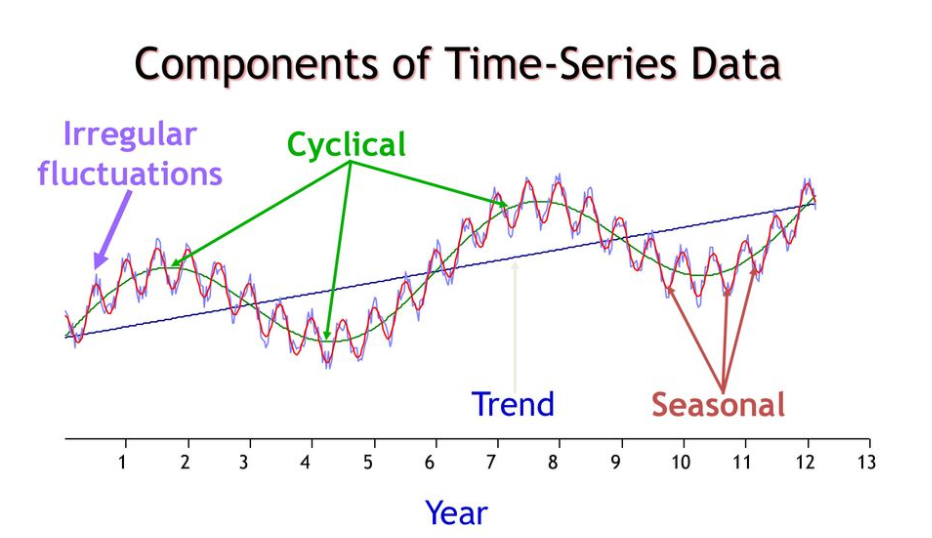
변동 요인
-추세 변동(trend): 장기간에 걸쳐 점진적이고 지속적인 상승, 하락 상태
-계절 변동(any apparent sharp changes in behavior): 주기적인 패턴을 가지고 반복적으로 나타나는 변동
-순환 변동(any apparent sharp changes in behavior): 수년간의 간격을 두고 상승과 하락이 주기적으로 나타나는 변동
-불규칙 변동(any outlying observations): 명확히 설명될 수 없는 요인에 의해 발생되는 변동(ex.코로나)
시점에 따라 평균과 분산이 일정하지 않음. 분석한 데이터에 대해 신뢰할 수 없음.
-> 시점에 따라 평균과 분산이 일정하도록 전처리 과정 필요
전처리 EDA
정상성(Stationary) :시계열 데이터가 시점에 따라 평균이나 분산이 변하지 않는 특징
평활화(Smoothing): 추세를 부드럽게 만드는 방법 -> 노이즈 제거하여 부드럽게
-이동평균법: 이전 일정한 구간의 평균
-지수평활법: 특점 시점에 가중치
--->평활화를 수행을 했을때 분산이 안정되는 느낌은 들지만, 특정 시점에 따라 데이터가 정상성을 띄긴 어려울 것이다.
차분: 현 시점의 데이터를 이전 시점의 데이터와 빼는 방법 -> 현시점-이전시점 = 그래프의 차이만 남음 -> 평균과 분산이 일정
평활화와 차분으로 정상성을 갖춘 시계열 데이터를 만듬
모델 학습
-AR
자기자신의 과거 값이 미래를 결정하는 모델
부분자기상관함수(PACF)를 활용 AR(p)모델 선정
yt = ~~~ 자기 자신의 과거값들의 합 = 미래를 결정
-MR
이전 *백색잡음들의 선형결합으로 표현되는 모델
자기상관함수(ACF)를 활용 MA(q)모델 선정 '
잡음들의 선형 결함으로 미래를 결정.
선형 회귀는 종속, 독립.
여기는 백색잡음과 선형적으로
*백색 잡음: 시계열 모형의 오차항을 의미하며, 원인은 알려지지 않음/서로 독립이며 동일한 분포를 따름->회기모델에서 오차항이 존재. 시계열 데이터도 오차항을 가짐. -> 시계열 모델에서의 오차다. 오차들의 결합으로 표현되는 모델 -> MA
부분자기 상관함수
자기상관함수
ACF
오늘 1일전 2일전 3일전
오늘과 3일전이 얼마나 관계가 있는지 알아보는걸 상관계수 분석
=> 1일전과 2일전이 3일전 일에 영향을 끼친다.
PACF 1일전과 2일전은 배제하고 3일전만 고려
급격히 감소하는 이전 시점 선정 -> 다른 건 고려시점이 아니다.
PACF-> AR(3)모형
ACF->MA(3)모형
-ARIMA
AR 과 MA 가 결합된 모델
ARIMA(p,d,q)모델
p는 AR모형의 PACF로 도출
q는 MA모형의 ACF로 도출
d는 정상화를 위해 차분을 몇 번 했는지 의미
d=0이면 ARMA(p, q)모델
if p==0 : IMA
if q==0: ART
예측
회귀 예측
AR, MA, ARIMA, 딥러닝 -> 주가 예측, 기온 예측
회귀 모델 평가 지표
MSE, MAE, R-Square
분류 예측
딥러닝 -> 소음을 통한 제품 결합 확인, 자연어 처리(대화할 때 쓰는 말)
분류 예측 평가
혼동행렬, ROC Curve
