📍 피로도
💡 문제
XX게임에는 피로도 시스템(0 이상의 정수로 표현합니다)이 있으며, 일정 피로도를 사용해서 던전을 탐험할 수 있습니다. 이때, 각 던전마다 탐험을 시작하기 위해 필요한 "최소 필요 피로도"와 던전 탐험을 마쳤을 때 소모되는 "소모 피로도"가 있습니다. "최소 필요 피로도"는 해당 던전을 탐험하기 위해 가지고 있어야 하는 최소한의 피로도를 나타내며, "소모 피로도"는 던전을 탐험한 후 소모되는 피로도를 나타냅니다. 예를 들어 "최소 필요 피로도"가 80, "소모 피로도"가 20인 던전을 탐험하기 위해서는 유저의 현재 남은 피로도는 80 이상 이어야 하며, 던전을 탐험한 후에는 피로도 20이 소모됩니다.
이 게임에는 하루에 한 번씩 탐험할 수 있는 던전이 여러개 있는데, 한 유저가 오늘 이 던전들을 최대한 많이 탐험하려 합니다. 유저의 현재 피로도 k와 각 던전별 "최소 필요 피로도", "소모 피로도"가 담긴 2차원 배열 dungeons 가 매개변수로 주어질 때, 유저가 탐험할수 있는 최대 던전 수를 return 하도록 solution 함수를 완성해주세요.
⚠️ 제한사항
- k는 1 이상 5,000 이하인 자연수입니다.
- dungeons의 세로(행) 길이(즉, 던전의 개수)는 1 이상 8 이하입니다.
- dungeons의 가로(열) 길이는 2 입니다.
- dungeons의 각 행은 각 던전의 ["최소 필요 피로도", "소모 피로도"] 입니다.
- "최소 필요 피로도"는 항상 "소모 피로도"보다 크거나 같습니다.
- "최소 필요 피로도"와 "소모 피로도"는 1 이상 1,000 이하인 자연수입니다.
- 서로 다른 던전의 ["최소 필요 피로도", "소모 피로도"]가 서로 같을 수 있습니다.
✅ 풀이
👆 첫 번째 풀이 (성공)
사실 나는 풀이를 못했다. 문제 분류가 완전탐색이기 때문에 예전에 강의에서 들었던 것만 같은 DFS나 BFS를 사용해야 하나? 아니면 노가다로 모든 경우의 수를 탐색해야 하나? 하는 고민이 들었지만, 필요 피로도와 소모 피로도까지 생각하면서 어떻게 모든 경우를 탐색해야 하는지 떠오르지 않았다.
그래도 양심상 코틀린 풀이는 못 보겠고.. (뭘 보든 양심이 찔리긴 함) 재귀함수를 이용한 파이썬 풀이를 참고하였다. 함수의 동작 방식을 이미지로 그려보았다. 말로 설명하면 반복문 안에, 반복문 안에, 반복문 안에, ... 더이상 순회할 배열이 없을 때까지 반복하는 방식이다.
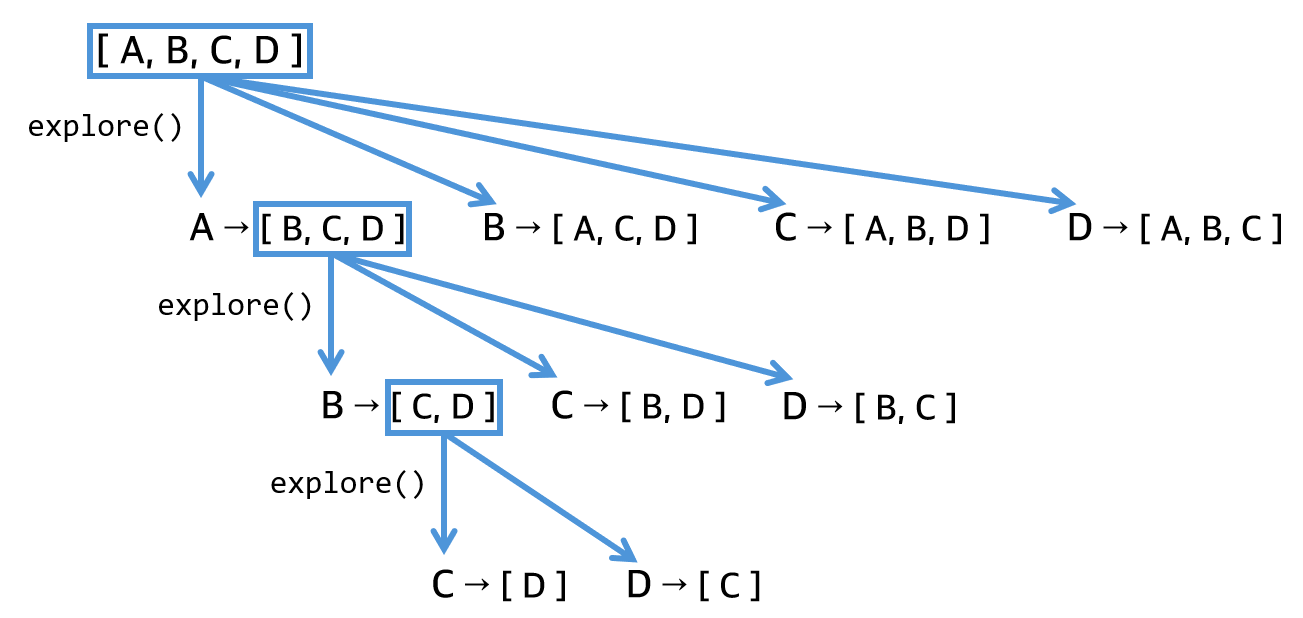
반복하는 방식은 이미지와 같고, 답을 구하기 위해서는 answer라는 Solution 클래스 멤버들이 모두 공유할 수 있는 변수를 만들어 현재 루프의 c(count)가 기존 answer(초기값 0이거나 다른 루프의 c였던 것)보다 크다면 바꾸는 방식을 사용했다.
class Solution {
var answer = 0
fun explore(p: Int, dg: List<IntArray>, c: Int = 0): Int {
var cnt = 0
for (d in dg) {
if (d[0] <= p) {
// 현재 던전을 제외한 나머지 던전들 목록
val left = dg.filter { it != d }
// 구한 나머지 던전들 목록으로 또 다시 모든 경우를 탐색 한다.
cnt = explore(p - d[1], left, c + 1)
// answer를 최대값으로 갱신
if (cnt > answer) answer = cnt
}
}
return if (answer > c) answer else c
}
fun solution(k: Int, dungeons: Array<IntArray>): Int {
explore(k, dungeons.toList())
return answer
}
}풀이 참고 없이는 절대.. 네버.. 풀지 못했다.
🔥 다른 사람의 풀이 1
사실 이 문제를 스스로 풀지 못하겠다고 생각한 순간부터 구글링을 엄청 했다. 그래프 탐색 알고리즘도 알아보고, 순열도 알아보고, (다른 사람 풀이도 찾아보고) ㅎ..
찾아본 풀이들은 커다란 틀은 비슷했지만, 위에서 내가 filter를 사용해 나머지 배열을 구한 것처럼 방문한 던전 외의 남은 던전을 구하는 방식에서 차이가 있었다.
이번 문제에서는 사실 던전의 최대 개수가 8개 밖에 되지 않아서 filter를 사용해도 시간 초과 같은 문제가 발생하지 않았지만, 만약 몇 백개의 던전이 주어졌다면 절대 통과할 수 없었을 것이다.
아무튼 돌아와서, 가장 많이 보인 풀이는 다음과 같다. 해당 던전을 방문했는지를 나타내는 배열을 따로 만들어 방문하지 않은 던전들을 탐색하는 방식이다. 이 때 주의할 점은 findAnswer 재귀 호출로 탐색을 다 마친 후에 꼭!! 방문 기록 초기화를 해줘야 한다. 그렇지 않으면 처음에는 [A, B, C, D]였던 애들인데 [B, C, D], [C, D], ... 이렇게 줄어든 상태로 탐색하게 된다.
class Solution {
private var answer = 0
fun solution(k: Int, dungeons: Array<IntArray>): Int {
// 방문 여부 저장 배열
val visited = BooleanArray(dungeons.size) { false }
findAnswer(k, dungeons, visited, 0)
return answer
}
fun findAnswer(k: Int, dungeons: Array<IntArray>, visited: BooleanArray, count: Int) {
for (i in dungeons.indices) {
if (visited[i] == false && k >= dungeons[i][0]) {
visited[i] = true
findAnswer(k - dungeons[i][1], dungeons, visited, count + 1)
visited[i] = false
}
}
if (count > answer) {
answer = count
}
}
}😶🌫️ 다른 사람의 풀이 2
가져온 또다른 풀이는 바로 solution 함수 자체를 재귀함수처럼 쓴 풀이이다. 게다가 이 분은 또 나머지 던전을 구할 때 sliceArray()를 사용했다. 문제에서 주어지는 입력인 k와 dungeons만 갖고 재귀를 구현할 수 있다는 것에 놀랐다.
풀이 방식은 정말 다 비슷하다. 주어진 던전들을 돌면서 모든 경우의 수를 탐색하고, 각 탐색마다 방문횟수를 구해 그 중 가장 큰 값을 반환하는 방식이다.
class Solution {
fun solution(k: Int, dungeons: Array<IntArray>): Int {
var maxN = 0
for (i in 0 until dungeons.count()) {
var d = dungeons[i]
if (k >= d[0]) {
var subN = solution(
k - d[1],
dungeons.sliceArray(0 .. i - 1) +
dungeons.sliceArray(i + 1 .. dungeons.count() - 1))
if (subN + 1 > maxN) maxN = subN + 1
if (maxN == dungeons.count()) return maxN
}
}
return maxN
}
}💭 후기
이쯤되면 슬슬 알고리즘도 알아가면서 해야겠다. 물론 알고리즘만 안다고 풀 수 있진 않겠지만, 도움은 되겠지.. 또 여러가지 문제도 풀어봐야겠다.

