연속된 부분 수열의 합 | 프로그래머스

김태영·2024년 7월 12일

코딩 테스트

목록 보기

30/33

📍 연속된 부분 수열의 합

💡 문제

비내림차순으로 정렬된 수열이 주어질 때, 다음 조건을 만족하는 부분 수열을 찾으려고 합니다.

기존 수열에서 임의의 두 인덱스의 원소와 그 사이의 원소를 모두 포함하는 부분 수열이어야 합니다.
부분 수열의 합은 k입니다.
합이 k인 부분 수열이 여러 개인 경우 길이가 짧은 수열을 찾습니다.
길이가 짧은 수열이 여러 개인 경우 앞쪽(시작 인덱스가 작은)에 나오는 수열을 찾습니다.

수열을 나타내는 정수 배열 sequence와 부분 수열의 합을 나타내는 정수 k가 매개변수로 주어질 때, 위 조건을 만족하는 부분 수열의 시작 인덱스와 마지막 인덱스를 배열에 담아 return 하는 solution 함수를 완성해주세요. 이때 수열의 인덱스는 0부터 시작합니다.

⚠️ 제한사항

5 ≤ sequence의 길이 ≤ 1,000,000
- 1 ≤ sequence의 원소 ≤ 1,000
- sequence는 비내림차순으로 정렬되어 있습니다.
5 ≤ k ≤ 1,000,000,000
- k는 항상 sequence의 부분 수열로 만들 수 있는 값입니다.

✅ 풀이

👆 첫 번째 풀이 (성공)

처음에 문제를 보고 최근에 탐색 알고리즘이 많이 나왔으니.. 너비 우선 탐색 알고리즘을 사용해야겠다 생각했다. 그런데 이 문제의 경우 "길이가 미정인 부분 배열"을 추출해 그 합이 k인지를 확인해야 되기 때문에 원소를 순서에 상관없이 하나씩 뽑아 탐색하는 너비 우선 탐색과는 거리가 멀었다. 멀어도 많이.. 멀었다.

아무튼, 문제를 풀이한 방식은 다음과 같다.

목표는 배열 가장 앞 쪽의, 가장 짧은 길이의, 총합이 k인 부분 배열이다.
- 범위를 구해야 하기 때문에 부분 배열의 시작과 끝을 저장할 변수 (start, end)를 선언해주었다.
- 총합이 동일한 배열 중 길이가 짧은 배열을 구해주기 위해 배열의 길이를 저장할 변수 l을 선언해주었다.
  - 초기값은 sequence.size + 1로, 만약 전체 배열이 답인 경우에도 갱신이 될 수 있게 해주었다.
배열 가장 앞 쪽의 부분 배열을 구해야되기 때문에 주어진 배열을 앞에서부터 탐색해나간다.
- 총합이 k를 넘어가는 경우 포함된 원소를 "앞에서부터" 제거해야 한다.
  - 이걸 위해 큐를 사용했다.
  - Java의 Queue를 사용할 수도 있지만, 오늘은 양방향으로 추가와 삭제가 가능한 Kotlin의 ArrayDeque를 사용했다.
  - 이유는 import 하기 싫어서...
- 총합이 k인 경우 위에서 선언한 변수 l과 길이를 비교해 더 짧다면 답을 갱신해준다.

class Solution {
    fun solution(sequence: IntArray, k: Int): IntArray {
        val dq = ArrayDeque<Int>()
        var sum = 0
        var l = sequence.size + 1
        var (start, end) = 0 to 0
        var answer = intArrayOf()
        
        sequence.mapIndexed { i, s ->
            dq.addLast(i)
            end = i
            sum += s
            
            // 합이 k를 넘어간다면,
            // k 이하가 될 때까지 큐 앞에서부터 제거
            while (sum > k) {
                sum -= sequence[dq.first()]
                dq.removeFirst()
                start++
            }
            
            // 합이 k인 부분 배열의 길이가 기존보다 더 짧다면 답 갱신
            if (sum == k && end - start < l) {
                answer = intArrayOf(start, end)
                l = end - start
            }
        }
        
        return answer
    }
}

🔥 다른 사람의 풀이

나는 그냥 큐를 이용해 풀었는데, 투 포인터와 이분 탐색으로 푸는 방법도 있다고 한다.

⭐ 투 포인터 알고리즘, Two Pointers
리스트에 순차적으로 접근해야 할 때 두 개의 점의 위치를 기록하면서 처리하는 알고리즘
시간복잡도 $O(N)$

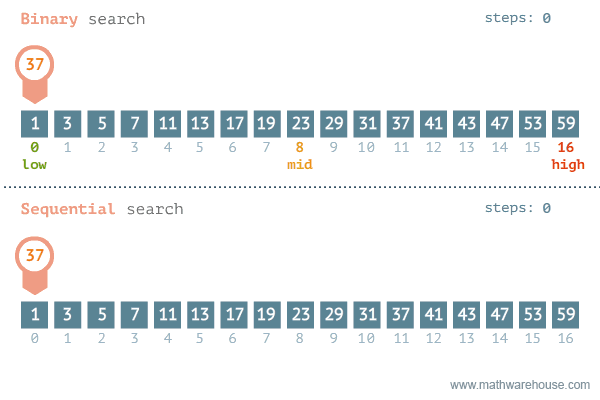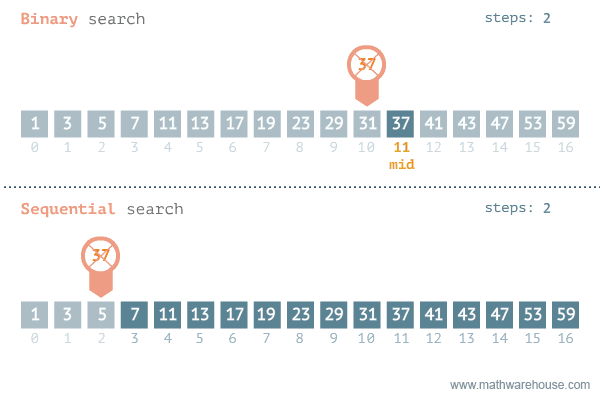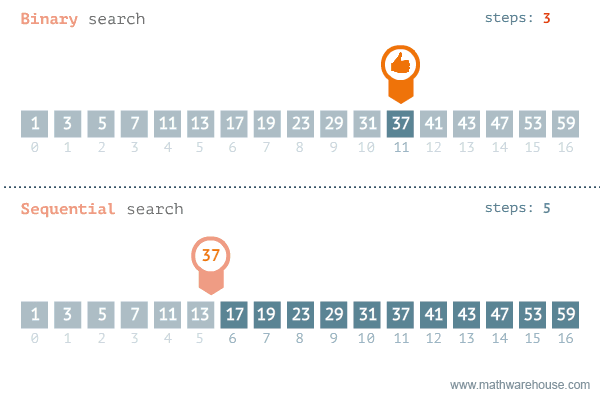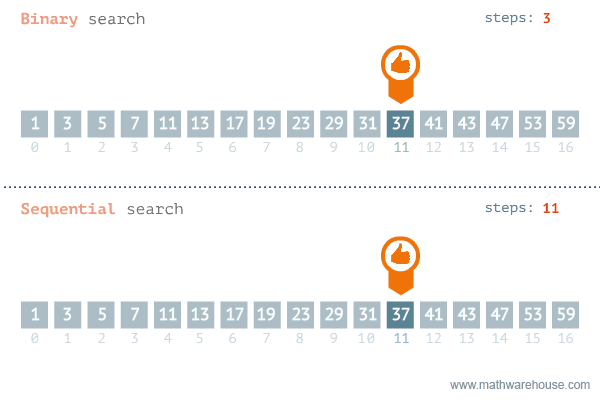
⭐ 이분 탐색(이진 탐색) 알고리즘, Binary Search
정렬된 배열에서 특정 값을 찾을 때 정중앙에 위치한 값을 활용해 탐색하는 알고리즘
원리 "중앙값 < 탐색값"이면 탐색값 보다 작은 부분(중앙값의 왼쪽)은 고려할 필요가 없다.
시간 복잡도 $O(\log{N})$

투 포인터

class Solution {
    fun solution(sequence: IntArray, k: Int): IntArray {
        var startPtr = 0
        var endPtr = 0
        var sum = sequence[0]

        val answer = intArrayOf(0, sequence.lastIndex)

        //투 포인터로 경우 탐색
        while(startPtr <= endPtr && endPtr < sequence.size){
            if(sum < k && ++endPtr < sequence.size)
                sum += sequence[endPtr]
            else if(sum > k)
                sum -= sequence[startPtr++]

            //길이가 짧다면(앞으로만 이동하므로 더 앞에 있을 가능성은 무시)
            if(sum == k){
                if(answer[1] - answer[0] > endPtr - startPtr) {
                    answer[0] = startPtr
                    answer[1] = endPtr
                }

                sum -= sequence[startPtr++]
            }
        }
        return answer
    }
}

이분 탐색

이 풀이를 보기 전에 도대체 합을 구하는 건데 어떻게 이분 탐색으로 푸는 건가 싶었다. 그런데 미리 합을 구해놓는 것이었고... 넘나 똑똑한것..

class Solution {
    fun solution(sequence: IntArray, k: Int): IntArray {
        var answer: IntArray = intArrayOf()
        
        // 누적합 미리 구해놓기
        val pSum = LongArray(sequence.size+1)
        for(i in 1 .. sequence.size) {
        	// 이전 인덱스까지의 합과 현재 인덱스의 값 더하기
            pSum[i] = pSum[i-1] + sequence[i-1]
        }
        
        // cnt로 k를 만드는 게 가능하다면 stop
        for(cnt in 1 .. sequence.size) {
            // cnt개로 k를 만드는 데 이분 탐색하여 가장 낮은 인덱스 탐색
            var left = -1
            var right = -1
            var s = 0
            var e = sequence.size-cnt
            while(s<=e){
                val mid = (s+e)/2
                
                // mid ~ mid+cnt까지의 합
                val sum = pSum[mid+cnt] - pSum[mid]
                if(sum >= k){
                    if(sum==k.toLong()){
                        left = mid
                        right = mid+cnt-1
                    }
                    e = mid-1
                }else{
                    s = mid+1
                }
            }
            if(left != -1 && right != -1) return intArrayOf(left,right)
        }
        return answer
    }
}