📙 노트북: Audio_Processing

오디오 처리(Audio Processing)

• 소리는 진동으로 인한 공기의 압축으로 생성
• 압축이 얼마나 됬느냐에 따라 진동하며, 공간이나 매질을 전파해 나가는 현상인 Wave(파동)으로 표현

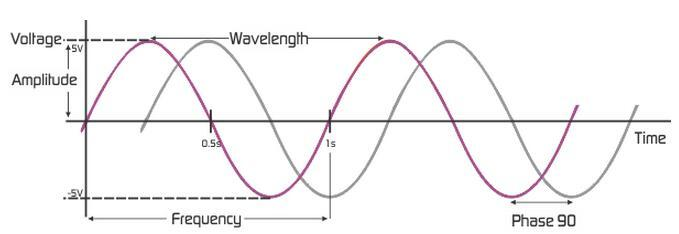
• 파동에서 얻을 수 있는 정보
  • 위상(Phase; Degress of displacement)
    
    • 동일 주파수에서 시간차/어긋남등을 표현하는 양
    • 시간 0시에 대한 파형의 상대적인 위치
  • 진폭(Amplitude; Intensity)
    • 신호의 세기(음성의 크기)
    • 신호의 높이
  • 주파수(Frequency)
    • 1초에 완성되는 주기의 횟수, 1초 동안 생성되는 신호 주기의 수
    • 초에 몇 번 주기가 반복되는지
    • 단위는 HZ(cycle/second)
  • 주기(Period, Wave length)
    • 한 사이클을 도는 데 걸리는 시간
    • 몇 초에 한번 반복이 되는가
    • T=1/f
    • 단위는 s
      
  • 대역폭(Bandwidth)
    • 신호에 포함된 최고 주파수와 최저 주파수의 차이

오디오 라이브러리

📙 노트북 참조

오디오 데이터

📙 노트북 참조

샘플링(Sampling)

Sampling

• 음성을 처리하기 위해 아날로그 정보를 잘게 쪼개 이산적인 디지털 정보로 표현해야 함
• 이때 무한히 쪼개서 저장할 수는 없으므로, 기준을 세워 아날로그 정보를 쪼개 대표값을 사용, 이를 샘플링이라 함
• 주로 사용할 때 시간을 기준으로 아날로그 정보를 쪼개는 Time Domain 방식을 사용
• Sampling rate
  • 1초당 추출되는 샘플 개수. 예를 들어, 44.1KHz는 1초를 44100 등분해서 오디오 데이터를 추출
  • sampling rate는 아날로그 정보를 얼마나 잘게 쪼갤지를 결정
  • 잘게 쪼갤수록 정보 손실이 줄어들지만, 데이터의 크기가 늘어남
• Sampling theorem
  • 디지털 변환을 하기위해 샘플링을 하게 돼 신호의 정보량이 손실됐지만 원래 신호로 복원하고 싶다. 어떻게 최대한 자연스럽게 원래의 신호로 복원할 수 있을까?
  • 나이퀴스트 정리(Nyquist Theorem): 원래 신호가 가진 최대 주파수의 2배 이상으로 샘플링하면 원래 신호를 충분히 재생할 수 있다는 정리
  • 40000Hz 이상의 sample rate로 샘플링을 실시하면 사람이 들을 수 있는 거의 모든 소리를 복원할 수 있다는 것
  • 일반적으로 sampling은 인간의 청각 영역에 맞게 형성(20~20000Hz)
    • Audio CD : 44.1 kHz(44100 sample/second)
    • Speech communication : 8 kHz(8000 sample/second) #유선전화

---

• 음성의 duration은 데이터의 길이와 sampling rate를 나누어 확인 가능

📙 노트북 참조

Resampling

• Resampling은 sampling data의 sampling rate를 조정해 다시 sampling하는 것
• 이때 일반적으로 보간(interpolation)을 할때는 low-pass filter를 사용
• librosa.resample을 사용하면 편리하게 resampling 가능
• 현재 데이터는 torch tensor, librosa는 numpy 배열을 받아들이기 때문에 변환 필요
• sampling rate를 절반으로 줄여, 길이도 절반으로 준 것을 확인할 수 있음
• sampling rate를 절반으로 줄이면, 음질도 저하됨(정보가 손실, 데이터 크기 감소)

📙 노트북 참조

Normalization & Quantization

• Normalization
  • 데이터간 음량이 제각각인 경우 normalization을 하여 amplitude를 [-1, 1] 범위로 조정
  • 여기서는 가장 간단한 방법인 데이터의 최대값으로 나눠주는 방법을 사용

📙 노트북 참조

• Quantization
  • 양자화란 실수 범위의 이산 신호를 정수(integer) 이산 신호로 바꾸는 것
  • 만약 8비트 양자화를 실시한다면 실수 범위의 이산 신호가 -128~127의 정수로 변환
  • 음질이 떨어지지만(noise가 심해짐) 용량은 줄어드는 형태
  • 양자화 비트 수(Quantization Bit Depth)가 커질 수록 원래 음성 신호의 정보 손실을 줄일 수 있지만 그만큼 저장 공간이 늘어나는 단점이 있다.

📙 노트북 참조

Mu-Law Encoding

• 사람의 귀는 작은소리의 차이는 잘잡아내는데 반해 소리가 커질수록 그 차이를 잘 느끼지 못함
• 사람은 100Hz에서 1000Hz에 이르는 구간의 소리는 주파수가 커질 수록 피치 역시 높아진다고 느끼는 경향
• 1000Hz 이상의 구간에서는 주파수와 피치 인식 사이의 관계가 로그 형태를 띈다(pitch correlates logarithmically with frequency)
• 1000Hz 이상의 구간에서는 주파수가 100배 정도 되어야 높낮이 차이를 2배라고 느끼는 정도
• 이러한 특성을 wave값을 표현하는데 반영해 작은 값에는 높은 분별력을, 큰 값끼리는 낮은 분별력을 갖도록 함

📙 노트북 참조

오디오 표현(Audio Representation)

• Sampling된 discrete한 데이터를 표현
  • 시간의 흐름에 따라, 공기의 파동의 크기로 보는 Time-Domain Representation 방법
  • 시간에 따라서 frequency의 변화를 보는 Time-Frequency Representation

Waveform - Time-Domain Representation

• Waveform은 오디오의 자연적인 표현
• 시간이 x축으로 그리고 amplitude가 y축으로 표현

정현파(Sinusoid) - Time-Frequency Representation

• 모든 신호는 주파수(frequency)와 크기(magnitude), 위상(phase)이 다른 정현파(sinusolida signal)의 조합으로 나타낼 수 있음
• 퓨리에 변환은 조합된 정현파의 합(하모니) 신호에서 그 신호를 구성하는 정현파들을 각각 분리해내는 방법

📙 노트북 참조

푸리에 변환(Fourier Transform)

• 푸리에 변환은 임의의 입력 신호를 다양한 주파수를 갖는 주기 함수들의 합으로 분해하여 표현하는 것을 의미

• 위의 그림은 두 개의 단순파(simple wave)가 시간 도메인에서 복합파(complex wave)로 표현

• 여기에 푸리에 변환을 실시하면 주파수 도메인에서 두 개의 주파수 성분으로 분해

• 주파수 도메인에 푸리에 변환을 실시하면 시간 도메인에서 복합파 생성 가능

• 푸리에 변환 식

  시각적으로 이해하는 푸리에 변환 : https://www.youtube.com/watch?v=Mc9PHZ3H36M

  • 퓨리에 변환의 식

    $y(t)=\sum_{k=-\infty}^\infty A_k \, \exp \left( i\cdot 2\pi\frac{k}{T} t \right)$

  • 진폭에 대한 수식

    $A_k = \frac{1}{T} \int_{-\frac{T}{2}}^\frac{T}{2} f(t) \, \exp \left( -i\cdot 2\pi \frac{k}{T} t \right) \, dt$

---

• 위 식에는 주기 함수들은 포함되어 있지 않음
• 오일러 공식에 따라 다음과 같이 지수 함수와 주기 함수간 관계를 나타낼 수 있음 $e^{i\theta} = \cos{\theta} + i\sin{\theta}$
  
• 해당 식을 오일러 공식에 따라 다음과 같이 표현 가능

$\exp \left( i\cdot 2\pi\frac{k}{T} t \right) = \cos\left({2\pi\frac{k}{T}}\right) + i\sin\left({2\pi\frac{k}{T}}\right)$

• 결국 푸리에 변환은 입력 신호에 상관없이 sin, cos 같은 주기 함수들의 합으로 분해 가능함을 나타냄

이산 푸리에 변환 (Discrete Fourier Transform, DFT)

• 우리가 샘플링한 데이터는 discrete data라고 할 수 있음
• 위의 푸리에 변환을 이산 영역으로 생각해볼 수 있음
• 특정 도메인(예컨대 시간)의 이산 신호(discrete signal)를 다른 도메인(예컨대 주파수)의 이산 신호로 변환하는 과정
• 우리가 수집한 데이터 $y_n$에서 이산 시계열 데이터가 주기 N으로 반복한다고 할때, DFT는 주파수와 진폭이 다른 N개의 사인 함수 합으로 표현 가능( 여러 주파수가 합쳐져 새로운 소리 표현)

$y_n = \frac{1}{N} \sum_{k=0}^{N-1} Y_k \cdot \exp \left( i\cdot 2\pi\frac{k}{N} n \right)$

• 위 식을 보면 k의 range가 0부터 $N-1$로 변화했음을 알 수 있음
• 이때 Spectrum $Y_{k}$는 원래의 시계열 데이터에 대한 퓨리에 변환값

$Y_k = \sum_{n=0}^{N-1} y_n\cdot \exp \left( -i\cdot 2\pi\frac{k}{N} n \right)$

• $y_{n}$ : input signal

• $n$ : Discrete time index

• $k$ : discrete frequency index

• $Y_{k}$ : k번째 frequeny에 대한 Spectrum의 값

• $y_n$은 식에서 보듯이 지수함수로 표현 할 수 있는데,
  이 지수 함수는 오일러 공식에서 봤듯이 주기함수의 합으로 표현 할 수 있고
  이 말은 여러가지 주기 함수의 합으로 어떤 시그널을 표현 할 수 있다는 의미

• spectogram을 보면 주파수랑 시간의 축으로 표현된다. ( wave-form은 amplitude만 시각화) 어떤 frequency영역대가 강한지를 시각화한게 spectogram, 이 값을 얻어내는게 FT

def DFT(x):
    N = len(x)
    X = np.array([])
    nv = np.arange(N)

    for k in range(N):
        s = np.exp(ij * 2 * np.pi * k / N * nv)
        X = np.append(X, sum(x * np.conjugate(s))) # frequency 영역을 append
    return x

Short-Time Fourier Transform(STFT)

• DFT는 시간에 흐름에 따라 신호의 주파수가 변했을때, 어느 시간대에 주파수가 변하는지 모름(소리를 한번에 처리하는 듯한 인상)
• STFT는 시간의 길이를 나눠서 퓨리에 변환
• 사람도 소리를 약 0.25초에 나눠 듣는다 → 컴퓨터도 시간에 따라 frequency의 값이 달라지는 것을 알고 싶다면? → STFT
• 주파수의 특성이 시간에 따라 달라지는 사운드를 분석하는 방법이며 우리가 사용하는 signal 데이터에 적합
• 시계열 데이터를 일정한 시간 구간 (window size)로 나누고, 각 구간에 대해서 스펙트럼을 구함
• 우리가 보통 딥러닝에서 사용하는 input data가 이 정보
• STFT에 대한 식과 설명은 다음과 같음

$X(l,k) = \sum_{n=0}^{N-1} w(n) x(n+lH)\exp^{\frac{-2\pi k n}{N}}$

• $N$ : FFT size
  • Window를 얼마나 많은 주파수 밴드로 나누는가
• Duration
  • 샘플링 레이트로 window를 나눈 값
  • $T= window/SR$
  • T(Window) = 5T(Signal), duration은 신호주기보다 5배 이상 길게 잡아야함
  • 440Hz 신호의 window size는 5*(1/440)
• $w(n)$ : Window function 일반적으로 Hann window 사용
  
• $n$ : Window size
  • Window 함수에 들어가는 Sample의 양
  • 작을수록 Low-frequency resolution을 가지게 되고, high-time resolution을 가짐
  • 길수록 High-frequency, low time resolution을 가짐
  • FFT size와 같으면 좋다고 한다
• $H$ : Hop size
  • 윈도우가 겹치는 사이즈, 일반적으로는 1/4정도를 겹치게 함(끊김 없이 처리하기 위해)
  • 음성신호처리에서 frame 생성시 overlap을 하는 이유
  • overlapping window는 frame의 양 끝단에서 신호의 정보가 자연스럽게 연결되게 하기 위해 사용한다
• STFT의 결과는 즉 시간의 흐름(Window)에 따른 Frequency영역별 Amplitude를 반환

📙 노트북 참조

윈도우 함수

• Windowing이란 각각의 프레임에 특정 함수를 적용해 경계를 스무딩하는 기법
• Window function 기능

  1. main-lobe의 width를 제어

  2. side-lobe의 레벨 trade-off를 제어

  3. 깁스 현상(불연속을 포함하는 파형이 푸리에 합성되었을 때 불연속 값에서 나타나는 불일치 현상) 방지

     window function을 쓰는 이유

• 플롯을 보게 된다면 windowing을 적용하기전 plot은 끝부분이 다 다르지만, windowing을 지나고 나서 나오는 plot은 끝이 0 으로 일치한다는 특성을 볼 수 있습니다.

윈도우 크기

• window size는 time과 frequency의 resolutions를 제어
  • short-window - 낮은 frequency resolutuon, 높은 time resolution
  • long-window - 높은 frequency resolution, 낮은 time resolution
  • Heisenberg's Uncertainty principle of Fourier Transform Time resolution과 Frequency resolution에는 trade off가 존재 window size를 키우고 그 size 만큼의 point로 FFT를 하면 더 높은 resolution을 가진 frequency를 구할 수 있다. 즉 1 Hz와 2Hz를 구분할 수 있게 되는 것이다. 그러나 이렇게 하게 되면 그 길어진 window 중에서 정확히 어느 시점에서 그 frequency event가 발생했는지는 더 불명확해 진다. 반대로 정확히 언제인지를 알아내고자 window를 줄이면, 더 낮은 resolution의 frequency를 얻게 된다.
    

time window 길이와 주파수 해상도

스펙트로그램

• 스펙트로그램은 소리나 파동을 시각화하여 파악하기 위한 도구
• 파형과 스펙트럼의 특징이 조합되어 있음
• 시간 축과 주파수 축의 변화에 따라 진폭의 차이를 인쇄 농도나 표시 색상 차이로 표현

Linear Frequency Scale

• 순음(single tone)들의 배음 구조를 파악하는데 적절
• 분포가 저주파수 영역에 치우쳐져 있음

맬 스케일

• 주파수 단위를 다음 공식에 따라 멜 스케일로 변환 (cf.Mu-law는 Amplitude 단위에 대한 전처리) $m = 2595 \log_{10}\left(1 + \frac{f}{700}\right)$
  
• 일반적으로 mel-scaled bin을 FFT size보다 조금 더 작게 만듬
• mel-scaled bin 사이즈를 줄이면 정보가 압축되며, 압축된 만큼 노이즈가 적음(데이터가 바뀌지는 않고, 중요한 정보가 압축)

📙 노트북 참조

• mel-scaled bin 사이즈 잡는 팁? 데이터 class 별로 spectogram을 추출하여 평균 값을 보면 어떤 Frequency 영역대를 잡으면 좋을 지 분별력이 생기고 그에 따라 사이즈를 정할 수 있다. 물론 실험하는 게 더 빠르긴 하다..
  
• 해당 scale을 적용해 spectogram을 만든 것이 melspectogram

바크 스케일

• 귀가 인식하는 주파수의 영역은 대략 20Hz∼20000Hz로 가정, 하지만 주파수에 대한 사람의 인식은 비선형적
• 귀와 뇌의 가청대역을 24개의 대역으로 나눈것을 Bark라고 함
• Bark scale은 500Hz 이하에서는 100Hz의 대역폭을, 500Hz 이상에서는 각 대역의 중심주파수의 대략 20%에 해당하는 대역폭을 가짐 20, 100, 200, 300, 400, 510, 630, 770, 920, 1080, 1270, 1480, 1720, 2000, 2320, 2700, 3150, 3700, 4400, 5300, 6400, 7700, 9500, 12000, 15500 ( Hz )
  

Log Compression

• 신호를  $10 * log10(\frac{S}{ref})$의 단위로 신호를 스케일링
• spectrogram을 데시벨 유닛으로 전환
  

    log_mel_S = librosa.power_to_db(mel_S)
    print(log_mel_S.shape)

이산 코사인 변환(Discrete Cosine Transform, DCT)

• DCT는 n개의 데이터를 n개의 코사인 함수의 합으로 표현하여 데이터의 양을 줄이는 방식
• 저 주파수에 에너지가 집중되고 고 주파수 영역에 에너지가 감소

오디오 특징 추출(Audio Feature Extraction)

• 모든 오디오 신호는 많은 기능으로 구성
• 해결하려는 문제와 관련된 특성 추출 필요

스펙트럼 센트로이드(Spectral Centroid)

• 주파수의 스펙트럼의 가중 평균과 같음

스펙트럼 롤오프(Spectral Rolloff)

• 신호의 모양을 측정
• 고주파수가 0으로 감소하는 주파수를 나타냄

스펙트럼 대역폭(Bandwidth)

• 스펙트럼 대역폭은 최대 피크의 절반 (또는 최대 절반의 전체 너비 [FWHM])에서 빛의 대역 폭으로 정의되며 두 개의 수직 빨간색 선과 파장 축에서 λSB로 표시

spectral_bandwidth_2 = librosa.feature.spectral_bandwidth(audio_np+0.01, sr=sr)[0]
spectral_bandwidth_3 = librosa.feature.spectral_bandwidth(audio_np+0.01, sr=sr, p=3)[0]
spectral_bandwidth_4 = librosa.feature.spectral_bandwidth(audio_np+0.01, sr=sr, p=4)[0]

plt.figure(figsize=(14, 6))
librosa.display.waveplot(audio_np, sr=sr, alpha=0.4)
plt.plot(t, minmax_scale(spectral_bandwidth_2, axis=0), color='y', alpha=0.5)
plt.plot(t, minmax_scale(spectral_bandwidth_3, axis=0), color='g', alpha=0.5)
plt.plot(t, minmax_scale(spectral_bandwidth_4, axis=0), color='r', alpha=0.5)
plt.legend(('p=2', 'p=3', 'p=4'))

제로 크로싱 비율(Zero Crossing Rate)

• 신호의 부드러움을 측정하는 매우 간단한 방법은 해당 신호의 세그먼트 내에서 제로 크로싱 수를 계산하는 것
• 음성 신호는 느리게 진동 (예를 들어, 100Hz 신호는 초당 제로 100을 교차하는 반면 무성 마찰음은 초당 3000 개의 제로 교차를 가질 수 있음)

• zoom (8000~8100)

zero_crossings = librosa.zero_crossings(audio_np[n0:n1], pad=False) # zoom 영역을 slicing
print(zero_crossings.shape)
print(sum(zero_crossings)) # Count the number of zero_crossings , 47

zcrs = librosa.feature.zero_crossing_rate(audio_np)
print(zcrs.shape)

Mel-Frequency Cepstral Coefficients (MFCC)

• 신호의 MFCC(Mel frequency cepstral coefficients)는 스펙트럼 포락선의 전체 모양을 간결하게 설명하는 작은 기능 집합 (일반적으로 약 10-20)
• 인간 목소리의 특성을 모델링

• 음성 인식과 관련해 불필요한 정보는 버리고 중요한 특질만 남긴 피처(feature)

• 음성학, 음운론 전문가들이 도메인 지식을 활용해 공식화한 것

• 입력 음성을 짧은 구간(대개 25ms 내외)으로 나눕니다. 이렇게 잘게 쪼개진 음성을 프레임(frame)

• 프레임 각각에 푸리에 변환(Fourier Transform)을 실시해 해당 구간 음성(frame)에 담긴 주파수(frequency) 정보를 추출 → 스펙트럼(spectrum)

• 스펙트럼에 사람의 말소리 인식에 민감한 주파수 영역대는 세밀하게 보고 나머지 영역대는 상대적으로 덜 촘촘히 분석하는 필터(Mel Filter Bank)를 적용 → 멜 스펙트럼(Mel Spectrum)

• 멜 스펙트럼에 로그를 취하면 → 로그 멜 스펙트럼(log-Mel Spectrum)

• 멜 스펙트럼 혹은 로그 멜 스펙트럼은 태생적으로 피처(feature) 내 변수 간 상관관계(correlation)가 존재

• 멜 스케일 필터는 헤르츠 기준 특정 주파수 영역대의 에너지 정보가 멜 스펙트럼 혹은 로그 멜 스펙트럼의 여러 차원에 영향을 주는 구조입니다.
  

• 로그 멜 스펙트럼에 역푸리에 변환(Inverse Fourier Transform)을 수행해 변수 간 상관관계를 해소한 피처를 Mel-frequency Cepstral Coefficients(MFCCs)

MFCC에 대한 더 자세한 설명

크로마그램(Chromagram)

• 색도 특성 또는 벡터는 일반적으로 각각의 피치 클래스의 많은 에너지가, {C, C #, D, D 번호는, E, ..., B} 신호 내에 존재하는 방법을 나타내는 요소 특징 벡터
• 음악 작품 간의 유사성 측정을 설명하는 강력한 방법 제공

📙 노트북 참조

오디오 필터(Audio Filter)

• low-pass filter
  • 낮은 주파수를 내보내는 필터, 고 음역대 주파수 배음을 깎아나가면서 차단(cut off) 주파수를 기준으로 낮은 주파수만 통과 시켜 저 음역대를 살려 놓기 때문에 꽉 찬 소리를 만들어 냅니다.

📙 노트북 참조

참고

• https://www.youtube.com/watch?v=FjYNM3YGFB4
• https://newsight.tistory.com/294
• https://socratic.org/questions/how-do-you-calculate-the-period-and-frequency
• https://yeji1214.tistory.com/43
• https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=gkenq&logNo=220679236344&view=img_7