문제: 편의를 위해 고속도로는 평면상의 직선이라고 가정하고, 센서들은 이 직선 위의 한 기점인 원점으로부터의 정수 거리의 위치에 놓여 있다고 하자. 따라서, 각 센서의 좌표는 정수 하나로 표현된다. 이 상황에서 각 집중국의 수신 가능영역의 거리의 합의 최솟값을 구하는 프로그램을 작성하시오. 단, 집중국의 수신 가능영역의 길이는 0 이상이며 모든 센서의 좌표가 다를 필요는 없다.
예제 2를 예로 들어보면
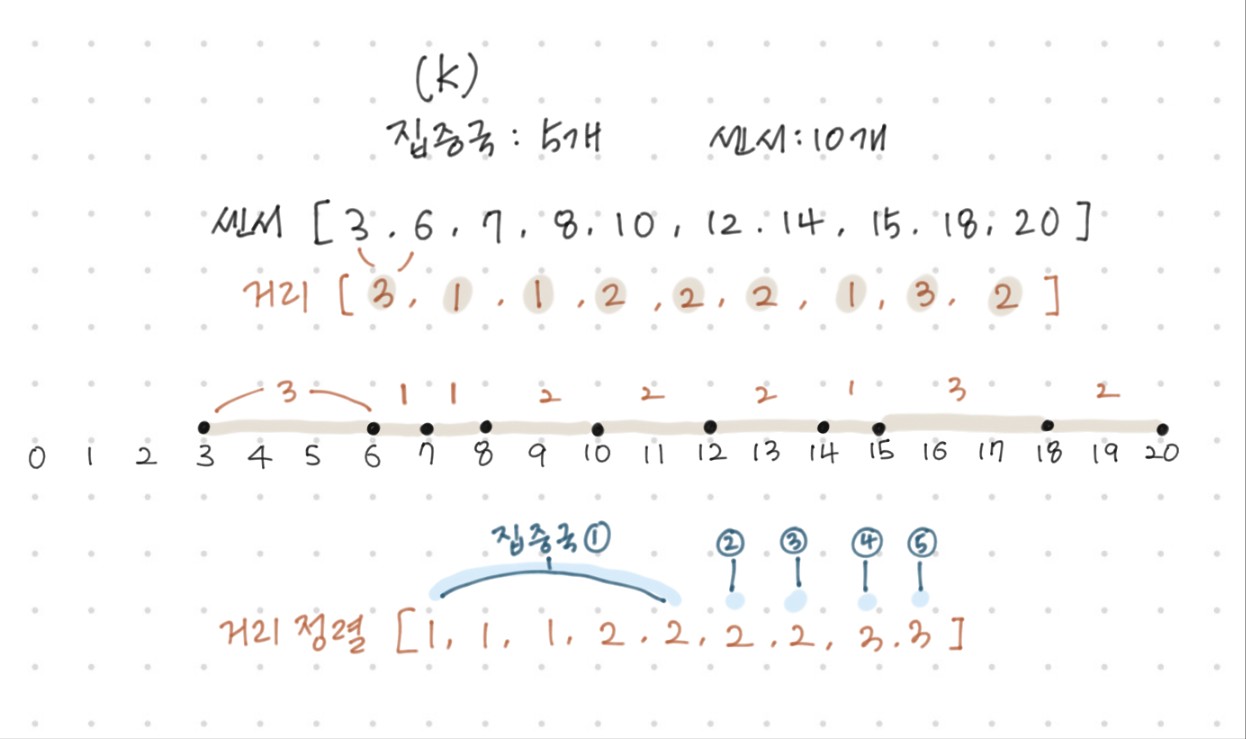
집중국이 커버 가능한 최소의 길이를 구해야 하니까 센서들을 정렬시켜서 센서 간 사이의 거리를 구한다.
센서:
[20, 3, 14, 6, 7, 8, 18, 10, 12, 15]
정렬된 센서:
[3, 6, 7, 8, 10, 12, 14, 15, 18, 20]
센서 간 거리:
[3, 1, 1, 2, 2, 2, 1, 3, 2]
정렬된 센서간 거리:
[1, 1, 1, 2, 2, 2, 2, 3, 3]
이렇게 센서들이 정렬된 상태에서, 집중국이 커버해야 할 최소의 거리를 구하는 방법은 센서 간 거리 리스트에서 큰 순서대로 (집중국 개수(k) - 1)개를 제거하는 방법이다.
처음엔 이 부분이 이해가 안 가서 찾아보았고 조금 더 작은 단위의 예시를 통해 이해할 수 있었다.
예를 들어, 센서 간 정렬된 거리 리스트가 [1, 2, 2, 2, 3] 라고 했을 때, 집중국 개수(k)가 2라면, 센서들을 두 개의 그룹으로 나누어야 한다.
즉, 여기서 거리 3을 제거하여 연결을 끊고 나머지 거리의 차들을 다 더하면 이것이 최소값이 된다.
이를 식으로 나타내면 k-1개를 전체 리스트에서 제거한 다음, 나머지 거리들의 합을 구하면 된다.
다시 우리의 예제로 돌아와보면,
집중국 개수(k)가 5이기 때문에 다섯개의 그룹으로 나눈다고 생각할 수 있다. 즉, 여기서 가장 큰 거리 k-1개를 전체 리스트에서 제거한 다음, 나머지 거리들을 합하면 1+1+1+2+2=7이 각 집중국의 수신 가능영역의 거리의 합의 최솟값이 된다.
위의 그림을 통해 집중국이 담당하는 영역을 확인할 수 있다.
이를 코드로 나타내면 아래와 같다.
from sys import stdin
input = stdin.readline
n = int(input())
k = int(input())
dot = list(map(int, input().split()))
dot.sort() # [3, 6, 7, 8, 10, 12, 14, 15, 18, 20]
a = [] # 센서 간의 거리
for i in range(1, n):
a.append(dot[i] - dot[i - 1]) # [3, 1, 1, 2, 2, 2, 1, 3, 2]
a.sort() # [1, 1, 1, 2, 2, 2, 2, 3, 3]
for _ in range(k - 1): # k = 5 -> 4
if not a: # 가장 큰 값 4개 제거
break
a.pop() # [1, 1, 1, 2, 2]
print(sum(a)) # sum[1, 1, 1, 2, 2]같은 내용이지만 좀 더 간단한 코드이다.
from sys import stdin
input = stdin.readline
n = int(input())
k = int(input())
s = list(map(int, input().split()))
s.sort()
dis = [s[i] - s[i-1] for i in range(1, n)]
dis.sort(reverse=True)
print(sum(dis[k-1:]))