내리막 길 C++ - 백준 1520

https://www.acmicpc.net/problem/1520

이 문제는 dfs와 dp를 잘 조합해 활용해야 풀 수 있는 문제이다.

dfs만 사용하게 되면 최악의 경우 약 4^(500*500)의 시간 복잡도가
생길 수 있다.

따라서 dp를 적절히 활용해야하는데, 그 방법 중에 하나가
아래와 같다.

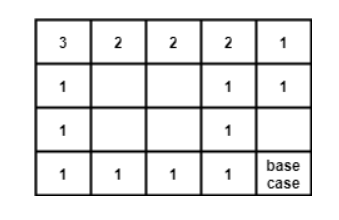
0,0에서 n-1,m-1로 갈 때 한 점에서의 가는 방법은 다음 점의 방법 + 점에 오는 경우의 수이다.

따라서 점화식은 다음과 같이 작성할 수 있다.

dp[현재 점]+=dp[다음 점]

dp[다음점] 부분은 dfs로 돌려주고 n-1,m-1에 도달했을 시 1가지 방법이
있으므로 1을 리턴해준다.

그런데 어떤 점에 2번 이상 방문하게 되면 위 점화식이 2번이상 수행되므로
그 점을 주의하여 코드를 작성한다.

코드는 다음과 같다.

#include <bits/stdc++.h>
#define FASTIO ios_base :: sync_with_stdio(false); cin.tie(NULL);
#define MAX 500+1
using namespace std;

int n,m;
int graph[MAX][MAX];
int dp[MAX][MAX];

int dx[4]={1,-1,0,0};
int dy[4]={0,0,1,-1};

int dfs(int x, int y){
	if(x==n-1 && y==m-1) return 1;
	if(dp[x][y]!=-1) return dp[x][y];
	
	dp[x][y]=0;
	
	for(int i=0;i<4;i++){
		int nx=x+dx[i];
		int ny=y+dy[i];
		
		if(0<=nx && nx<n && 0<=ny && ny<m){
			if(graph[nx][ny]<graph[x][y]){
				dp[x][y]+=dfs(nx,ny);
			}
		}
	}
	return dp[x][y];
}

int main(){
	FASTIO
	memset(dp,-1,sizeof(dp));
	cin >> n >> m;
	for(int i=0;i<n;i++){
		for(int j=0;j<m;j++){
			cin >> graph[i][j];
		}
	}
	dfs(0,0);
	cout << dp[0][0];
}

이미지 출처 : https://hackids.tistory.com/109