https://www.acmicpc.net/problem/2166

문제에 사용되는 알고리즘
1.벡터의 외적
벡터의 외적이란 벡터 곱 중 하나로써, 내적과는 다르게 스칼라 값이 아닌
외적이 진행된 후에는 벡터값이 도출된다.
두 3차원 벡터 와 에 대해
외적을 시행하면 다음과 같이 표현될 수 있다.

하지만 우리가 다룰 것은 2차원 벡터의 외적이기에 와 는 0으로 둘 것이다.
따라서 결과는 로 표현된다.
두 벡터에 대한 외적 값은 두 벡터의 수직인 벡터인데, 외적의 시작을 어떤 벡터부터 하느냐에 따라 벡터의 부호가 바뀐다.
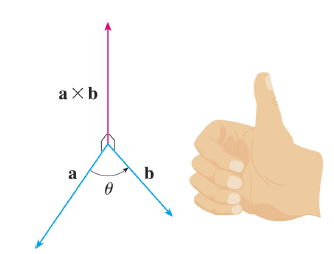
위 사진처럼 는 외적 값이 양수, 인 경우는 크기는 같고
부호가 다른 벡터가 도출된다.
벡터의 외적은 다음과 같이 정의된다.

따라서 두 벡터가 이루는 모양이 어떤 모양인지 알 수 있다.
예를 들어 점 가 있을 때
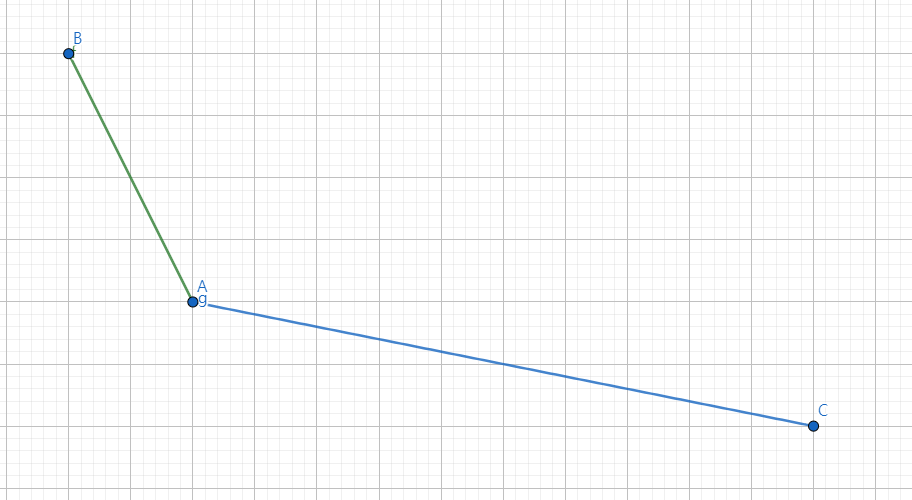
벡터 와 를 외적하면 가 나온다.
양수 9가 나왔다.
CCW(CounterClockWise) 알고리즘이란?
CCW 알고리즘은 한국어로 직역하면 반시계방향 알고리즘인데,
세 점의 좌표가 주어지면 그 좌표들이 어떤 방향으로 배치되어 있는지
구분할 수 있게 해주는 알고리즘이다.
CCW는 벡터의 외적을 이용해 구하는데,
위 예제에서 와 를 외적했을때
x,y축에 수직인 벡터 가 나왔다.
이 벡터의 z축 값이 양수이면 세 점 A,B,C를 차례대로 보았을 때
시계방향으로 이루어져있는 것을 나타내고,
음수라면 반시계, 0이라면 수직선 위에 세 점이 있다는 사실을 나타낸다.
문제 접근
그렇다면 넓이는 어떻게 구할 것인가?
일반적으로 각형에 대해 0번째 점을 포함한 삼각형으로 나누어서 더해주면 된다.

세 점이 주어졌을 때 위 공식으로 삼각형의 넓이를 구할 수 있게 된다.
삼각형의 두 변 길이를 라고 하고 이루는 각의 크기를 라고 할 때,
이므로,
외적을 한 후 2로 나누어주면 된다.
오목다각형의 처리
사실 필자는 CCW를 모르는 상태로 세 변의 길이와 코사인 법칙을 활용하여
사인값을 구하고 푸는 방식으로 접근했는데 오목다각형을 고려하지 않아 틀렸다.
그러면 오목다각형은 어떻게 고려해주어야 할까?
오목 다각형의 경우 CCW의 리턴값은 반시계 방향이므로 양수이고,
볼록 다각형의 경우 시계방향으로 음수이다.
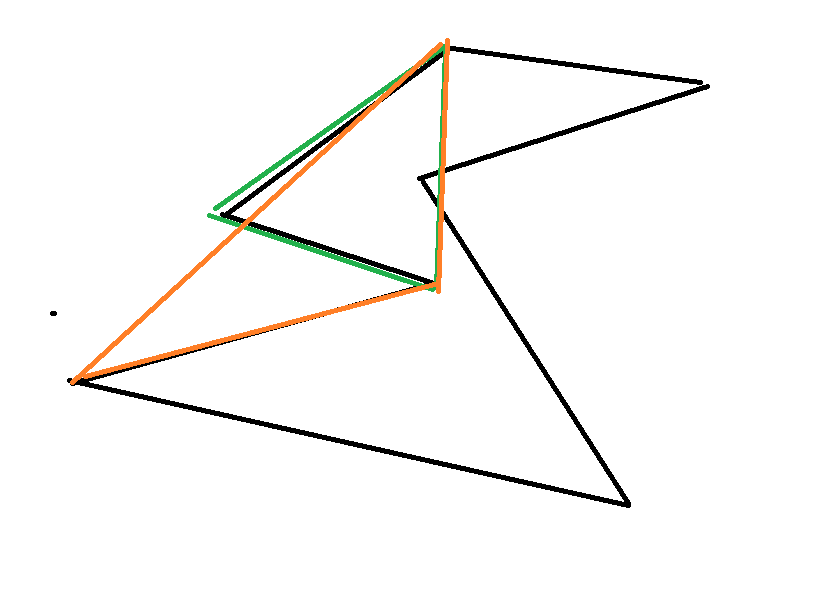
다음과 같은 다각형일 때 볼록삼각형인 초록색 삼각형은 제대로 된 넓이를 구해줄 수 있지만,
주황색 삼각형의 경우 잘못된 넓이를 구하게 된다.
하지만 CCW의 값은 부호가 반대가 되므로 진짜 넓이는 음수로,
빼야하는 넓이는 양수로 표현되어 정확한 답이 도출된다.
(3개씩 ccw를 돌리지 않는 이유는 n개를 한꺼번에 외적했을 때와 값이 동일하기 때문이다.)
이를 토대로 구현한 코드는 다음과 같다.
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
int n;
double ans=0;
int main(){
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
cin >> n;
vector<pair<ll, ll>> arr(n+1);
for(int i=0;i<n;i++) cin >> arr[i].first >> arr[i].second; arr[n]=arr[0];
for(int i=0;i<n;i++) ans+=arr[i].first*arr[i+1].second;
for(int i=0;i<n;i++) ans-=arr[i].second*arr[i+1].first;
ans=round(ans*5)/10;
cout.precision(1);
cout << fixed;
cout << abs(ans);
return 0;
}