미로탐색 C++ - 백준 2178

https://www.acmicpc.net/problem/2178

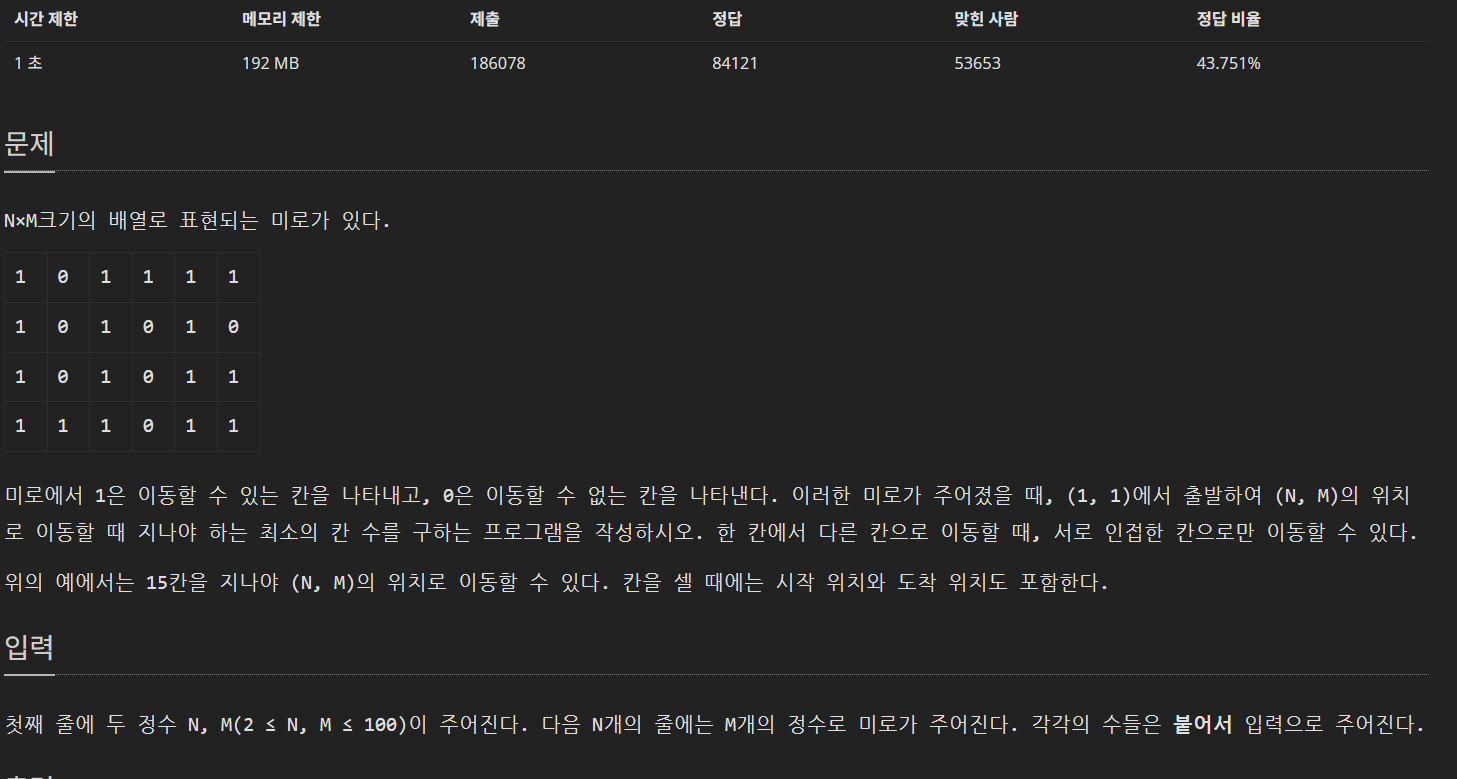
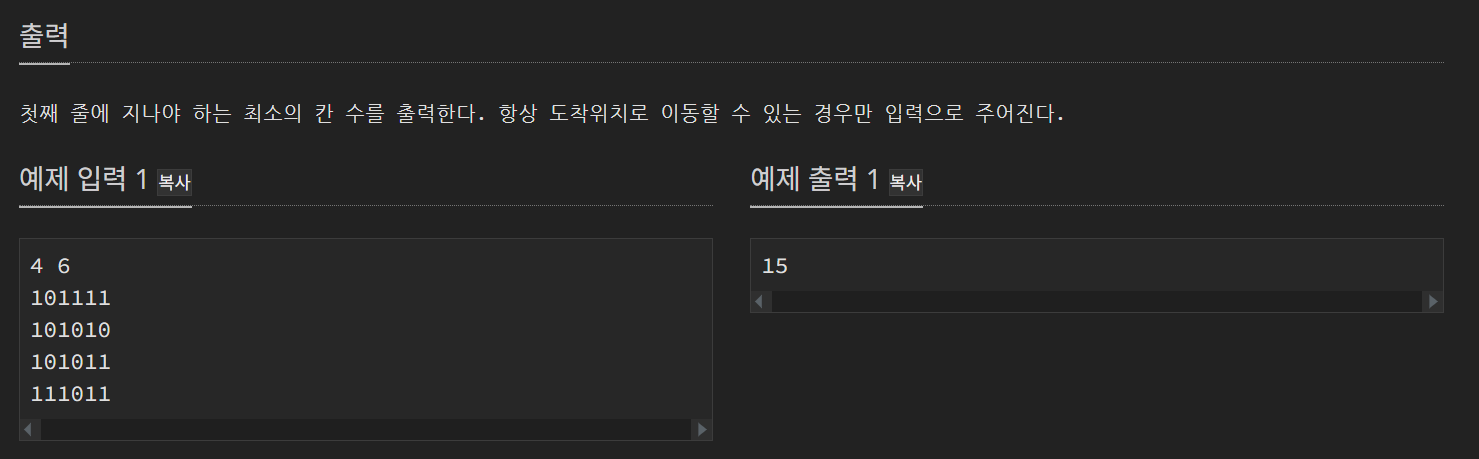
이 문제는 최단 경로의 문제이기 때문에
최단 경로 문제에 유리한 bfs를 사용해 풀어야 한다.

먼저 bfs는 dfs와 달리 큐에 있는 노드들(몇 개 정도)의 탐색 범위의 깊이가 유사하다.

따라서 같은 깊이에 있는 노드들을 동시에 탐색하기 좋은데, 이를 활용하여 미로 탐색에 적용해 문제를 풀었다.

먼저 코드는 다음과 같다.

#include <bits/stdc++.h>
using namespace std;

int N;
int M;
int graph[10001][101];
bool visited[10001][101];
int dx[4]={1,-1,0,0};
int dy[4]={0,0,1,-1};

void dfs(){
	queue<pair<int, int>> q;
	q.push(make_pair(0,0));
	visited[0][0]=true;
	graph[0][0]=1;
	while(!q.empty()){
		int x=q.front().first;
		int y=q.front().second;
		q.pop();
		for(int i=0;i<4;i++){
			int nx=x+dx[i];
			int ny=y+dy[i];
			
			if(0<=nx && nx<N && 0<=ny && ny<M){
				if(!visited[nx][ny] && graph[nx][ny]!=0){
					graph[nx][ny]=graph[x][y]+1;
					visited[nx][ny]=true;
					q.push(make_pair(nx,ny));
				}
			}
		}
	}
}

int main(){
	cin >> N >> M;
	for(int i=0;i<N;i++){
		for(int j=0;j<M;j++){
			scanf("%1d", &graph[i][j]);
		}
	}
	dfs();
	cout << graph[N-1][M-1];
}

bfs 탐색 시 0으로 되어 있는 부분(벽), 이미 탐색했으면 다시 탐색하지 않았고, 범위를 벗어나는 부분도 if문으로 처리했다.

또한 graph[nx][ny]에는 graph[x][y], 탐색되도록 하는 노드의 최단 경로에 +1을 하므로써 graph[N-1][M-1]에는 최단 경로의
타일 수만 남게 된다.