색종이 만들기 C++ - 백준 2630

https://www.acmicpc.net/problem/2630

분할 정복이란 큰 문제를 여러가지 문제로 쪼개어

해결할 수 있는 작은 문제들을 해결해 큰 문제의 답을

구하는 문제 풀이 방법론이다.

분할 정복을 사용한 예는 대표적으로 병합 정렬(merge sort)가 있다.

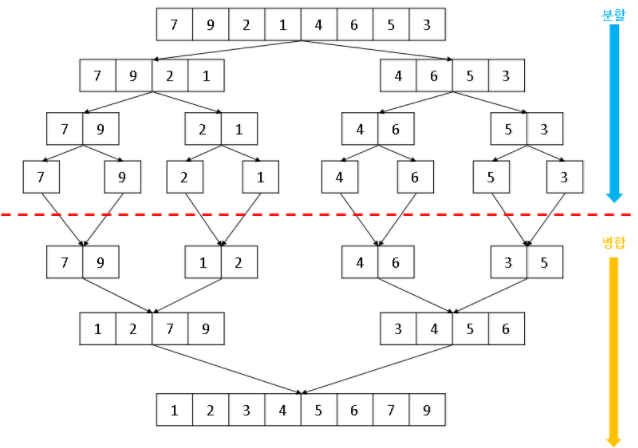
병합 정렬은 분할 정복을 사용하여 진행된다.

배열의 원소가 1개가 될 때까지 분할하고 $O(logN)$

원소가 1개인 배열 사이 비교를 통해 배열을 합치고,

2개인 배열을 합치고...

(재귀적인 과정을 거쳐...)

총 n번의 비교과정이 있다.

(따라서 시간 복잡도는 $O(NlogN)$이 된다.)

문제 접근

색종이의 최대 길이가 $2^7$이므로

최악의 경우 $2^{7\cdot 2}\cdot log_4{2^{28}}$ -> $14\cdot 2^{14}$번 연산하기 때문에

완전 탐색을 해도 제한 시간을 통과한다.

풀이 과정

문제의 요구대로 색종이에 다른 색이 껴있으면 나누고,

다른 색이 없다면 색종이 개수를 늘려주면 된다.

코드는 다음과 같다.

#include <bits/stdc++.h>
using namespace std;

int n;
int ans[2]={0,};
bool f[128][128];

void solve(int x, int y, int c){
    bool stc=f[x][y];
    if(c==1){ans[stc]++;return;}
    bool b=false;
    for(int i=0;i<c;i++){
        for(int j=0;j<c;j++){
            if(f[x+i][y+j]!=stc){b=true;break;}
        }
        if(b) break;
    }
    if(!b) ans[stc]++;
    else{
        solve(x,y,c/2);
        solve(x,y+c/2,c/2);
        solve(x+c/2,y,c/2);
        solve(x+c/2,y+c/2,c/2);
    }
}

int main(){
    ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
    cin >> n; for(int i=0;i<n;i++) for(int j=0;j<n;j++) cin >> f[i][j];
    solve(0,0,n);
    cout << ans[0] << '\n' << ans[1];
    return 0;
}

이미지 출처