체스판 다시 칠하기 2 C++ - 백준 25682

https://www.acmicpc.net/problem/25682

이 문제는 체스판 다시 칠하기 1과는 다르게 $N,M$의 범위의

상한이 $2000$이기 때문에 매번 $K\cdot K$의 경우를 확인하면 TLE가 난다.

따라서 다른 방법을 써야 하는데, 매번 확인하는 비용이 $O(1)$인

누적합을 사용하여 이 문제를 풀 수 있다.

시간복잡도는 $O(N^2)$으로 볼 수 있다.

문제 접근

이 문제의 누적합은 상당히 인상적이었다.

누적합을 구할 때 식을 세우는 과정이 $DP$와 비슷했기 때문이다.

아래 사진을 보자.

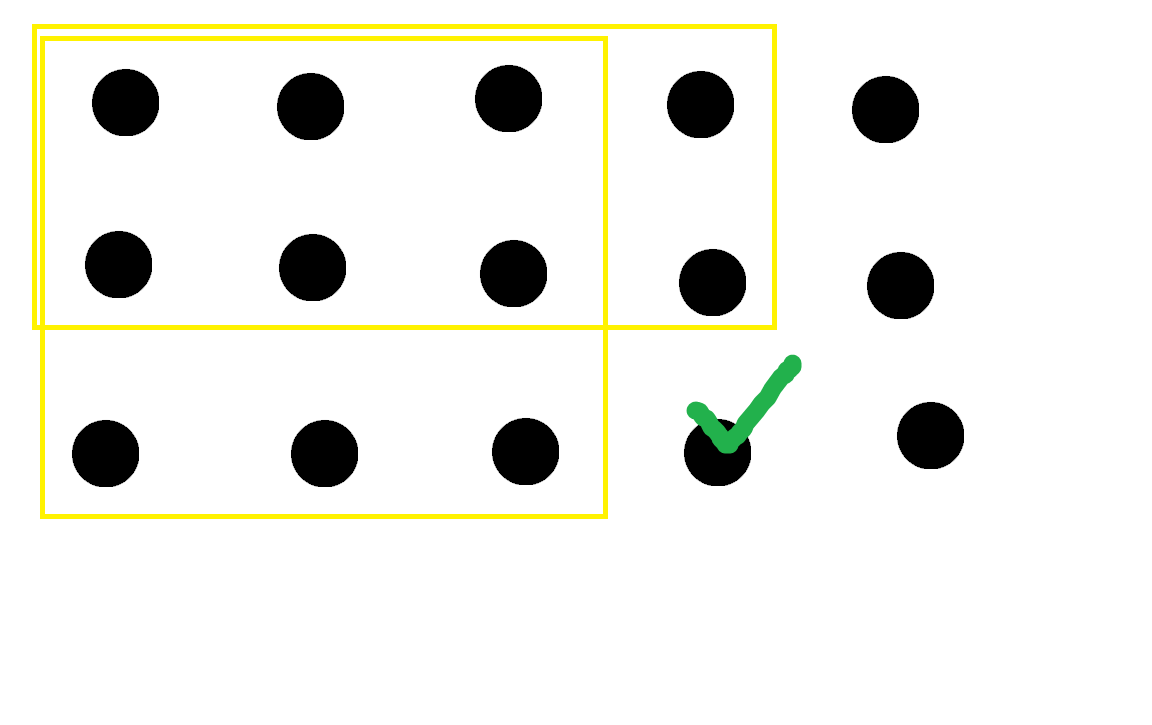
체크 표시가 되어있는 칸을 $(i,j)$라고 할때

이상적인 누적합 $pm(i,j)$는 $(0,0)$부터 $(i,j)$칸까지의 사각형에서

고치는 칸의 개수이다.

왼쪽, 위쪽, 겹치는 칸을 모두 고려해야 하기 때문에,

$pm(i,j)=pm(i,j-1)+pm(i-1,j)-pm(i-1,j-1)$

(단 $i,j>0$)

(0,0)서부터 가로 세로를 먼저 채워주고 (1,1)에서부터 위 점화식을

구현한다.

그렇다면 $K\cdot K$ 범위 내 고쳐야 할 개수는 어떻게 구하는가?

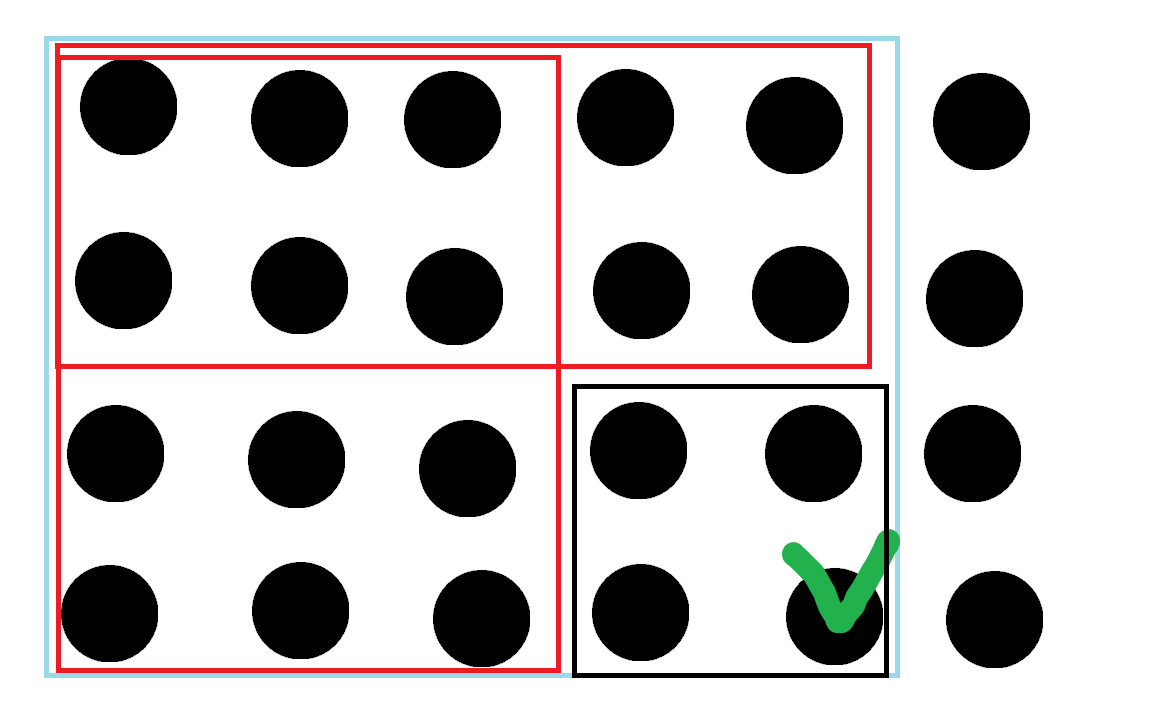
왼쪽, 위쪽을 한번 씩 빼주니 겹치는 부분이 생긴다.

이를 더해주는 점화식은 다음과 같다.

$ans=pm(i,j)-pm(i-k,j)-pm(i,j-k)+pm(i-k,j-k)$

이때 인덱스 에러가 날 수 있는데 이는 $i-k,j-k$가 -1인지 아닌지 확인하여

더해주거나 빼주면 된다.

이를 종합적으로 구현한 코드는 다음과 같다.

#include <bits/stdc++.h>
using namespace std;

int m,n,k,pm[2000][2000][2]={0,},ans=4e6+1;
char board[2000][2000];

int main(){
    ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
    cin >> m >> n >> k;
    for(int i=0;i<m;i++) for(int j=0;j<n;j++) cin >> board[i][j];
    if(board[0][0]=='W') pm[0][0][0]=1;
    else pm[0][0][1]=1;
    for(int i=1;i<m;i++){
        pm[i][0][0]=pm[i-1][0][0];
        pm[i][0][1]=pm[i-1][0][1];
        if(i%2==0){
            if(board[i][0]=='W') pm[i][0][0]++;
            else pm[i][0][1]++;
        }
        else{
            if(board[i][0]=='W') pm[i][0][1]++;
            else pm[i][0][0]++;
        }
    }
    for(int i=1;i<n;i++){
        pm[0][i][0]=pm[0][i-1][0];
        pm[0][i][1]=pm[0][i-1][1];
        if(i%2==0){
            if(board[0][i]=='W') pm[0][i][0]++;
            else pm[0][i][1]++;
        }
        else{
            if(board[0][i]=='W') pm[0][i][1]++;
            else pm[0][i][0]++;
        }
    }
    for(int i=1;i<m;i++) for(int j=1;j<n;j++){
        pm[i][j][0]=pm[i-1][j][0]+pm[i][j-1][0]-pm[i-1][j-1][0];
        pm[i][j][1]=pm[i-1][j][1]+pm[i][j-1][1]-pm[i-1][j-1][1];
        if((i+j)%2==0){
            if(board[i][j]=='W') pm[i][j][0]++;
            else pm[i][j][1]++;
        }
        else{
            if(board[i][j]=='W') pm[i][j][1]++;
            else pm[i][j][0]++;
        }
    }
    for(int i=k-1;i<m;i++) for(int j=k-1;j<n;j++){
        int ld[2]={i,j-k}, rw[2]={i-k,j}, o[2]={i-k,j-k};
        int corValue[2]={0,0};
        if(j>=k && i>=k) for(int l=0;l<2;l++) corValue[l]-=pm[o[0]][o[1]][l];
        if(i>=k) for(int l=0;l<2;l++) corValue[l]+=pm[rw[0]][rw[1]][l];
        if(j>=k) for(int l=0;l<2;l++) corValue[l]+=pm[ld[0]][ld[1]][l];
        ans=min(ans,min(pm[i][j][1]-corValue[1],pm[i][j][0]-corValue[0]));
    }
    cout << ans;
    return 0;
}