평범한 배낭 C++ - 백준 12865

https://acmicpc.net/problem/12865

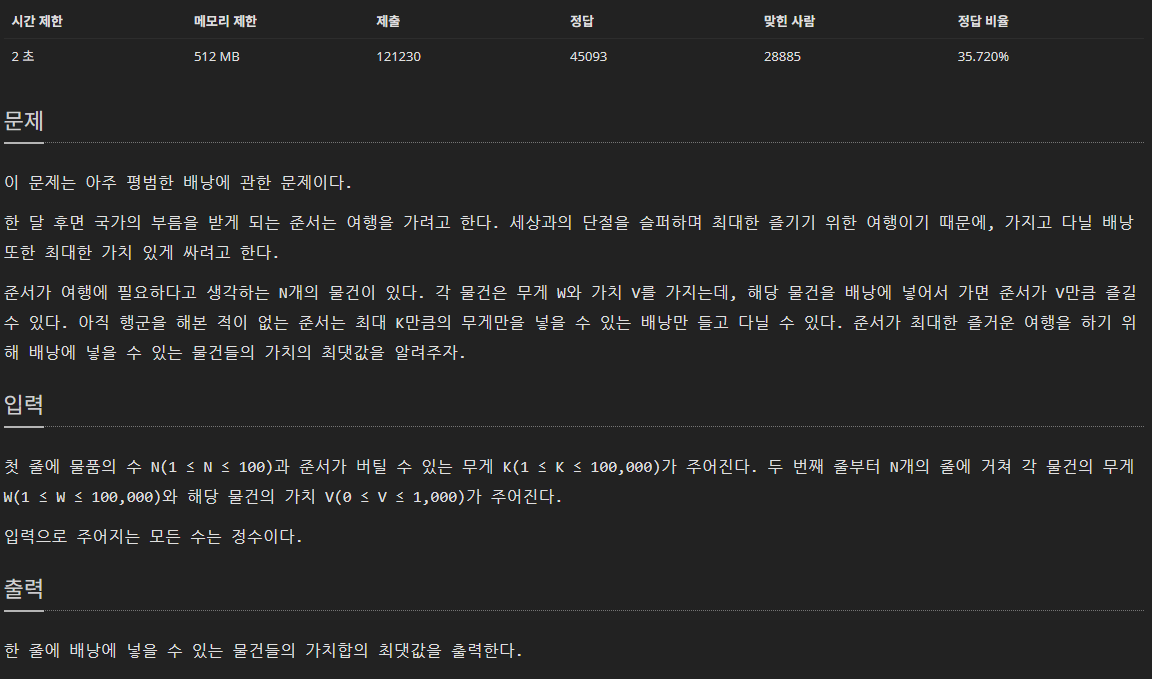
소위 knapsack이라고 불리는 문제이다.

사실 이 문제 유형은 위 문제를 풀면서 알게 되었다.

배낭 문제에 접근할 때 일반적인 dp와 같이 접근했다.

시간 제한이 2초, 물품의 최대 개수가 100, 배낭의 최대 무게가 100,000
이므로 최악의 경우 10,000,000까지라는 것을 생각해보면 O(N^2)이 가능하다.

따라서 K까지의 무게가 되는 경우를 모두 탐색하고 최댓값을
dp 테이블에 저장한다.

코드는 다음과 같다.

#include <bits/stdc++.h>
using namespace std;

vector<pair<int, int>> bag;
bool avail[100001];
int used[100001][101];
int dp[100001];
int N;
int K;
int wv[2];
int j;

int main(){
	ios_base :: sync_with_stdio(false); cin.tie(NULL);
	
	cin >> N >> K;
	avail[0]=true;
	for(int i=0;i<N;i++){
		cin >> wv[0] >> wv[1];
		bag.push_back(make_pair(wv[0], wv[1]));
	}
	for(int i=1;i<=K;i++){
		for(j=0;j<bag.size();j++){
			if(i-bag[j].first>=0 && avail[i-bag[j].first]){
				if(used[i-bag[j].first][j]==0){
					dp[i]=dp[i-bag[j].first]+bag[j].second;
					copy_n(used[i-bag[j].first],101,used[i]);
					used[i][j]++;
					j++;
					avail[i]=true;
					break;
				}
			}
		}
		for(;j<bag.size();j++){
			if(i-bag[j].first>=0 && avail[i-bag[j].first]){
				if(dp[i]<dp[i-bag[j].first]+bag[j].second){
					if(used[i-bag[j].first][j]==0){
						dp[i]=dp[i-bag[j].first]+bag[j].second;
						copy_n(used[i-bag[j].first],101,used[i]);
						used[i][j]++;
						avail[i]=true;
					}
				}
			}
		}
	}
	sort(dp,dp+K+1);
	cout << dp[K];
}

무게를 K까지 탐색할때에 물품의 무게로 만드는게 불가능한 경우까지 따져야 했고, 물품이 사용되었는지도 따져야 하는 문제였다.