하노이 탑 이동 순서 C++ - 백준 11729

https://www.acmicpc.net/problem/11729

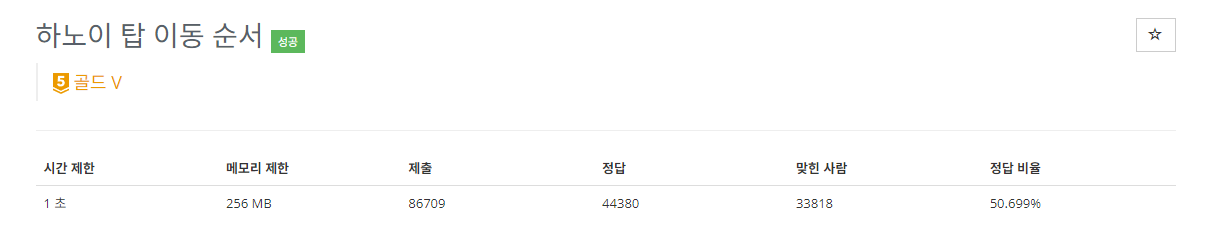
하노이탑 문제.

하노이탑 설명

하노이탑의 규칙 특성상 가장 아래에 있는 원판을 옮기려면 위 원판을 옮겨야 한다.

이 논리는 원판의 크기가 2인 원판까지 통해 재귀적으로 실행이 가능하다.

1. 어떻게 원판을 옮기는가

일단 하노이탑의 본질적 목표를 보면 1번째 기둥에 있는 n개의 원판을

3번째 기둥으로 옮기는 것이다.

위 하노이탑 논리에 의하여 n번째는 n-1번째의 이동을,

n-1번째는 n-2번째의 이동을 필요로 한다.

$n=3$일때를 예시로 보자

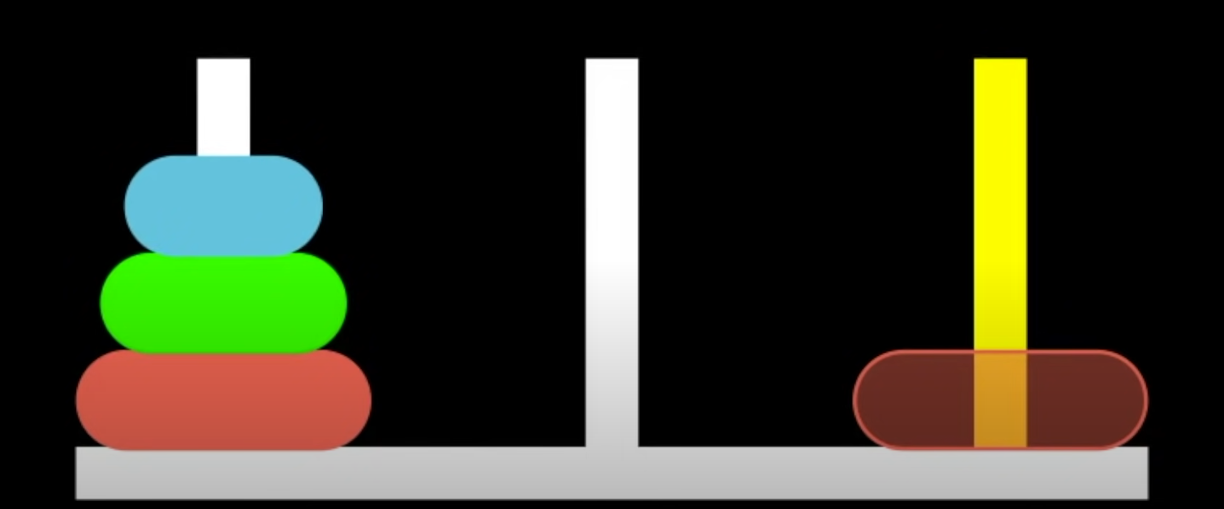
3번째 원판을 목표 지점으로 옮기기 위해서는

1,2번째 원판을 2번째 기둥으로 옮겨야 한다.

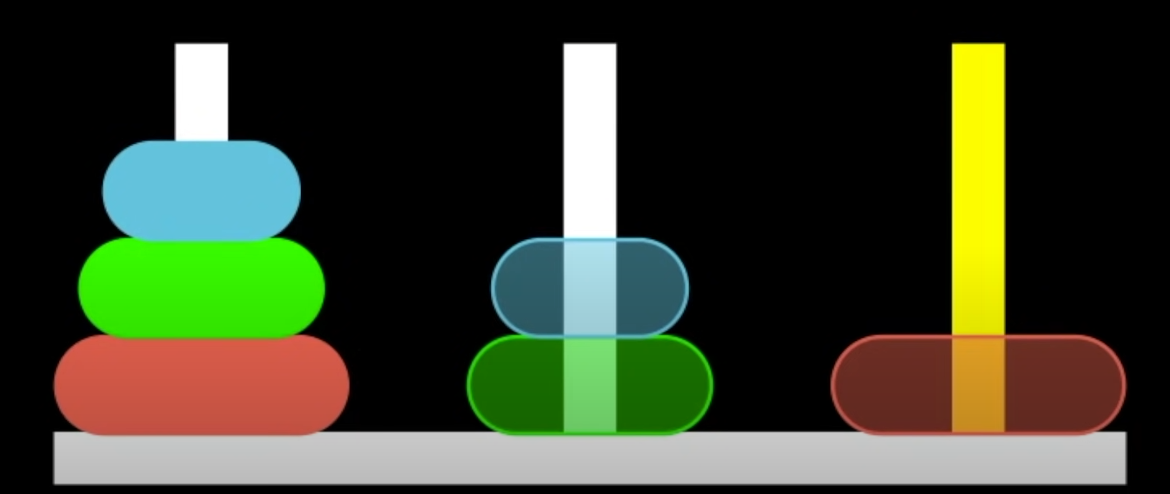
그리고 2번째 원판을 2번째 기둥으로 옮기기 위해서는

1번째 원판을 3번째로 옮겨야 한다.

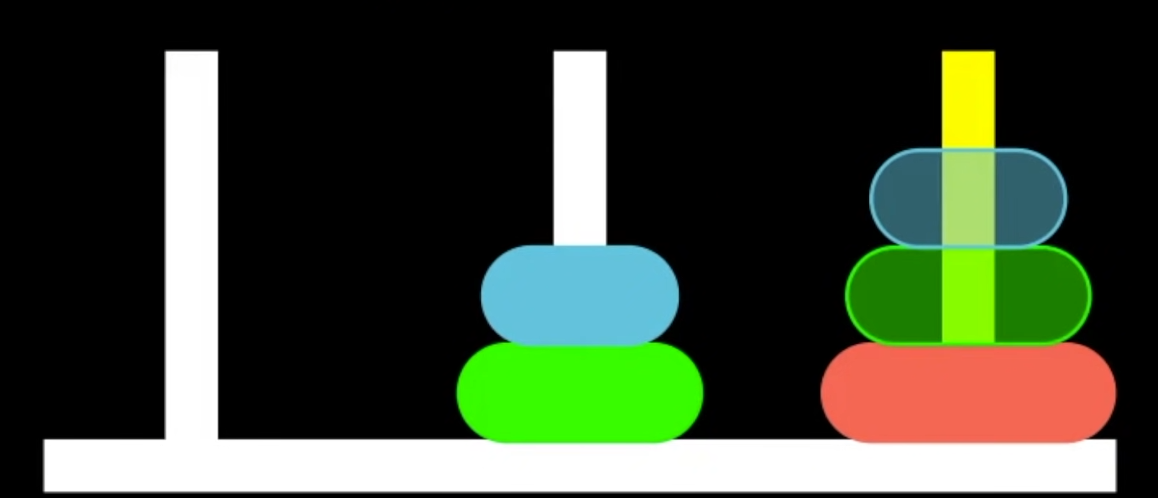
그 다음은 합치는 과정이 필요하다.

2번째 원판과 1번째 원판을 3번째 기둥으로 옮기려면 1번째 원판을

1번째 기둥으로 옮기고 2번째 원판을 3번째로,

1번째 원판으로 3번째로 옮기면 된다.

따라서 $n$번째$(n!=1)$ 원판을 옮기려면 $n-1$번째 원판을

다른 곳으로 옮기는 이동 $1$

합치는 이동 $2$가 필요하다.

따라서 옮기는 횟수 $t_n = 2\cdot t_{n-1} + 1$ 이다.

원판이 하나만 있을때 이동횟수가 1이므로,

이를 단항식으로 만들게 되면,

$t_n=2^n-1$이다.

이를 구현한 코드는 다음과 같다.

#include <bits/stdc++.h>
using namespace std;

int n;

void h(int n, int from, int to, int other){
    if(n==1){cout << from << ' ' << to << '\n';return;}
    h(n-1,from,other,to);
    cout << from << ' ' << to <<'\n';
    h(n-1,other,to,from);
}

int main(){
    ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
    cin >> n;
    cout << int64_t(pow(2,n))-1 << '\n';
    h(n,1,3,2);
    return 0;
}