합분해 C++ - 백준 2225

https://www.acmicpc.net/problem/2225

이 문제는 dp 점화식 세우기가 매우 어려웠다.

먼저 점화식을 세우기 전 수들의 규칙부터 살펴야 하는데,

이를 정리하면 다음과 같다.

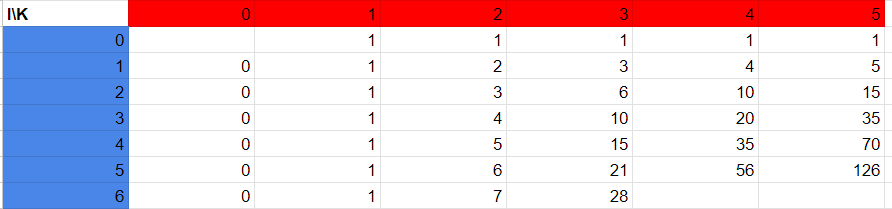
K개의수로 I를 만드는 경우의 수를 나타낸 표다.

위를 살펴보면 i를 k개로 만드는 경우의 수는

i-1개를 1개부터 k로 만드는 경우의 수의 합과 같다는 것을 알 수 있다.

$dp[n][k] = \sum_{j=1}^K dp{[n-1][j]}$

이를 더 줄여서 표현할 수 있는데 그 이유는 $dp[n][k-1]$이

$\sum_{j=1}^{K-1} dp{[n-1][j]}$을 담고 있기 때문에

$dp[n][k] = dp[n][k-1]+dp[n-1][k]$로 표현된다.

코드는 다음과 같다.

#include <bits/stdc++.h>
#define MOD 1000000000
using namespace std;

int n,k;
long long dp[201][201];

int main(){
    cin >> n >> k;
    for(int i=1;i<=k;i++){
        dp[0][i]=1;
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=k;j++){
            dp[i][j]=(dp[i][j-1]+dp[i-1][j])%MOD;
        }
    }
    cout << dp[n][k];
    return 0;
}