
앞으로 돈에 관련된 프로젝트를 맡게 될 예정이라 조금 찾아보다보니
BigDecimal자료형을 사용해야한다고 한다.
DataSize를 사용하는것처럼 직관적이게 사용하기위해 그런걸까 싶어서 관련 내용을 조금 찾아봤다.
java에서 실수(mistake 아님)를 표현하는 방식으로 double, float 등을 사용할수있다. 그런데 이녀석들은 정확하지 않다.
double
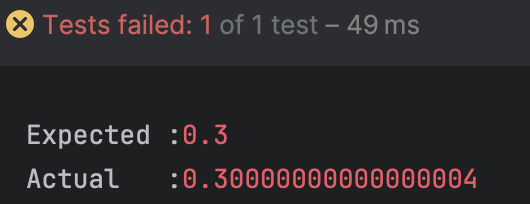
0.1 과 0.2를 더하면 0.3이 된다.
아주 간단한 테스트다.
@Test
void wrong_double_test(){
double a = 0.1;
double b = 0.2;
assertThat(a + b).isEqualTo(0.3);
}아니, 틀렸다!
float
그렇담 이건 어떨까
0.1을 100번 더한다!
그렇담 당연히 10이 아닐까?
@Test
void wrong_float_test(){
float result = 0f;
for(int i = 0; i < 100; i++){
result += 0.1f;
}
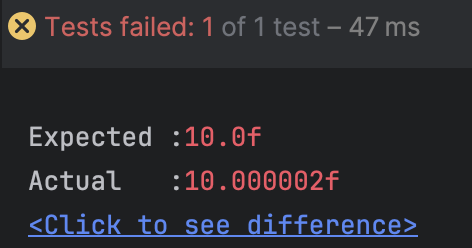
assertThat(result).isEqualTo(10f);
}그렇게 생각했다면 역시 틀렸다!
10진수를 2진수로~
정수부
위와같은 실수 타입의 계산은 2진법을 사용하는 컴퓨터의 이슈로 생각하면 된다.
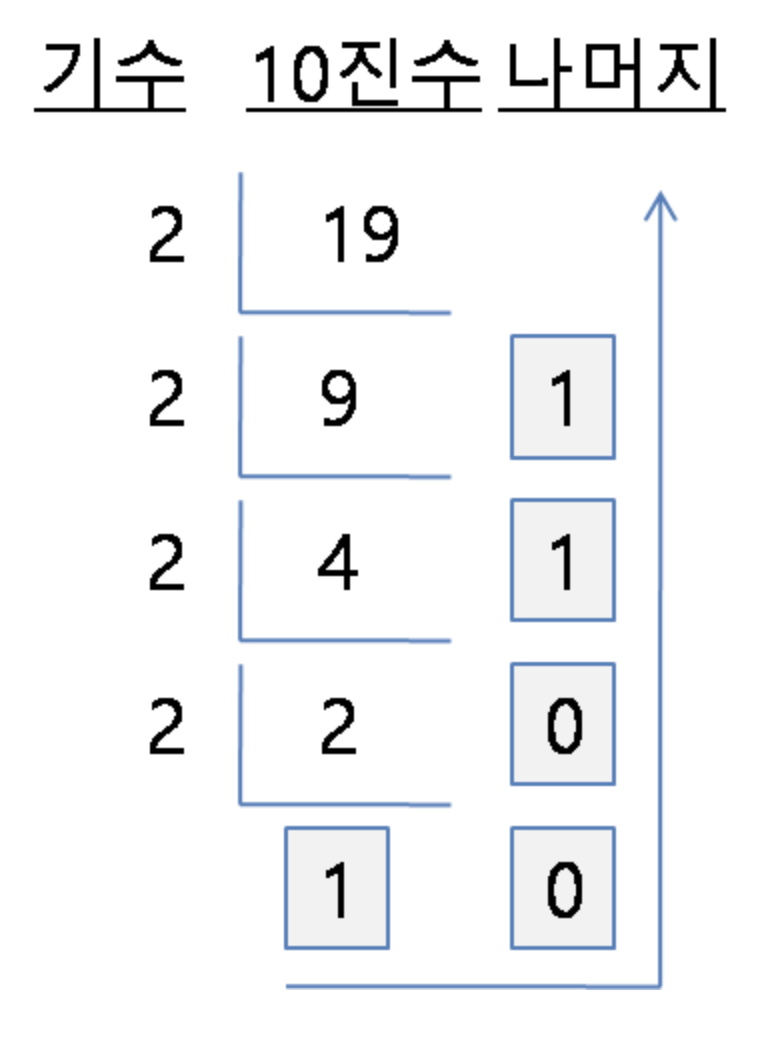
그러니깐 간단히 예를들면, 정수부는 다음 그림처럼 2진수로 깔끔하게 떨어질수있게 표현할수있다. (10진수 19를 2진수로 바꾸는 작업! )
소수부
그렇다면 소수부를 10진수에서 2진수로 변환해보자.
10진수를 2진수로 변환할때 정수부에서는 2를 나누어준것처럼, 소수부에서는 2를 곱하여 나오는 정수를 차례로 쓰는걸로 변환을 할수있다.
10진수 0.625 를 2진수로 변환하는 과정은 다음과 같다.
1) 0.625 * 2 = 1.250 > 1
2) 0.250 * 2 = 0.50 > 0
3) 0.50 * 2 = 1.0 > 1
깔끔하게 10진수 0.625는 2진수 0.101로 변환되는것을 확인했다.
하지만 아주 운이 좋았다고 할수있다.
동일한 방법으로 10진수 0.1을 2진수로 변환해보자.
1) 0.1 * 2 = 0.2 > 0
2) 0.2 * 2 = 0.4 > 0
3) 0.4 * 2 = 0.8 > 0
4) 0.8 * 2 = 1.6 > 1
5) 0.6 * 2 = 1.2 > 1
6) 0.2 * 2 = 0.4 > 0
...동일하게 구하려고 했는데 2단계에서 나온 0.2가 6단계에서도 동일하게 나온걸 본다면 깔끔하게 떨어지지 않고 다음과 같이 구질구질하게 나올 예정이다.
0.1₍₁₀₎ = 0.000110011001100...₍₂₎
여기에서 위 테스트가 실패한 이유를 알 수 있다. 컴퓨터는 제한된 메모리에 데이터를 저장하기 때문에, 2진수로 변환했을때 무한소수로 나오는 값들은 근사값을 저장하게 된다.

고정소수점과 부동소수점 용어정리
일단 용어부터 정리를 하겠다. 고정 과 부동 은 같은말처럼 생겨서 헷갈린다...
- 고정(固定)

- 부동(浮動)

고정소수점
- 간단하게 설명하고 넘어가겠다. 저장할 공간에 정수부를 저장하는 비트와 실수부를 저장하는 공간이 고정되어있다는것.
- 예를들면 다음 그림은 32bit를 저장하는 공간에서 정수부에는 16bit만큼, 소수부에는 15bit만큼 넣겠다고 고정한 자료형이 되겠다.

- 하지만 숫자를 사용하다보면 아주 큰수를 사용할때가 있고, 소수점으로 아주 세밀하게 사용할 때도 있기때문에 해당 메모리를 효율적으로 사용할 수 없을때가 있다.
부동소수점
- 그래서 컴퓨터에서는 메모리를 효율적으로 사용하기 위해 부동소수점 방식을 택하게 된다.
- 일단 부동소수점을 사용한다라는건
정규화에 대해 알아야하는데,2진법으로 변환하여 정수부를 1로 만든다!라고 생각해주면 좋을것 같다.
10진수 19.125 를 2진수로 변환하여 정규화를 해보자!
19.125₍₁₀₎
= 10011.001₍₂₎
= 1.0011001₍₂₎ * 2⁴ << 이게 정규화된거다!정규화된 1.0011001₍₂₎ * 2⁴ 를 IEEE 754 표준에 맞게 넣어보자.
일단 IEEE 754의 메모리 할당은 다음 그림과 같다.

부호 비트, 지수 비트, 가수 비트의 계산은 다음과 같다.
1) 양수/음수에 따라 부호 비트에 넣는다
- 양수 : 0
- 음수 : 1
2) 자릿수를 나타내는 2⁴의 지수인 4와 127을 더하여 지수 비트에 넣는다.
- 127₍₁₀₎ = 01111111₍₂₎
3) 소수 부분은 가수 비트에 차례대로 넣는다.
- 0.0011001₍₂₎
계산 결과값은 다음과 같다
(부호) (지수) (소수)
0 10000011 00110010000000000000000다른 언어에서는 어떤걸 쓰나
2진수로 표현했을때 무한소수를 표현할 수 없어서 위와같은 이슈가 있는걸 알아봤다.
그리고 다른 언어에서도 세밀한 실수를 표현하기위해서는 사용하는 대체제가 따로 존재하는것 같다.
| 언어 | 대체 |
|---|---|
| Java | BigDecimal |
| javascript | big.js |
| python | decimal |
