만유인력의 법칙

만유인력의 법칙 공식은 아래와 같다.

F = G * m1 * m2 / r ²

G = 6.673 × 10 ^ (−11) = 6.673e-11 (J * M /(kg^2))

---

지구와 달에 대한 데이터

지구와 달에 대한 데이터를 아래에 나열하겠다.

지구의 질량

5.972 × 10^24 = 5.972e24 (kg)

달의 질량

7.36 * 10^22 = 7.36e22 (kg)

지구의 반지름

6371000 (m)

달의 반지름

1737100 (m)

지구와 달의 거리

385000000 (m)

---

만유인력 코드

from random import randint
from vpython import *

earth = sphere(pos=vec(0, 0, 0), radius=6400000, texture=textures.earth)
moon = sphere(pos=vec(385000000, 0, 0), radius=1737100,
              texture=textures.rock, make_trail=True)

# 지구와 달의 확대를 위한 설정
earth.radius = 6 * earth.radius
moon.radius = 6 * moon.radius

# 각종 상수
G = 6.673e-11
earth.m = 5.972e24
moon.m = 7.347e22

# 초기 속도 설정
earth.v = vec(0, 0, 0)
moon.v = vec(0, 0, 0)

# 1 프레임당 시뮬레이션에서는 60초가 지나간다는 설정
# 즉, rate(1000)일 때 1초가 지나면 60000초가 지남 
t = 0
dt = 60

while True:
    rate(1000)

    r = moon.pos - earth.pos

    # 만유인력 법칙과 작용과 반작용의 법칙
    moon.f = -G * earth.m * moon.m/mag(r)**2*norm(r)
    earth.f = -moon.f

    # F = m*a를 이용해 a 구하기
    moon.v = moon.v + moon.f/moon.m * dt
    earth.v = earth.v + earth.f/earth.m * dt

    moon.pos = moon.pos + moon.v * dt
    earth.pos = earth.pos + earth.v * dt

    t = t + dt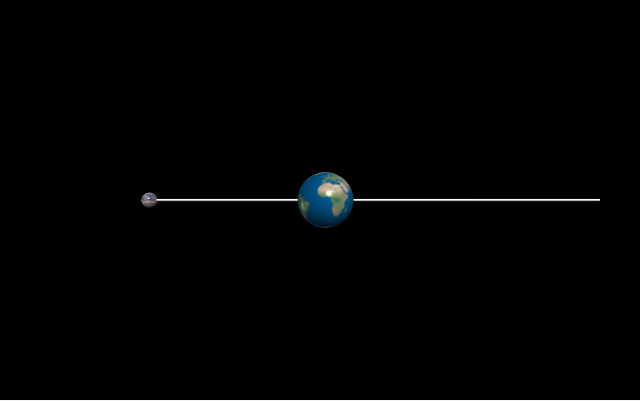

이 코드를 실행하면 지구와 달이 서로에게 가까워지는 시뮬레이션을 출력한다.

이는 달의 공전을 표현하고 있지 않기 때문에, 우리가 원했던 시뮬레이션이 아니다.

이는 지구와 달의 초기 속도가 0으로 설정되어 만유인력에 의해 서로에게 가까워질 수밖에 없기 때문이다.

달의 공전을 표현하기 위해서는 달의 초기 속도의 방향을 지구로의 방향과 수직이 되게 설정하면 된다.

---

달의 공전 코드

달의 공전 속도

1022 (km/s)

이를 달의 초기 속도에 적용하기만 하면 된다.

추가로, 만유인력은 지구와 달 모두에게 적용되기 때문에, 지구 역시 달에 끌려가면서 달의 공전 궤도가 지구의 위치 변화에 따라 조금씩 바뀌게 된다.

이를 해결하기 위해서는, 지구의 초기 속도를 달과 반대 방향으로 (달의 공전 속도 * 달의 질량 / 지구의 질량) 크기만큼 설정해주면 달의 궤도가 더 일정하게 된다.

전체 코드

from random import randint
from vpython import *

earth = sphere(pos=vec(0, 0, 0), radius=6400000, texture=textures.earth)
moon = sphere(pos=vec(385000000, 0, 0), radius=1737100,
              texture=textures.rock, make_trail=True)

# 지구와 달의 확대를 위한 설정
earth.radius = 6 * earth.radius
moon.radius = 6 * moon.radius

# 각종 상수
G = 6.673e-11
earth.m = 5.972e24
moon.m = 7.347e22

# 초기 속도 설정
earth.v = vec(0, -1022, 0)
moon.v = vec(0, 1022, 0)

# 1 프레임당 시뮬레이션에서는 60초가 지나간다는 설정
# 즉, rate(1000)일 때 1초가 지나면 60000초가 지남 
t = 0
dt = 60

while True:
    rate(1000)

    r = moon.pos - earth.pos

    # 만유인력 법칙과 작용과 반작용의 법칙
    moon.f = -G * earth.m * moon.m/mag(r)**2*norm(r)
    earth.f = -moon.f

    # F = m*a를 이용해 a 구하기
    moon.v = moon.v + moon.f/moon.m * dt
    earth.v = earth.v + earth.f/earth.m * dt

    moon.pos = moon.pos + moon.v * dt
    earth.pos = earth.pos + earth.v * dt

    t = t + dt