1. Counting Sort란?
Counting Sort는 이름 그대로 카운팅하면서 정렬을 진행하는 알고리즘이다.
무엇을 카운팅하나면 바로 각 수의 개수를 카운팅하여 다른 배열에 저장하는 것이다.
각 수를 카운팅하여 배열에 저장한 뒤 해당 배열에 개수만큼 배열을 재배치하는 방식이다.
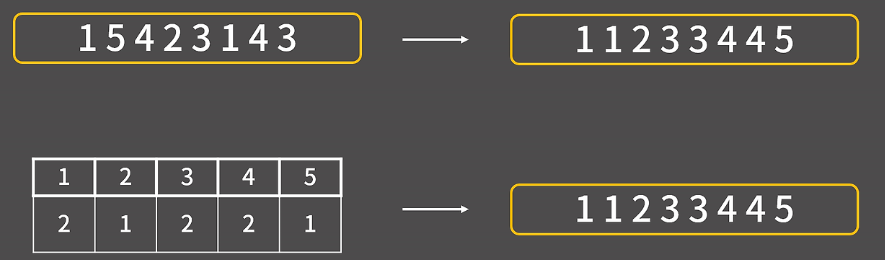
위 그림을 보면 쉽게 이해가 될 것이다.
동작 방식
1) 각 숫자의 등장 횟수를 저장할 카운팅 배열을 선언한다.
2) 배열에 저장된 값만큼 원소를 출력한다.
2. 코드
#include <bits/stdc++.h>
using namespace std;
int cArr[1000002]; //Counting Array
int n;
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int num;
cin >> n;
for(int i=0; i<n; i++)
{
cin >> num;
cArr[num]++;
}
for(int i=1;i<1000002;i++)
{
while(cArr[i]--) cout << i << ' ';
}
return 0;
}
// 입력 결과
// 13
// 59 5 9 21 17 9 3 5 2 2 1 6 4
// 출력 결과
// 1 2 2 3 4 5 5 6 9 9 17 21 59 3. 특징
1) 구현이 간단함
Counting Sort는 비교 기반 정렬과 달리 간단한 배열 연산만으로 정렬을 수행할 수 있어 구현이 매우 쉽다.
2) 추가 메모리 필요
각 숫자의 등장 횟수를 저장하기 위한 Counting Array가 필요하므로, 추가적인 메모리를 사용한다.
3) 제한된 숫자 범위에서 효율적
Counting Sort는 원소의 범위가 크지 않을 때 효과적이다. 하지만 범위가 지나치게 넓으면 큰 크기의 배열이 필요하여 메모리 낭비가 심해질 수 있다.
4) 비교 정렬이 아님
일반적인 정렬 알고리즘과 달리 요소 간의 비교 연산을 수행하지 않고, 단순한 카운팅을 통해 정렬을 진행한다.
4. 마무리
Counting Sort는 특정 범위의 정수를 정렬할 때 매우 빠르고 효율적이지만 메모리 사용량이 많아질 수 있는 단점이 있다. 따라서 원소의 값이 제한적인 경우에 적합하며 범위가 넓은 경우에는 다른 정렬 알고리즘을 고려하는 것이 좋다.
Reference
[실전 알고리즘] 0x0F강 정렬II - BaaaaaaaarkingDog
