Dynamic Programming

1. Dynamic Programming이란?

Dynamic Programming(DP)은 문제를 여러 개의 하위 문제를 나눈 뒤 결과를 쌓아 올려 동일한 계산을 반복하지 않도록 하는 알고리즘이다.

대표적인 예시로는 피보나치 수열이 존재한다.

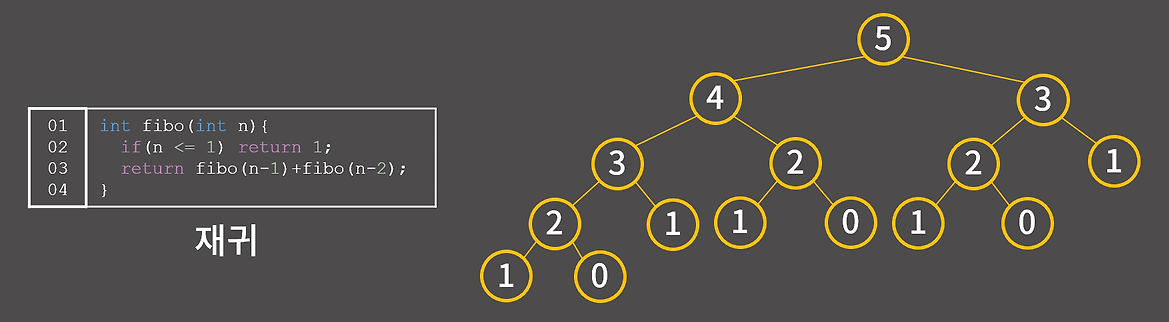
이처럼 피보나치를 재귀를 통해 구현할 수 있지만, F(5)를 구하기 위해 F(4) + F(3)를 구해야 한다. 그러나 F(4)를 구하려면 F(3) + F(2), F(3)을 구하려면 F(2) + F(1)을 계산해야 하는 식으로 중복 연산이 계속 발생하여 비효율적인 계산이 된다. 이 경우, 시간 복잡도는 O(1.618^N)으로 매우 비효율적이다.

이러한 중복 연산 문제를 DP를 활용하여 해결할 수 있다.
피보나치의 F(5)를 구하기 위해 초깃값인 F(0)과 F(1)를 설정한 뒤 그 뒤로는 점화식을 설정하여 F(2), F(3),..., F(N)을 차례로 구하여 O(N) 시간 복잡도로 해결할 수 있다.

DP를 구현하기 위한 3가지 요소
1. 테이블 정의하기
테이블은 DP가 결과를 쌓아 올려 문제를 해결하는 알고리즘이라 설명했듯이,
각 문제를 해결한 결과를 저장할 테이블을 정의해야 한다.
피보나치로 예시를 들자면, k번째 값을 구할 때 결과가 무엇인지 정의하는 테이블 F(K)를 설정할 수 있다.
// F(K) = K번째 피보나치 수열의 결과
2. 점화식 찾기
점화식은 말 그대로 위에서 정의한 테이블에 값을 넣어주기 위한 식을 찾는 과정이다.
피보나치의 수열 공식은 이전값과 그 이전값을 더한 값이므로 F(K) = F(K-1) + F(K-2)라는 점화식을 알 수 있다.
3. 초깃값 설정하기
테이블과 점화식을 다 정의했다면, 이제 초깃값만 설정해 주면 된다.
피보나치에서 F(1) = F(0) + F(-1)는 없으므로 F(1)과 F(0)의 값을 미리 지정해 주고 인덱스를 F(2)부터 점화식을 적용하면 된다.

2. 코드(피보나치)

#include <bits/stdc++.h>
using namespace std;

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	
	int F[20];
	int n ;
	cin >> n;
	
	F[1] = F[0] = 1;
	
	for(int i=2; i<=n; i++)
		F[i] = F[i-1] + F[i-2];
	
	cout << F[n];	
	
	return 0;
}

// 입력
// 5 

// 출력
// 8

3. 특징

1. 중복 계산을 줄임
   DP를 사용하면 기존의 재귀 방식과 달리 동일한 값을 여러 번 계산하지 않으므로 성능이 향상된다.
2. 탑다운(메모이제이션) vs. 바텀업(반복문) 접근 방식
   탑다운 방식: 재귀 호출과 메모이제이션을 활용해 필요할 때만 계산한다.
   바텀업 방식: 반복문을 사용해 작은 문제부터 차례대로 해결한다.

4. 마무리

DP는 중복된 연산을 줄이고 최적의 해를 구하는 데 유용한 알고리즘이다. 특히 피보나치 수열처럼 동일한 부분 문제가 반복되는 경우 DP를 활용하면 큰 성능 향상을 얻을 수 있다. 이후에는 DP를 활용한 다양한 문제(예: 배낭 문제, LIS 등)를 풀면서 공부해 보려 한다.

Reference
[실전 알고리즘] 0x10강 다이나믹 프로그래밍 - BaaaaaaaarkingDog