Merge Sort

알고리즘에서 정렬 파트 중 선택, 삽입, 버블 정렬 이후 퀵 정렬과 병합 정렬을 배웠던 걸로 기억한다. 그때 당시에는 복잡하고 뭔말인지 잘 이해를 못했었는데 다시 공부해 보니 그때 느꼈던 만큼 복잡하거나 어렵진 않은 파트인듯하다.

1. Merge Sort란?

Merge Sort(병합 정렬)는 분할 정복(Divide and Conquer) 방식을 사용하는 정렬 알고리즘이다. 이 알고리즘을 이해하기 위해 먼저 정렬 과정이 어떻게 진행되는지 살펴보자.

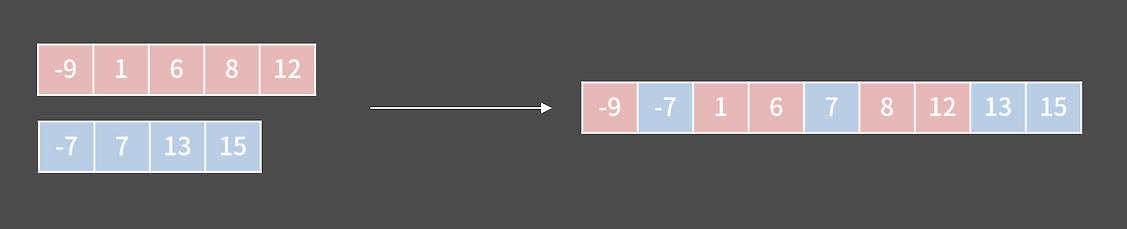
먼저 그림을 보면 두 배열은 각각 정렬된 상태이고 오른쪽은 두 배열을 합쳐 정렬된 상태이다. 왼쪽의 두 배열을 오른쪽 배열로 합치는데 걸리는 시간 복잡도를 계산해 보자.
두 배열의 크기가 각각 N,M이라고 가정할 때 오른쪽 배열 첫 번째에 가장 작은 원소가 와야 하므로 N+M개를 다 봐야 할 필요가 있을지 보자. 보다싶이 각 배열은 정렬이 된 상태이므로 맨 앞에가 제일 작은 수임을 알 수 있다. 그렇다면 오른쪽 배열 맨 앞에 올 숫자는 두 배열의 맨 앞의 값을 비교하여 더 작은 수를 넘겨주면 되므로 이 비교 횟수는 O(1)이다.
그렇게 배열마다 맨 앞자리를 비교하여 더 작은 수를 넘겨주면 되므로 총시간 복잡도는 O(N+M)이 된다.

(각 배열의 맨 앞 순서대로 비교하여 채워 넣는 과정)

이처럼 두 개의 정렬된 배열을 병합하는 것이 Merge Sort의 핵심 과정이다. 이제 배열을 분할하는 과정도 살펴보자.

Merge Sort는 주어진 배열을 반씩 나누는 분할 과정과 병합을 통해 정렬하는 과정으로 구성된다.
배열의 길이가 1이 될 때까지 재귀적으로 나눈 뒤 다시 병합하면서 정렬을 수행한다.

분할 과정은 다음과 같이 이루어진다.

• 배열을 중간을 기준으로 두 부분으로 나눈다.
• 왼쪽 부분과 오른쪽 부분에 대해 각각 Merge Sort를 재귀적으로 호출한다.
• 배열의 크기가 1이 되면 병합을 진행한다.

간단하게 이런 식으로 정리할 수 있으며 병합 과정은 위에 알고리즘과 동일하다.
따라서 코드는 다음과 같이 구현할 수 있다.

2. 코드

#include <bits/stdc++.h>
using namespace std;

int n = 11;
int arr[1000002] = {3, 7, 12, 21, 4, -6, 5, -8, -2 ,0, 11};
int temp[1000002];

void merge(int st, int en)
{
	int mid = (st+en)/2;
	int lidx = st;
	int ridx = mid;
	
	for(int i=st; i<en; i++)
	{
		if(lidx == mid) temp[i] = arr[ridx++];
		else if(ridx == en) temp[i] = arr[lidx++];
		else if(arr[lidx] < arr[ridx]) temp[i] = arr[lidx++];
		else temp[i] = arr[ridx++];
	}
	
	for(int i=st; i<en; i++) arr[i] = temp[i];
}

void merge_sort(int st, int en)
{
	if(st+1 == en) return;
	
	int mid = (st+en)/2;
	merge_sort(st, mid);
	merge_sort(mid, en);
	merge(st,en);
}

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	
	merge_sort(0,n);
	
	for(int i=0; i<n; i++) cout << arr[i] << ' ';
	
	return 0;
}

// 출력결과
// -8 -6 -2 0 3 4 5 7 11 12 21 

3. 특징

1) 시간 복잡도
Merge Sort의 시간 복잡도는 O(NlogN)이다. 이는 대부분의 상황에서 안정적인 성능을 보장한다.

2) Stable Sort(안정 정렬)
Merge Sort는 안정 정렬(Stable Sort)이다. 즉, 같은 값을 가진 요소들이 정렬 전후에도 순서가 유지된다.
예를 들어 사람 데이터를 나이순으로 정렬한 후 같은 나이일 경우 이름순으로 유지되도록 정렬할 때 유용하다. 2차원 좌표 (x, y)를 정렬하는 경우에도 사용된다.

3) 공간 복잡도
Merge Sort는 추가적인 배열을 사용하여 정렬을 수행하므로 O(N)의 추가 공간이 필요하다. 따라서 메모리 사용이 중요한 환경에서는 다른 정렬 알고리즘(예: Quick Sort)이 더 적합할 수 있다.

4. 마무리

Merge Sort는 분할 정복 기법을 이용해 의 시간 복잡도를 가지는 강력한 정렬 알고리즘이다. 특히 안정 정렬이 필요한 경우 유용하며 정렬해야 할 데이터 크기가 클수록 성능이 뛰어나다. 하지만 추가적인 메모리 사용이 필요하다는 단점도 고려해야 한다.

Reference
[실전 알고리즘] 0x0E강 정렬I - BaaaaaaaarkingDog