예전에 닌텐도로 역전 재판을 즐겨 했던 적이 있었다. 게임을 하면 다양한 선택지가 나오는데 매번 틀려 맞을 때까지 선택지를 골랐다. 이 얘기를 하는 이유는 바로 백트래킹과 관련이 있기 때문이다.
1. 백트래킹이란?
백트래킹은 현재 상태에서 가능한 모든 후보군을 따라 탐색하며 최적의 해를 찾는 알고리즘이다. 간단히 말해 가능한 선택지 중 하나를 선택하고 이를 반복하면서 해답을 찾는다. 만약 선택이 실패하거나 불가능한 경우에는 이전 상태로 돌아가 다른 선택지를 탐색하는 방식이다. 이 알고리즘의 대표적인 예시 중 하나가 오목이다.
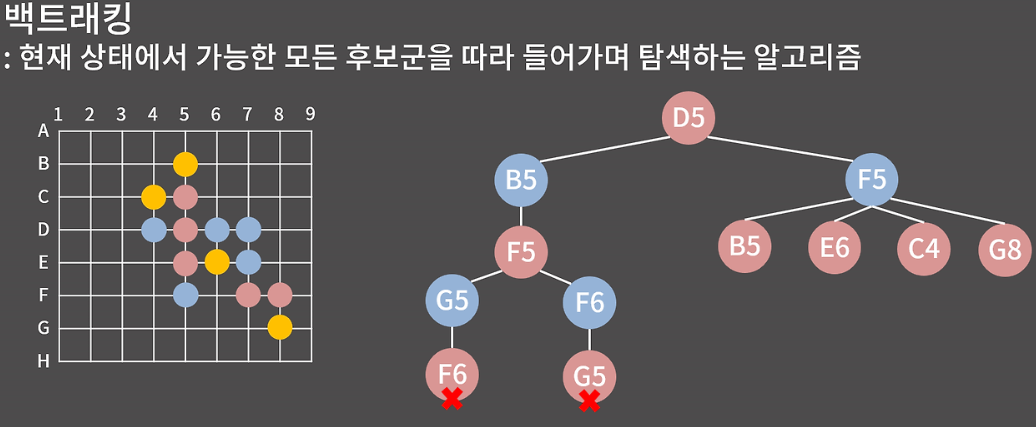
예를 들어, 오목에서 파란 돌을 두는 상황을 가정해 보자. 현재 빨간 돌이 D5에 놓여 있고, 파란 돌로 이를 막아야 한다. 만약 B5에 돌을 두면 빨간 돌이 4-3 상태를 만들 수 있으므로 이는 패배로 이어질 수 있다. 따라서 B5에 두는 선택지는 제거되고, 다른 가능한 위치인 F5에 돌을 두는 것이 적합하다. 이후 빨간 돌의 차례에서 가능한 모든 공격 경로를 계산하고 이를 반복하며 최적의 수를 찾는 과정이 바로 백트래킹이다.
2. 특징
백트래킹의 정의는 이해했으니, 이를 어떤 상황에서 사용하는지 알아보자. 백트래킹은 탐색 과정에서 이전 상태의 정보가 필요한 경우에 유용하다. 위의 오목 예시처럼, D5에서 시작해 F6까지 진행한 결과가 패배를 나타내는 경우, 굳이 처음부터 다시 시작할 필요 없이 F5의 상태로 돌아와 다른 선택지를 탐색하는 것이 더 효율적이다.
- 장점
가지치기 (Pruning)
백트래킹은 더 이상 탐색할 필요가 없는 상태를 제외하는 방식으로 효율성을 높인다.
예를 들어 오목에서 상대방이 3목을 만들었다면 돌을 둘 곳은 공격 경로와 방어 경로로 제한된다. 모든 경우를 탐색하지 않고도 필요한 위치만 계산할 수 있다.
모든 해 탐색
백트래킹은 가능한 모든 해를 탐색하는 과정을 통해 최적의 해를 찾아낸다. 이를 통해 문제가 복잡하더라도 정확한 해답을 보장할 수 있다.
- 단점
비효율성 (해가 없는 경우)
탐색 공간이 매우 크고 해가 존재하지 않을 경우에는 시간과 연산 자원을 비효율적으로 사용할 수 있다.
메모리 사용량
탐색 과정에서 상태를 저장하기 위해 많은 메모리가 필요하다. 이는 문제의 크기가 클수록 심각한 부담이 될 수 있다.
3. 마무리
백트래킹은 문제 해결을 위해 기본적인 논리와 알고리즘의 흐름을 이해하는 데 중요한 개념이다. 하지만 이를 실제로 잘 활용하려면 다양한 문제를 풀어보며 실전 감각을 익히는 것이 중요하다. 현재는 Unity 관련 기능을 조사하는 것이 우선이므로 백트래킹에 대한 정리는 여기서 마무리하자. 추후 이 글의 내용에서 수정하거나 보완할 부분이 발견되면 다시 다루기로 하자.
Reference
[실전 알고리즘] 0x0C강 백트래킹 - BaaaaaaaarkingDog
