이진 검색 트리란?
먼저 트리(Tree)란 부모 노드가 존재하고, 그 아래에 자식 노드가 연결된 계층적인 구조를 가진 그래프를 말한다. 트리의 최상단 노드를 루트(Root) 노드라고 부르며 각 노드는 0개 이상의 자식 노드를 가질 수 있다.
여기서 이진 트리(Binary Tree)란 모든 노드가 최대 2개의 자식 노드를 가지는 트리를 의미한다. 자식 노드는 보통 왼쪽(Left)과 오른쪽(Right)으로 구분된다.
각 노드의 자식이 2개 이하이므로 왼쪽과 오른쪽 자식으로 구분이 가능하다.
이 정도면 이진 검색 트리에 대하여 설명이 가능하다.
- 왼쪽 서브트리에 있는 모든 노드의 값은 부모 노드보다 작다.
- 오른쪽 서브트리에 있는 모든 노드의 값은 부모 노드보다 크다.
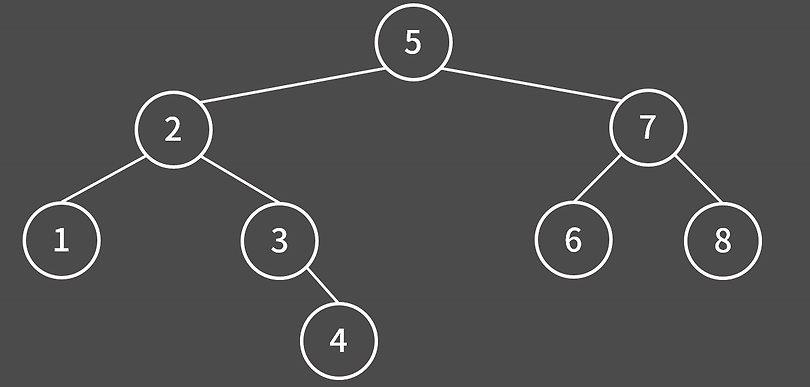
해당 이진 검색 트리의 특징은 삽입, 삭제, 탐색이 전부 O(lgN)에 처리할 수 있는 특징을 가진다. 이진 검색 트리는 사실 그냥 해시를 쓰면 되지않나 라는 생각이 들 수 있다. 왜냐하면 해시는 위 연산이 대부분 O(1)에 처리되기 때문이다. 그러나 이진 검색트리의 강력한 점은 모든 원소가 크기순으로 정렬되어 있다는 점이다. 만약 1,3,5,7,9에서 5보다 큰 최초의 원소가 뭘까를 고민할 때 해시에서는 이를 알 방법이 없지만, 이진 검색 트리는 O(lgN)으로 알 수 있기 때문이다.
삽입(Insert)
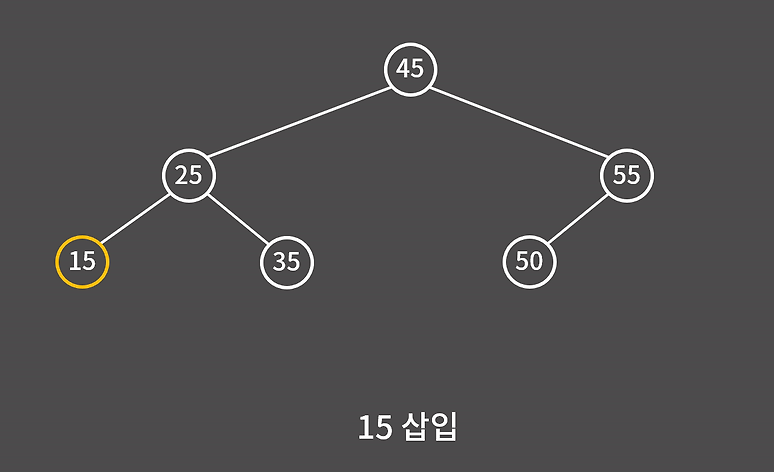
트리에 값을 삽입할 때는 비교를 통해 알맞은 위치를 찾아 내려가며 넣는다.
- 45를 먼저 넣으면 트리의 루트가 된다.
- 다음으로 25를 넣으면 45보다 작기 때문에 45의 왼쪽 자식이 된다.
- 그 다음 35를 넣으면 45보다 작고 25보다는 크므로, 25의 오른쪽 자식이 된다.
이러한 과정을 반복하면 아래 그림과 같은 트리가 완성된다.
탐색(Find)
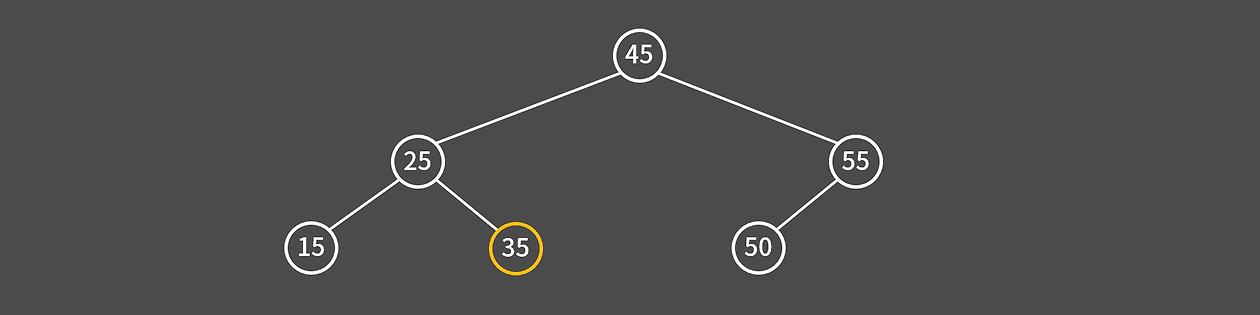
탐색은 루트에서 시작해서 조건에 따라 좌우로 내려가면서 원하는 값을 찾는다.
- 루트 45에서 시작 → 35는 더 작으므로 왼쪽으로 이동
- 25에 도착 → 35는 더 크므로 오른쪽으로 이동
- 35에 도달 → 탐색 성공
삭제(Erase)
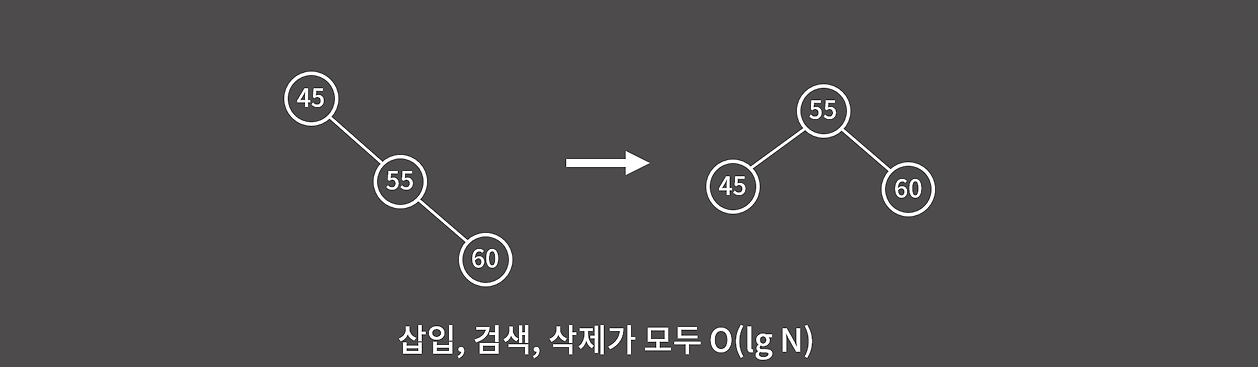
삭제는 이진 검색 트리에서 가장 까다로운 연산이다.
단순히 노드를 없애면 연결 구조가 무너지기 때문에, 트리의 특성을 유지하면서 삭제해야 한다.
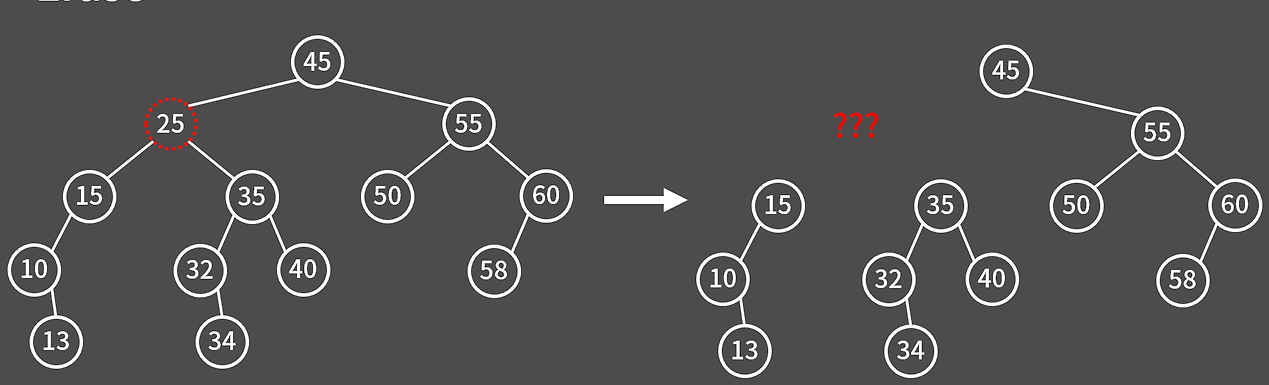
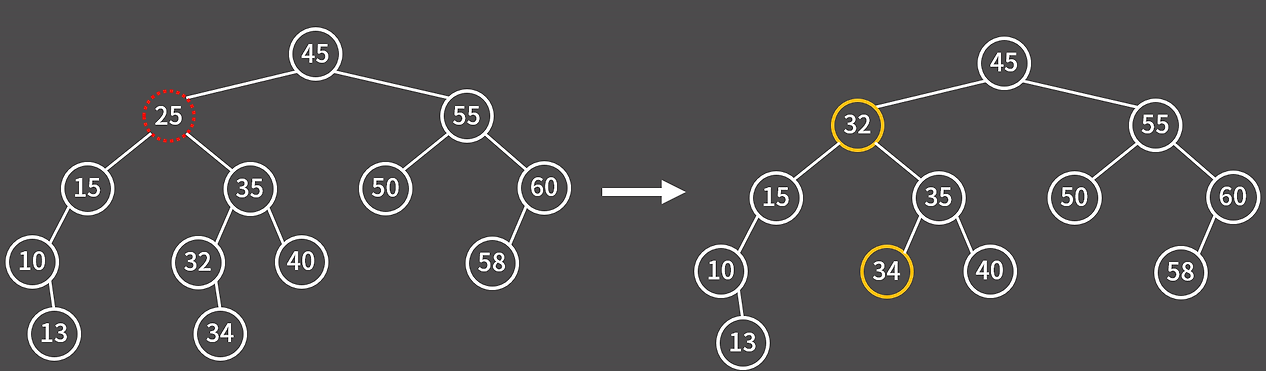
이때는 25의 자리에 트리 규칙을 만족하는 다른 노드를 올려야 한다. 25의 오른쪽 서브트리에서 가장 작은 값을 선택해서 올리는 것이 일반적인 방식이다.
- 25의 오른쪽 자식은 35
- 35의 왼쪽 자식은 32, 그 왼쪽 자식은 34
- 따라서 25 자리에 32를 올리고, 32 자리는 다시 34로 대체하면 된다.
여기서 바로 15를 올려도 문제는 없다.
반대로 자식이 0개(단말 노드)거나 1개인 경우는 훨씬 단순하다. 단말 노드는 그냥 삭제하고, 자식이 1개인 경우는 자식 노드를 위로 올리면 된다.
자가 균형 트리
이진 검색 트리를 위해선 높이에 따라 시간 복잡도가 정해지는데 만약 1,2,4,8처럼 배수로 증가하여 트리가 형성되는 경우 노드가 편향되어 높이가 O(N)에 가까워져서 복잡도가 O(lgN)이 아닌 O(N)으로 형성될 것이다.
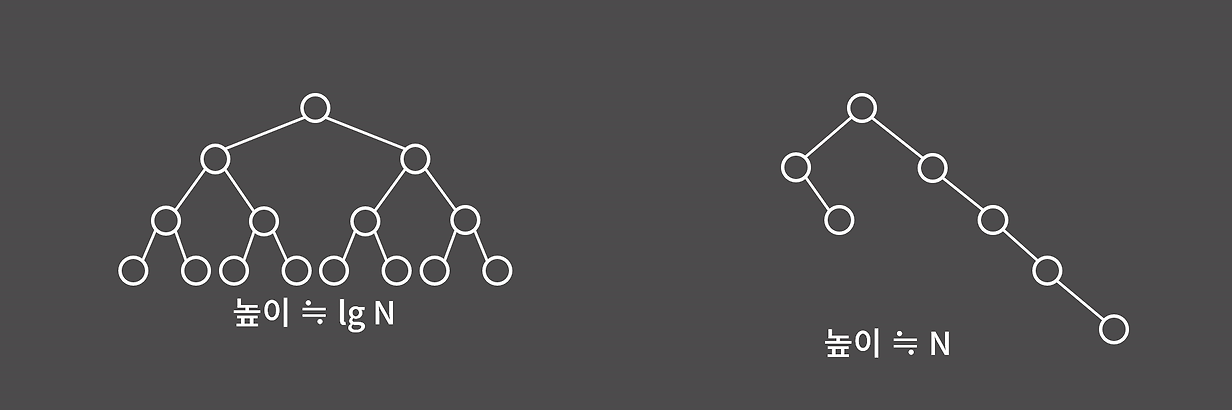
이러한 경우엔 이진 검색 트리의 이점을 사용할 수 없기 이런 편향되는 경우를 해결하기 위해 자가 균형 트리가 존재한다. 자가 균형 트리는 만약 1,2,4,8 이 존재하여 저렇게 높이가 깊어지는 경우 중간을 꺽어서 강제로 균형을 맞추는 정도만 이해하면 된다.
자식이 0개 1개 2개 등 케이스에 따라 구현이 많이 복잡하기 때문에 위 설명 정도로만 가볍게 이해하면 된다.
STL
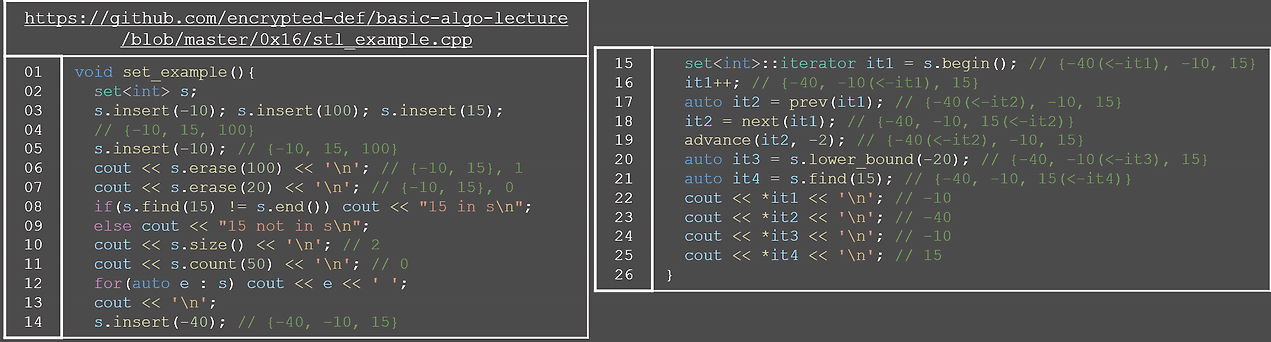
해당 이진 검색 트리는 코드로 구현하기 매우 까다롭고 어렵기 때문에 다행히 STL에 있는 기능을 사용하면 된다. 지난번 unordered_set과 같이 해시를 사용하였는데
그냥 set, map, multiset 등 앞에 unordered가 안 붙은 것이 바로 이진 검색 트리이다. 원소가 삽입될때마다 알아서 정렬되기 때문에 삽입 삭제 탐색 전부 O(lgN)의 시간 복잡도를 가진다.
가장 중요한 이진이 붙었기 때문에 이분 탐색에서 사용했던 lower_bound 같은 함수가 내장되어 있어 바로 사용이 가능하다.
위 내용을 정리하면 다음과 같다.
- set, map, multiset 등은 내부적으로 이진 검색 트리 기반으로 동작한다.
- 앞에 unordered_가 붙으면 해시 기반이고, 안 붙으면 이진 검색 트리 기반이다.
- 이진 검색 트리 기반 자료구조는 삽입, 삭제, 탐색이 전부 O(logN)이며, 자동 정렬된 상태로 유지된다.
- 또한 lower_bound, upper_bound 같은 함수도 사용할 수 있다.
마무리
이진 검색 트리는 이론적으로도 실무적으로도 꽤 중요한 자료구조로 알고 있다.
직접 구현은 어렵지만 STL 등을 통해 쉽게 사용할 수 있고 알고리즘 문제나 코딩 테스트에서 자주 등장하는 개념이기도 하다.
기본 원리를 이해하고 다양한 문제를 풀어보며 활용법을 익히다 보면 더 자연스럽게 받아들일 수 있을 것이다.
Reference
[실전 알고리즘] 0x16강 이진 검색 트리 - BaaaaaaaarkingDog