1. 문제
한국도로공사는 고속도로의 유비쿼터스화를 위해 고속도로 위에 N개의 센서를 설치하였다. 문제는 이 센서들이 수집한 자료들을 모으고 분석할 몇 개의 집중국을 세우는 일인데, 예산상의 문제로, 고속도로 위에 최대 K개의 집중국을 세울 수 있다고 한다.
각 집중국은 센서의 수신 가능 영역을 조절할 수 있다. 집중국의 수신 가능 영역은 고속도로 상에서 연결된 구간으로 나타나게 된다. N개의 센서가 적어도 하나의 집중국과는 통신이 가능해야 하며, 집중국의 유지비 문제로 인해 각 집중국의 수신 가능 영역의 길이의 합을 최소화해야 한다.
편의를 위해 고속도로는 평면상의 직선이라고 가정하고, 센서들은 이 직선 위의 한 기점인 원점으로부터의 정수 거리의 위치에 놓여 있다고 하자. 따라서, 각 센서의 좌표는 정수 하나로 표현된다. 이 상황에서 각 집중국의 수신 가능영역의 거리의 합의 최솟값을 구하는 프로그램을 작성하시오. 단, 집중국의 수신 가능영역의 길이는 0 이상이며 모든 센서의 좌표가 다를 필요는 없다.
2. 입력
첫째 줄에 센서의 개수 N(1 ≤ N ≤ 10,000), 둘째 줄에 집중국의 개수 K(1 ≤ K ≤ 1000)가 주어진다. 셋째 줄에는 N개의 센서의 좌표가 한 개의 정수로 N개 주어진다. 각 좌표 사이에는 빈 칸이 하나 있으며, 좌표의 절댓값은 1,000,000 이하이다.
3. 출력
첫째 줄에 문제에서 설명한 최대 K개의 집중국의 수신 가능 영역의 길이의 합의 최솟값을 출력한다.
4. 테스트 케이스
예제 입력 1
6
2
1 6 9 3 6 7
예제 출력 1
5
예제 입력 2
10
5
20 3 14 6 7 8 18 10 12 15
예제 출력 2
7
5. 풀이
처음에 문제 이해가 되지 않아 여러 번 읽고 나서야 문제를 이해하게 되었다.
고속도로에는 N개의 센서가 있으며 K개의 집중국을 설치해야 한다. 단, 집중국의 수신 가능 영역의 거리의 합이 최소가 되어야 한다.
-> 고속도로의 N개의 센서를 K개의 구역으로 나누고, 해당 구역의 거리의 합이 최소가 되어야 한다.
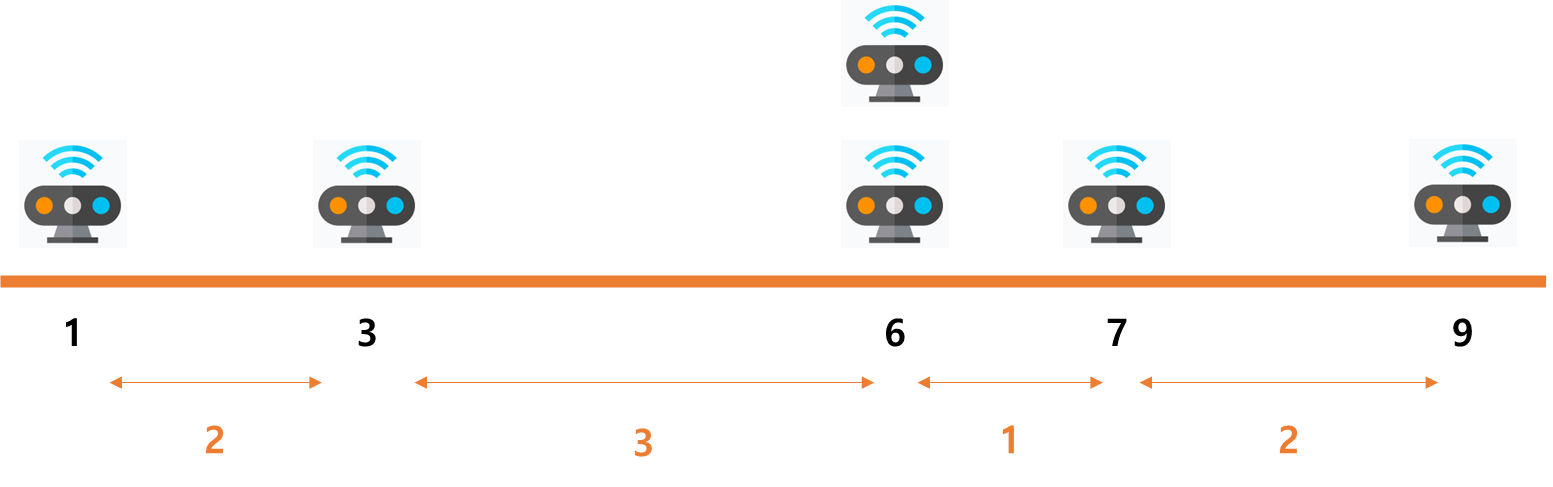
위의 그림은 [예제 입력 1번]을 나타낸 것이다.
화살표의 숫자는 센서를 정렬한 후 인접한 센서 사이의 거리를 나타낸 것이다.
여기서 센서를 2개의 구역으로 나누어 해당 구역의 거리의 합이 최소가 되려면 3인 부분을 제외해야 한다.
따라서, 가장 긴 거리를 하나씩 지워나간 후 남은 거리의 합을 구하면 최소가 된다는 것을 알 수 있다. 즉, k-1 개의 거리를 지우고 나머지의 합을 구하면 된다.
가장 긴 거리를 k-1개 지우기 위해, 거리를 정렬하여 (n-1) - (k-1) 까지의 합을 더하면 된다.
import java.io.*;
import java.util.*;
public class boj_2212 {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer stk;
StringBuilder sb = new StringBuilder();
int n = Integer.parseInt(br.readLine()); // 센서 개수
int k = Integer.parseInt(br.readLine()); // 집중국 개수
int[] sensor = new int[n];
stk = new StringTokenizer(br.readLine());
for (int i = 0; i < n; i++) {
sensor[i] = Integer.parseInt(stk.nextToken());
}
Arrays.sort(sensor); // 1. 센서 정렬
int[] diff = new int[n - 1]; // 거리 배열
// 2. 센서 간의 거리 구해서 배열에 저장
for (int i = 0; i < n - 1; i++) {
diff[i] = sensor[i + 1] - sensor[i];
}
Arrays.sort(diff); // 3. 거리 정렬
// 4. n-k까지의 합 출력
int sum = 0;
for (int i = 0; i < n - k; i++)
sum += diff[i];
// 5. 정답 출력
sb.append(sum);
System.out.println(sb);
}
}