Tree

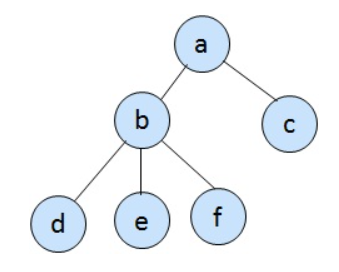
1개 이상의 유한한 개수의 노드 집합
루트 노드와 0개 이상의 하위 나무 구조들의 집합(부모-자식)으로 이루어짐

Node : 정보를 저장하는 공간
Edge : 관계를 나타내는 선

Node 는 배열에 들어가는 값(혹은 그와 유사한 구현체)을 생각하면 되고, Edge 를 통해 형성된 형태를 특정한 기준에 따라 탐색해 나가는 과정이 대부분의 Tree 알고리즘 형태이다.

Tree 의 추가적인 정보

size : 자신을 포함한 모든 자식 노드의 개수
leaf node : 자식이 없는 node, 단말노드라고도 불린다
level : 트리의 특정 깊이를 가지는 노드의 집합 root 부터 level 1~
depth : 루트 노드에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선 수의 최솟값
height : 루트 노드에서 가장 깊숙히 있는 노드의 깊이

Binary Tree

자식이 최대 2개인 Node 집합을 말하며, Tree 알고리즘에서 대표적으로 쓰이는 Tree 구조

알고리즘에서 자주 쓰이는 이유는 자식을 단순한 연산(왼쪽 자식은 nodeNum x 2, 오른쪽 자식은 nodeNum x 2 +1)으로 접근 가능하기 때문이다.

perfect binary tree : 모든 노드의 자식이 2개인 tree

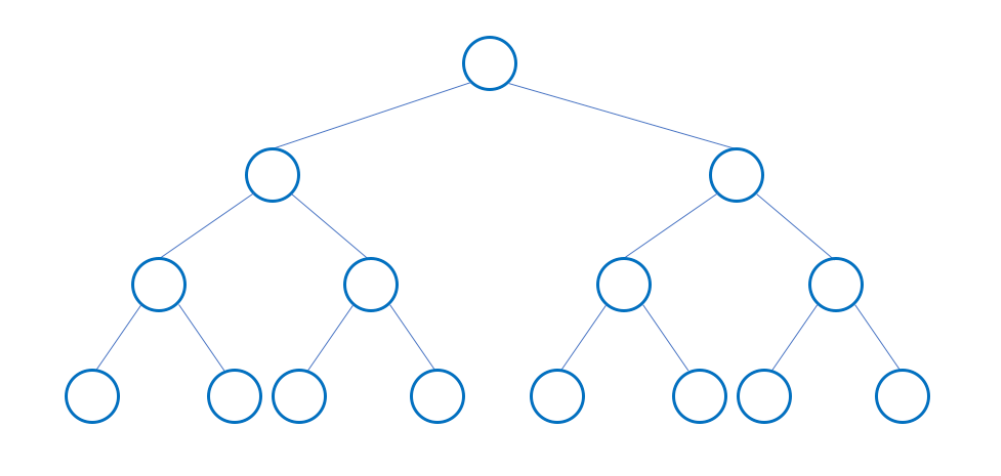
complete binary tree : 가장 높은 레벨을 제외하고 모든 레벨의 노드가 가득 차 있어야함(가장 높은 레벨은 왼쪽 자식부터 채워짐)

-Heap Tree 에 사용되는 구조

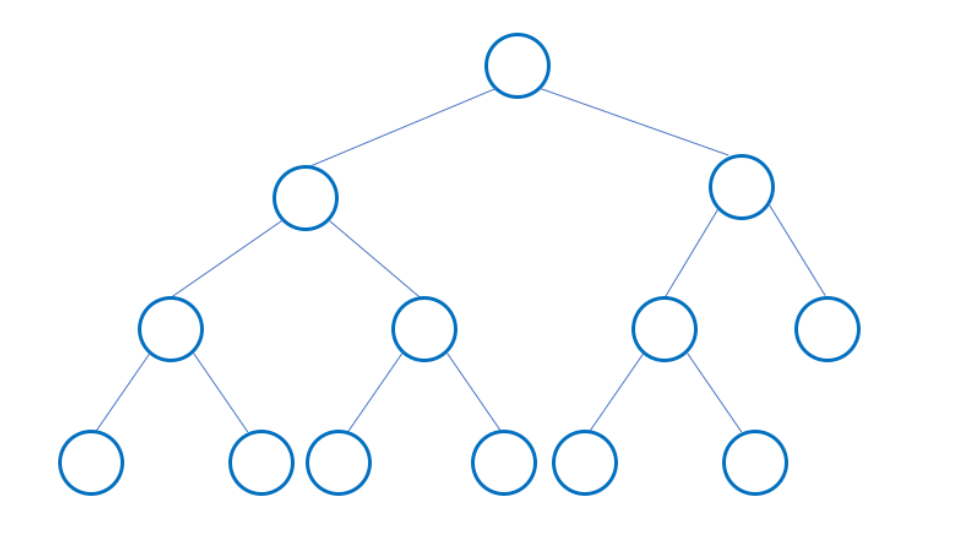
full binary tree : 모든 노드의 자식이 0개 이거나 2개인 tree

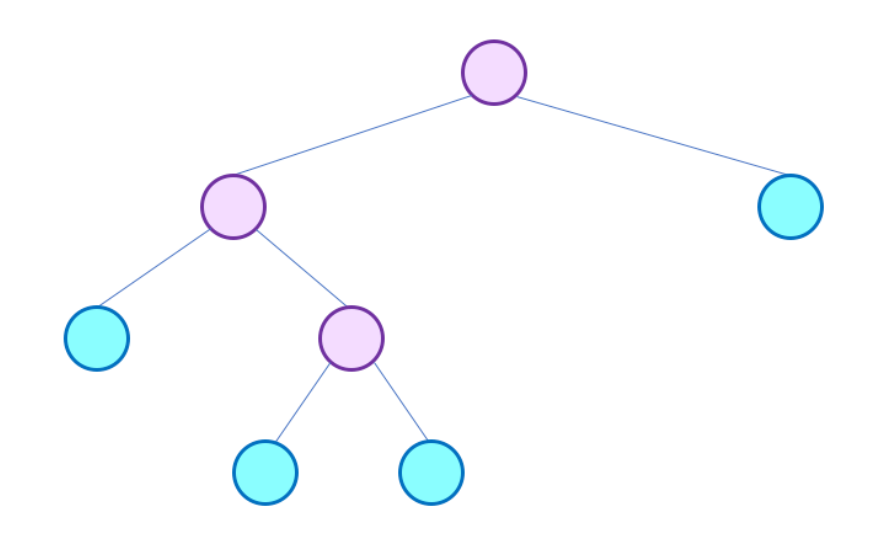
탐색법

Root node 에서 트리를 탐색해 나가는 방법에도 여러가지 규칙이 있다.
그 중 가장 기본이 되는 전위, 중위, 후위 순회에 대해서 알아보자

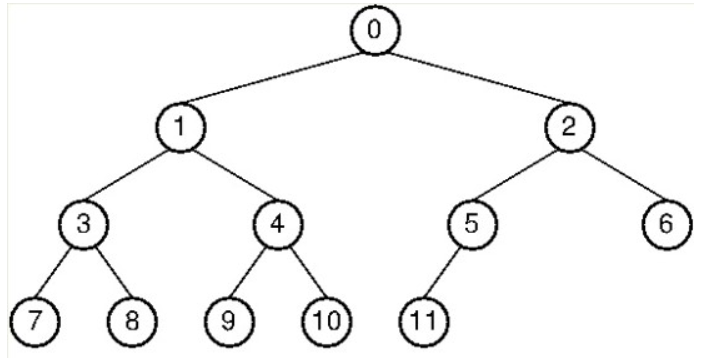
전위순회 : ROOT부터 무조건 왼쪽 자식부터 탐색
0-1-3-7-8-4-9-10-2-5-11-6
중위순회 : 왼쪽 하위 자식을 다 돌고 ROOT탐색
7-3-8-1-9-4-10-0-11-5-2-6
후위순회 : 자식 다 돌고 ROOT탐색
7-8-3-9-10-4-1-11-5-6-2-0