
Heap 은 알고리즘 문제에도 가끔 활용되는 힙한 자료구조인데요..
Swift 에는 기본으로 제공하는 Heap 자료구조가 없기 때문에, Swift 로 Heap 을 구현하는 방법 을 알아보겠습니다.
우선 Heap 이 뭔지 알아봅시당
🏗 자료구조 Heap
정의
- 최대 값 또는 최소 값을 빠르게 찾기 위한 자료구조
최대 힙 (Max Heap) : 부모 노드가 자식 노드보다 큰 값을 가지는 힙
최소 힙 (Min Heap) : 부모 노드가 자식 노드보다 작은 값을 가지는 힙
- 완전이진트리 (Complete Binary Tree) 를 기반
완전 이진 트리에서, 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 모든 노드는 가능한 한 가장 왼쪽에 있다. ... 완전 이진 트리는 배열을 사용해 효율적으로 표현 가능하다. - 📚 위키피디아 이진트리
- 반정렬 상태 (느슨한 정렬 상태) 유지
부모 (parent) - 자식 (child) 노드 간 대소 관계가 있으나,
형제 (sibling) 노드 간 대소 관계 없음
배열
Heap 은 완전이진트리 를 기반으로 합니다.
완전이진트리 는 마지막 계층을 제외한 모든 계층이 채워져있고, 마지막 계층은 왼쪽부터 채워져있습니다.
→ 사이사이 빈 공간이 없고 선형으로 표현하기 쉽기 때문에 배열로 구현하기 편합니다.
또한 배열을 사용할 경우 인덱스를 통해 부모, 자식 노드 사이 접근이 용이합니다. (아래 그림의 숫자는 인덱스입니다.)
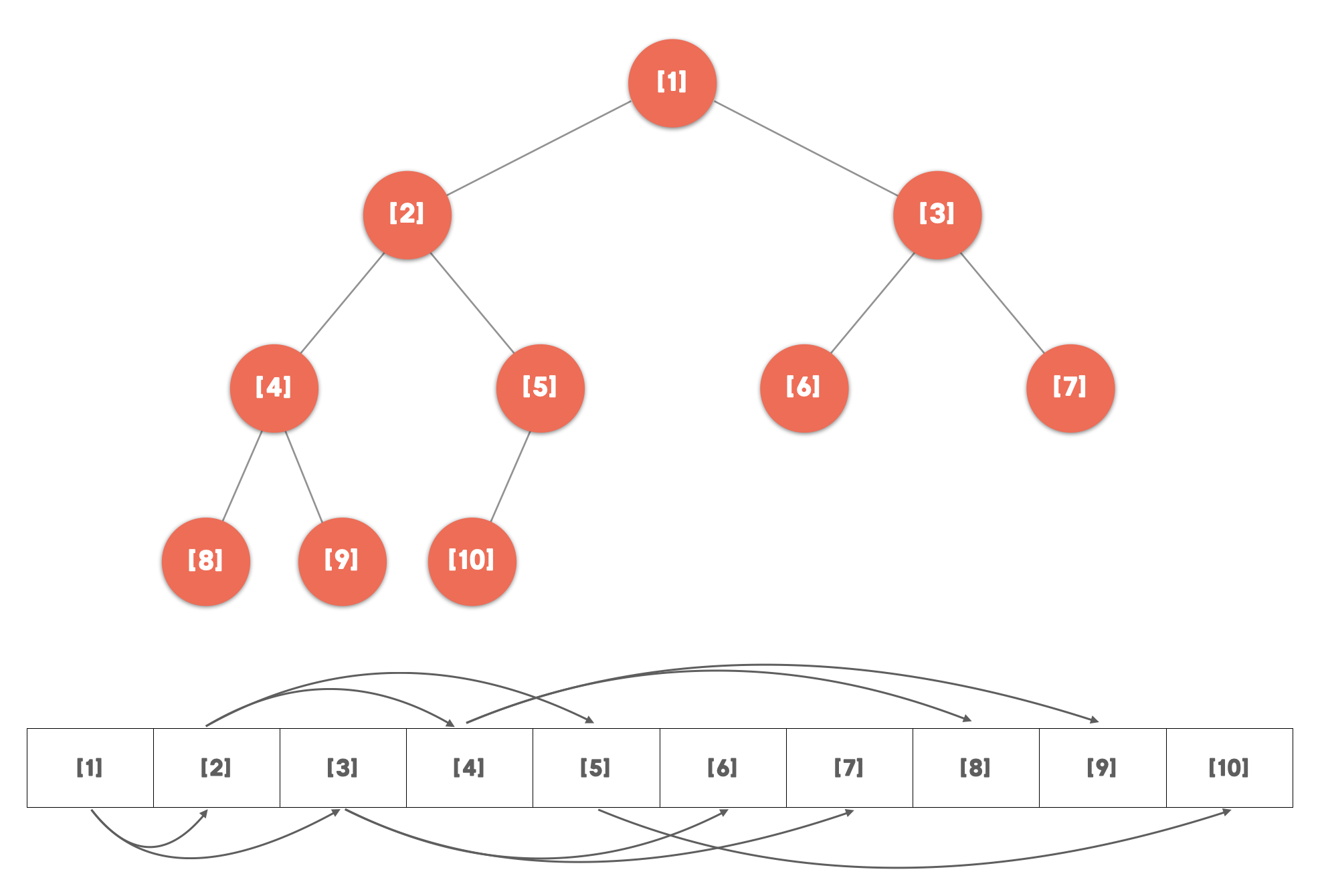
인덱스가 1 부터 시작하는 이유는 구현의 편의성 때문입니다!
- 자식 노드의 인덱스
- 왼쪽 자식 :index * 2
- 오른쪽 자식 :index * 2 + 1
- 부모 노드의 인덱스
-index / 2
🧑💻구현
이번 포스팅에서는 부모 노드의 값이 자식 노드들의 값보다 큰 최대 힙 (Max Heap) 을 구현해보겠습니다.
Protocol
protocol Heap {
var array : [Int] { get set }
mutating func insert(_ data : Int)
mutating func pop() -> Int?
mutating func sort()
func sorted() -> [Int]
static func heapify(_ array: inout [Int])
}
extension Heap {
func display() {
if array.count == 1 { print("Empty!") }
else { print(array[1..<array.endIndex]) }
}
func getParentIndex(_ index : Int) -> Int { index / 2 }
func getLeftChildIndex(_ index : Int) -> Int { index * 2 }
func getRightChildIndex(_ index : Int) -> Int { index * 2 + 1 }
}최소 힙 (MinHeap) 구현의 확장성 을 위해 protocol 과 protocol extension 을 활용했고, 포스팅의 가독성을 위해 Generic 타입을 받는 대신 정수형 데이터만 사용했습니다.
📌 힙의 종류에 따라 구현을 다르게 할 함수 → protocol
array: 힙을 저장할 배열
insert: 힙에 데이터를 넣기 위한 함수pop: 힙에서 데이터를 꺼내기 위한 함수
sort,sorted: 힙소트 를 위한 함수heapify: Heapify 를 위한 함수 (Heap 자료구조로 만들기 위한 함수)
💥 mutating 키워드
구조체 (struct) 로 Heap 을 구현 할 예정이기 때문에, 값 타입 (Value type) 의 내부 변수 수정 이 필요한
insert함수와pop함수는mutating키워드 사용을 하게 되었습니다!
📌 힙의 종류에 상관없이 사용할 함수 → protocol extension
display: 힙 출력 함수getParentIndex,getLeftChildIndex,getRightChildIndex: 부모, 자식 노드의 인덱스를 구하기 위한 함수
Enum
enum Child {
case none
case left
case both
static func type(_ index : Int, size : Int) -> Self {
if size < index * 2 + 1 { return .none }
else if size == index * 2 + 1 { return .left }
else { return .both }
}
}자식 노드의 타입을 표현하기 위한 enum 입니다.
static func type(_ index : Int, size : Int) 으로 해당 인덱스의 노드가 자식노드를 둘 다 갖는지, 자식노드 하나만 갖는지, 자식 노드가 없는지 를 판별합니다.
위의 트리 이미지와 함께 보시면 이해하기 쉽습니다 :)
Struct
struct MaxHeap : Heap {
var array = Array<Int>()
var maxValue : Int? {
if array.count == 1 { return nil }
else { return array[1] }
}
init() { array.append(Int.max) }
...최대 힙 자료구조 를 struct 를 사용하여 생성했습니다.
0번째 인덱스에 Int 최대 값을 넣어두었습니다.
그 이유는.. 삽입 (insert) 의 구현에 있어서 코드의 간결함을 높일 수 있기 때문입니다!
Insert
힙에서 데이터의 삽입은 배열의 가장 끝에 데이터를 삽입하고 반복적으로 부모 노드와 비교하고 필요시 교환하여 힙의 구조를 유지합니다.
작업의 방향은 아래에서 위 방향 ⬆️ 입니다!
최대 힙의 경우에 삽입한 데이터가 부모 노드보다 크면 부모 노드와 자리를 바꾸는 작업을 반복합니다.

mutating func insert(_ data : Int) {
var currentIndex = array.count
array.append(data)
while array[getParentIndex(currentIndex)] < array[currentIndex] {
array.swapAt(getParentIndex(currentIndex), currentIndex)
currentIndex = getParentIndex(currentIndex)
}
}while loop 를 돌면서, 부모 노드의 값보다 크면 교환 하는 작업을 반복 합니다.
📌 0번째 노드에
Int.max값을 넣음으로써 0번째 인덱스에 대한 예외 처리를 하지 않을 수 있습니다.(
Int.max보다 큰 값이 들어올 일이 없기 때문입니당)
Pop
힙에서의 데이터 꺼내기란 최대 값 또는 최소 값을 꺼내는 것 입니다.
구현 방식은 첫 번째 노드 (최대 값 또는 최소 값) 를 제거하고 배열의 마지막 데이터를 첫번째로 옮겨 첫번째 노드부터 자식 노드와 반복 비교하며 힙의 구조를 유지 합니다.
작업의 방향은 위에서 아래 방향 ⬇️ 입니다!
최대 힙의 경우에 첫번째 노드에 있던 최대 값을 꺼내고, 배열의 마지막 데이터를 첫 번째 노드로 옮긴 후 자식 노드와 비교했을 때 자식 노드 중 큰 값 보다 작으면 교환하는 작업을 반복합니다.

mutating func pop() -> Int? {
if array.count == 1 { return nil }
else if array.count == 2 { return array.removeLast() }
var currentIndex = 1
let returnValue = array[currentIndex]
array[currentIndex] = array.removeLast()
while true {
switch Child.type(currentIndex, size : array.count) {
case .both :
let greaterChildIndex = array[currentIndex * 2] > array[currentIndex * 2 + 1] ? currentIndex * 2 : currentIndex * 2 + 1
if array[greaterChildIndex] > array[currentIndex] { array.swapAt(greaterChildIndex, currentIndex) }
currentIndex = greaterChildIndex
case .left :
if array[getLeftChildIndex(currentIndex)] > array[currentIndex] { array.swapAt(getLeftChildIndex(currentIndex), currentIndex) }
return returnValue
case .none :
return returnValue
}
}
}returnValue 에 반환할 최대 값을 저장해두고,
array.removeLast() 를 사용해서 마지막 노드를 꺼내어 첫 번째 노드로 저장합니다.
while loop 를 돌면서, 자식 노드 중 큰 값보다 작으면 교환 하는 작업을 반복 합니다.
이때, 자식 노드의 개수에 따라 동작이 다름으로 구분하여 코드를 작성합니다.
enum Child에 구현한type함수를 통해 자식 노드의 개수를 판별하고
- 자식 노드가 2개일 경우 : 두 자식 노드 중 큰 값을 가진 노드와 비교하여 자식 노드 보다 작은 값을 가진다면 교환
- 자식 노드가 1개일 경우 : 비교하여 자식 노드 보다 작은 값을 가진다면 교환하고 종료
- 자식 노드가 없을 경우 : 종료
💥 Heapify
Heapify 란 Heap 자료구조로 변환하는 것을 의미합니다.
단순히 insert() 를 반복하면 되지 않을까 라고 생각할 수 있지만, 이는 메모리를 2배로 사용하는 방법입니다.
대신 부모 - 자식 노드 간의 관계를 비교하여 교환하는 방식으로 구현할 수 있습니다.
- 0번째 인덱스에
Int.max삽입- (데이터의 개수 (
array.count- 1) / 2) ~ 1 인덱스를 가진 노드에 대해서 작업 📌
(마지막 레벨의 노드 (Leaf 노드) 에 대해서는 작업을 하지 않겠다는 의미 입니다! - 이해가 되지 않는다면, 공비가 2인 등비수열을 떠올려보세요!)pop과 비슷하게 인덱스에 해당 하는 노드에서 자식 노드와 비교하여 교환하는 작업을 반복- 작업의 방향은 위에서 아래 방향 ⬇️!
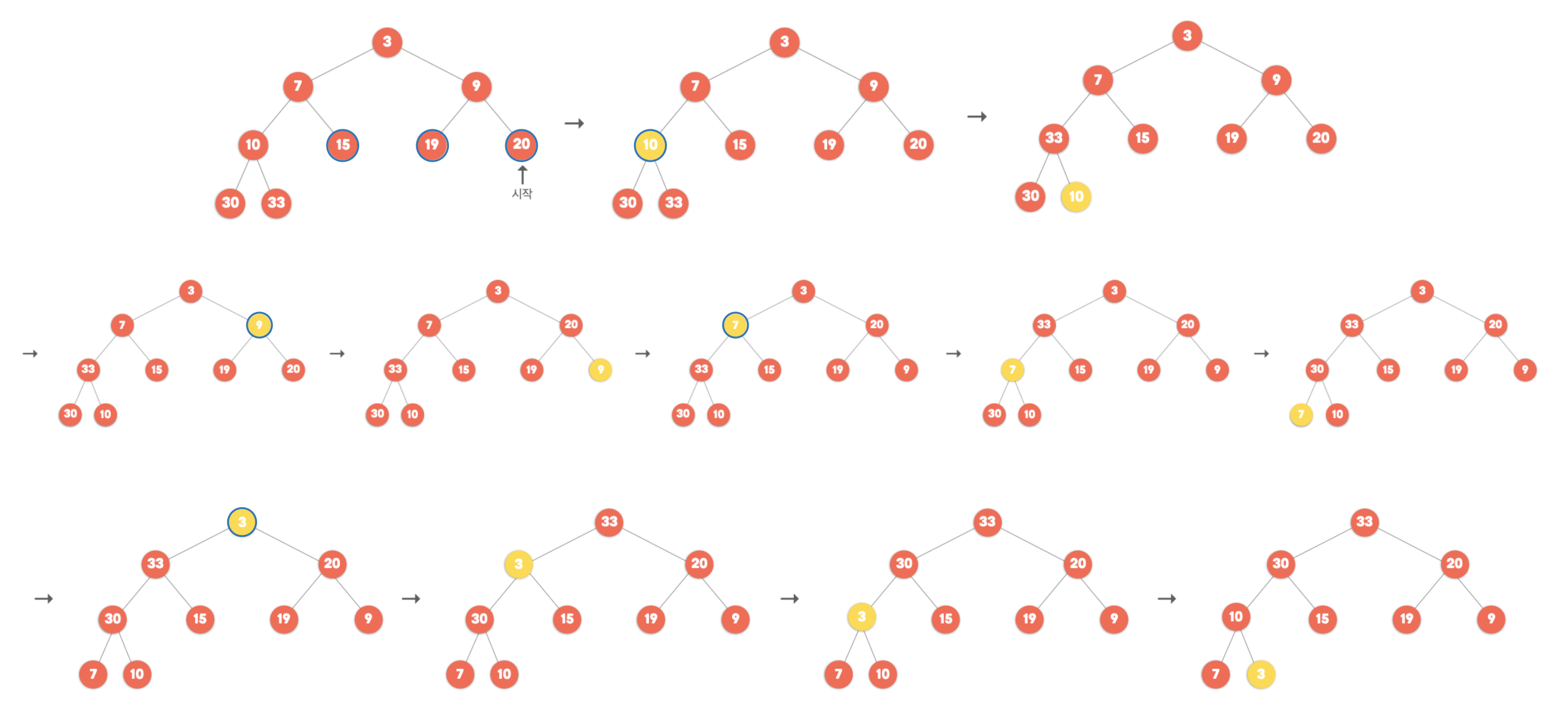
static func heapify(_ array: inout [Int]) {
array.insert(Int.max, at: 0)
for index in (1...(array.count - 1) / 2).reversed() {
var currentIndex = index
loop : while true {
switch Child.type(currentIndex, size : array.count) {
case .both :
let greaterChildIndex = array[currentIndex * 2] > array[currentIndex * 2 + 1] ? currentIndex * 2 : currentIndex * 2 + 1
if array[greaterChildIndex] > array[currentIndex] { array.swapAt(greaterChildIndex, currentIndex) }
currentIndex = greaterChildIndex
case .left :
let leftChildIndex = currentIndex * 2
if array[leftChildIndex] > array[currentIndex] { array.swapAt(leftChildIndex, currentIndex) }
break loop
case .none :
break loop
}
}
}
}⌛️ 정렬
힙 정렬은 힙 자료구조를 활용한 정렬 방법 입니다.
첫번째 인덱스의 값 (최대 값 또는 최소 값) 을 배열의 마지막 값과 교환하고, 배열의 크기를 줄여가며 힙의 구조를 유지하는 작업을 반복하여 정렬된 배열을 얻을 수 있습니다.
최대 힙에서는
- 최대 값을 가진 첫번째 인덱스의 값을 배열의 마지막 인덱스 값과 교환
- 배열의 크기를 줄인 후, 첫번째 인덱스 부터 힙 자료구조를 유지하기 위한 작업 반복 ⬇️
- 위 작업을 반복하면 최종적으로 오름차순으로 저장!
mutating func sort() {
if array.count == 1 { return }
else if array.count == 2 { return }
var currentIndex = 1
for i in 1..<array.count {
currentIndex = 1
array.swapAt(currentIndex, array.count - i)
loop : while true {
switch Child.type(currentIndex, size : array.count - i) {
case .both :
let greaterChildIndex = array[currentIndex * 2] > array[currentIndex * 2 + 1] ? currentIndex * 2 : currentIndex * 2 + 1
if array[greaterChildIndex] > array[currentIndex] { array.swapAt(greaterChildIndex, currentIndex) }
currentIndex = greaterChildIndex
case .left :
if array[getLeftChildIndex(currentIndex)] > array[currentIndex] { array.swapAt(getLeftChildIndex(currentIndex), currentIndex) }
break loop
case .none :
break loop
}
}
}
}
func sorted() -> [Int] {
var array = array
if array.count == 1 { return [] }
else if array.count == 2 { return array }
var currentIndex = 1
for i in 1..<array.count {
currentIndex = 1
array.swapAt(currentIndex, array.count - i)
loop : while true {
switch Child.type(currentIndex, size : array.count - i) {
case .both :
let greaterChildIndex = array[currentIndex * 2] > array[currentIndex * 2 + 1] ? currentIndex * 2 : currentIndex * 2 + 1
if array[greaterChildIndex] > array[currentIndex] { array.swapAt(greaterChildIndex, currentIndex) }
currentIndex = greaterChildIndex
case .left :
let leftChildIndex = currentIndex * 2
if array[leftChildIndex] > array[currentIndex] { array.swapAt(leftChildIndex, currentIndex) }
break loop
case .none :
break loop
}
}
}
return Array(array[1..<array.endIndex])
}Array 의 sort() 와 sorted() 처럼 두 가지 정렬함수를 구현하였습니다.
작동 원리는 같으나,
mutating sort(): 추가 메모리를 사용하지 않지만 원본 힙 구조를 변경함
sorted() -> [Int]: 추가 메모리를 사용하되 원본 힙 구조를 손상시키지 않고 새로운 정렬된 배열 반환
📌 Time Complexity
- 최대 값 또는 최소 값 구하기 →
O(1)
힙 배열의 첫번째 인덱스 데이터를 반환하면 됩니다.var maxValue : Int? { if array.count == 1 { return nil } else { return array[1] } }
- 데이터 삽입 →
O(logN)
최악의 경우 트리의 높이 만큼 반복합니다.
- 데이터 삭제 →
O(logN)
최악의 경우 트리의 높이 만큼 반복합니다.
- Heapify →
O(NlogN)
(N / 2) * logN으로O(NlogN)의 시간 복잡도를 가집니다.
- 정렬 →
O(NlogN)
배열의 원소 개수만큼 1번 인덱스부터 아래로 비교와 교환을 반복하기 때문에O(NlogN)의 시간 복잡도를 가집니다.
👍 마무리
오늘은 Heap 자료구조에 대해 알아보고 Swift 로 최대 힙 (MaxHeap) 을 구현해보았습니다.
코드와 샘플 데이터가 궁금하신 분은 ParkGyurim99/Algorithm/Heap 를 참조해주세요!
틀린 정보 또는 궁금한 점이 있다면 댓글 부탁드립니다! 읽어주셔서 감사합니다‼️

글이 굉장히 Heap 하시네요 ㅎㅎㅎ