O(nlogn)의 시간복잡도
O(nlogn)의 시간복잡도를 가진 정렬은 퀵정렬, 힙정렬, 합병정렬 3가지가 존재한다.
모두 다 트리의 개념이 들어간다는 공통점을 가지고 있다.
1.1 퀵정렬 - 원리
-
리스트 안에 있는 한 요소를 선택한다. 이렇게 고른 원소를 피벗(pivot) 이라고 한다.
-
피벗을 기준으로 피벗보다 작은 요소들은 모두 피벗의 왼쪽으로 옮겨지고 피벗보다 큰 요소들은 모두 피벗의 오른쪽으로 옮겨진다. (피벗을 중심으로 왼쪽: 피벗보다 작은 요소들, 오른쪽: 피벗보다 큰 요소들)
-
피벗을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬한다.
- 분할된 부분 리스트에 대하여 순환 호출 을 이용하여 정렬을 반복한다.
- 부분 리스트에서도 다시 피벗을 정하고 피벗을 기준으로 2개의 부분 리스트로 나누는 과정을 반복한다.
-
부분 리스트들이 더 이상 분할이 불가능할 때까지 반복한다.
- 리스트의 크기가 0이나 1이 될 때까지 반복한다.
public static void main(String[] args) {
int[] input = {13, 5, 11, 7, 23, 15};
quick_sort(input);
System.out.println(Arrays.toString(input));
}
public static void quick_sort(int[] s){
quick_sort(s, 0, s.length-1);
}
public static void quick_sort(int[] s, int start, int end){
// 배열을 2개로 나눴을때 오른쪽 파티션의 시작지점
int part2 = partition(s, start, end);
// 파티션을 나눴을때 왼쪽 파티션의 길이가 1이 아닐때
if(start < part2 - 1){
quick_sort(s, start, part2 - 1);
}
// 파티션을 나눴을때 오른쪽 파티션의 길이가 1이 아닐때
if(part2 < end){
quick_sort(s, part2, end);
}
}
public static int partition(int[] s, int start, int end){
int pivot = s[(start + end) / 2];
while(start<=end){
// 피벗을 중심으로 왼쪽으로는 작은 요소, 오른쪽으로는 큰 요소를 나누는 작업
while(s[start] < pivot) start++;
while(s[end] > pivot) end--;
if(start<=end){
swap(s, start, end);
start++;
end--;
}
}
return start;
}
public static void swap(int[] s, int start, int end){
int tmp = s[start];
s[start] = s[end];
s[end] = tmp;
}
// [5, 7, 11, 13, 15, 23]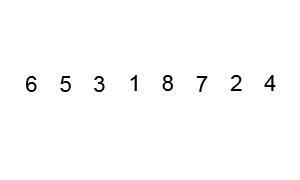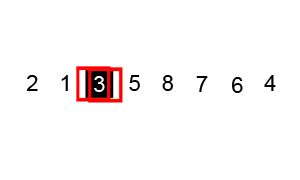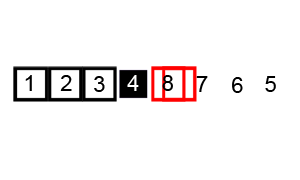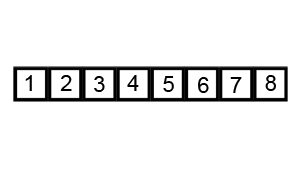
1.2 퀵정렬 - 장점
- 평균적으로 가장 빠른 속도를 보입니다.
- 시간 복잡도가 O(nlog₂n)를 가지는 다른 정렬 알고리즘과 비교했을 때도 가장 빠르다.
- 추가 메모리 공간을 필요로 하지 않는다.
- 퀵 정렬은 O(log n)만큼의 메모리를 필요로 한다.
1.3 퀵정렬 - 단점
- 최악의 경우, O(n^2)의 성능을 보이며, pivot을 어떻게 선택하느냐에 따라 성능이 달라집니다.
2.1 힙정렬 - 원리
- 정렬해야 할 n개의 요소들로 최대 힙(완전 이진 트리 형태)을 만든다.
- 내림차순을 기준으로 정렬
- 그 다음으로 한 번에 하나씩 요소를 힙에서 꺼내서 배열의 뒤부터 저장하면 된다.
- 삭제되는 요소들(최댓값부터 삭제)은 값이 감소되는 순서로 정렬되게 된다.

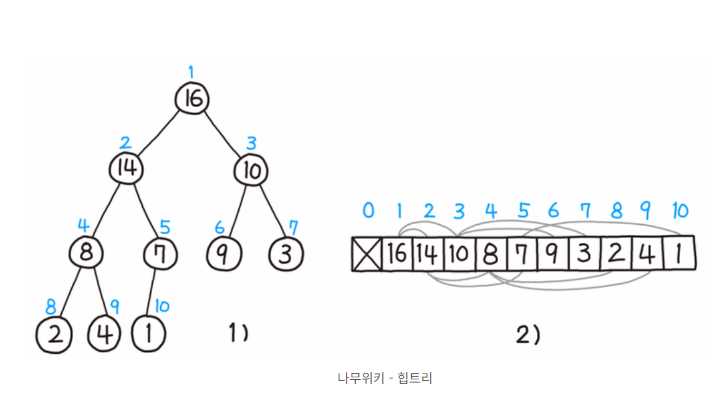
2-2 힙정렬 - 특징
-
최대힙 Max Heap : 부모 노드 값은 항상 자식 노드 값보다 크다 (=Root 노드 값이 가장 크다) - 기본적으로 최대힙의 특징을 가지고 있다.
-
최소힙 Min Heap : 자식 노드 값은 항상 부모 노드 값보다 크다 (=Root 노드 값이 가장 작다)
힙의 배열 저장은 위의 사진 2)를 참고해서 보면 쉽다.
부모는 Arr[ i ]
왼쪽 자식은 Arr[ 2i +1 ]
오른쪽 자식은 Arr[ 2i +2 ]
ex) 10은 Arr[3], 9는 Arr[6], 3은 Arr[7]
public static void main(String[] args) {
int[] input = {13, 5, 11, 7, 23, 15};
heapSort(input, input.length);
System.out.println(Arrays.toString(input));
}
static void heapSort(int[] arr, int n) {
//힙구조로 구성 (Build Max-heap)
heapify(arr, n);
//루트 제거하고 마지막 요소를 루트로 옮김 (Extract-Max)
for(int i=n-1; i>=0; i--) {
swap(arr, 0, i);
heapify(arr, i);
}
}
//Build Max-heap
static void heapify(int[] arr, int last) { //last변수는 가장 마지막 인덱스를 뜻함
for(int i=1; i<last; i++) {
int child = i;
while(child>0) {
int parent = (child - 1)/2;
if(arr[child] > arr[parent]) { //부모와 비교해서 자식이 클경우엔
swap(arr, child, parent); //swap
}
child = parent;
}
}
}
//배열의 요소 두개의 위치를 바꿈
static void swap(int[] arr, int idx1, int idx2) {
int tmp = arr[idx1];
arr[idx1]=arr[idx2]; //idx1 : idx1 -> idx2
arr[idx2]=tmp; //idx2 : idx2 -> idx1
}2.3 힙정렬 - 장점
- 최악의 경우에도 O(NlogN) 으로 유지가 된다.
- 힙의 특징상 부분 정렬을 할 때 효과가 좋다.
2.4 힙정렬 - 단점
- 일반적인 O(NlogN) 정렬 알고리즘에 비해 성능은 약간 떨어진다.
- 한 번 최대 힙을 만들면서 불안정 정렬 상태에서 최댓값만 갖고 정렬을 하기 때문에 안정정렬이 아니다.
3.1 합병정렬 - 원리
- 리스트의 길이가 0 또는 1이면 이미 정렬된 것으로 본다.
- 그렇지 않은 경우에는 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
- 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
- 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다.
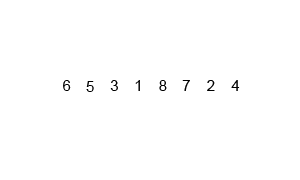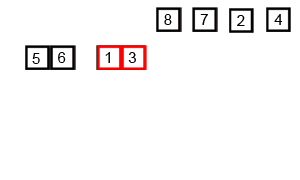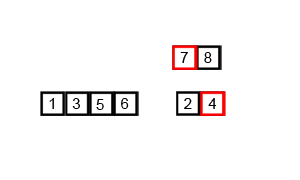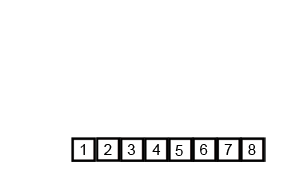
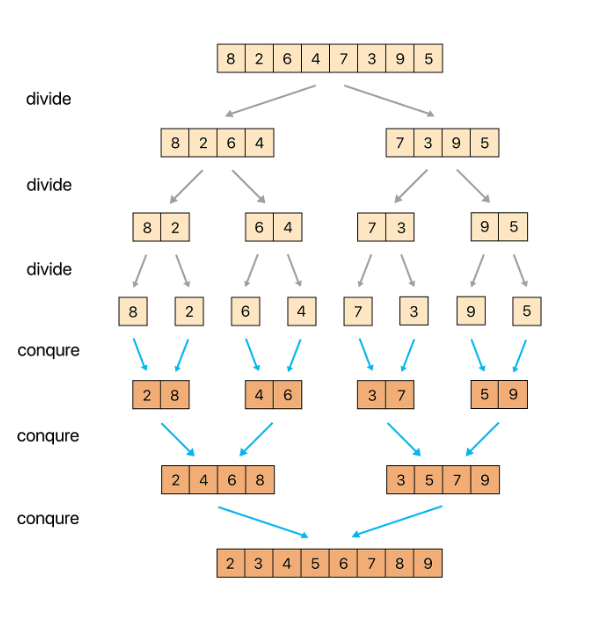
위 사진은 2,3번 작업을 진행하는 사진
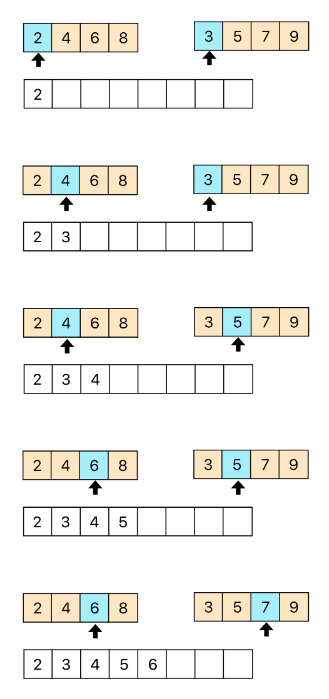
위 사진은 4번 작업을 진행하는 사진
private static int[] sorted; // 합치는 과정에서 정렬하여 원소를 담을 임시배열
public static void main(String[] args) {
int[] input = {13, 5, 11, 7, 23, 15};
merge_sort(input);
System.out.println(Arrays.toString(input));
}
public static void merge_sort(int[] a) {
sorted = new int[a.length];
merge_sort(a, 0, a.length - 1);
sorted = null;
}
// Top-Down 방식 구현
private static void merge_sort(int[] a, int left, int right) {
/*
* left==right 즉, 부분리스트가 1개의 원소만 갖고있는경우
* 더이상 쪼갤 수 없으므로 return한다.
*/
if(left == right) return;
int mid = (left + right) / 2; // 절반 위치
merge_sort(a, left, mid); // 절반 중 왼쪽 부분리스트(left ~ mid)
merge_sort(a, mid + 1, right); // 절반 중 오른쪽 부분리스트(mid+1 ~ right)
merge(a, left, mid, right); // 병합작업
}
/**
* 합칠 부분리스트는 a배열의 left ~ right 까지이다.
*
* @param a 정렬할 배열
* @param left 배열의 시작점
* @param mid 배열의 중간점
* @param right 배열의 끝 점
*/
private static void merge(int[] a, int left, int mid, int right) {
int l = left; // 왼쪽 부분리스트 시작점
int r = mid + 1; // 오른쪽 부분리스트의 시작점
int idx = left; // 채워넣을 배열의 인덱스
while(l <= mid && r <= right) {
/*
* 왼쪽 부분리스트 l번째 원소가 오른쪽 부분리스트 r번째 원소보다 작거나 같을 경우
* 왼쪽의 l번째 원소를 새 배열에 넣고 l과 idx를 1 증가시킨다.
*/
if(a[l] <= a[r]) {
sorted[idx] = a[l];
idx++;
l++;
}
/*
* 오른쪽 부분리스트 r번째 원소가 왼쪽 부분리스트 l번째 원소보다 작거나 같을 경우
* 오른쪽의 r번째 원소를 새 배열에 넣고 r과 idx를 1 증가시킨다.
*/
else {
sorted[idx] = a[r];
idx++;
r++;
}
}
/*
* 왼쪽 부분리스트가 먼저 모두 새 배열에 채워졌을 경우 (l > mid)
* = 오른쪽 부분리스트 원소가 아직 남아있을 경우
* 오른쪽 부분리스트의 나머지 원소들을 새 배열에 채워준다.
*/
if(l > mid) {
while(r <= right) {
sorted[idx] = a[r];
idx++;
r++;
}
}
/*
* 오른쪽 부분리스트가 먼저 모두 새 배열에 채워졌을 경우 (r > right)
* = 왼쪽 부분리스트 원소가 아직 남아있을 경우
* 왼쪽 부분리스트의 나머지 원소들을 새 배열에 채워준다.
*/
else {
while(l <= mid) {
sorted[idx] = a[l];
idx++;
l++;
}
}
/*
* 정렬된 새 배열을 기존의 배열에 복사하여 옮겨준다.
*/
for(int i = left; i <= right; i++) {
a[i] = sorted[i];
}
}3.2 합병정렬 - 장점
- 항상 두 부분리스트로 쪼개어 들어가기 때문에 최악의 경우에도 O(NlogN) 으로 유지가 된다.
- 안정적인 정렬로 같은 값의 원소들은 정렬 과정에서 상대적인 순서가 변경되지 않는다.
3.3 합병정렬 - 단점
- 정렬과정에서 추가적인 보조 배열 공간을 사용하기 때문에 메모리 사용량이 많다.
- 레코드들의 크기가 큰 경우에는 보조 배열에서 원본배열로 복사하는 과정이 많으므로 매우 큰 시간적 낭비를 초래한다.