💡 목표

• 자신없던 최소신장트리와 크루스칼 알고리즘, 프림 알고리즘을 정리하면서 공부하고자 합니다.

📌 최소 신장트리

✅ 그래프에서 최소 비용 문제

1. 모든 정점을 연결하는 간선들의 가중치의 합이 최소가 되는 트리
2. 두 정점 사이의 최소 비용의 경로 찾기

✅ 신장트리

- n개의 정점으로 이루어진 무향 그래프에서 n개의 정점과 n-1개의 간선으로 이루어진 트리

✅ 최소 신장 트리 (Minimum Spanning Tree)

- 무향 가중치 그래프(undirected weighted graph)에서 신장 트리를 구성하는 간선들의 가중치의 합이 최소인 신장 트리

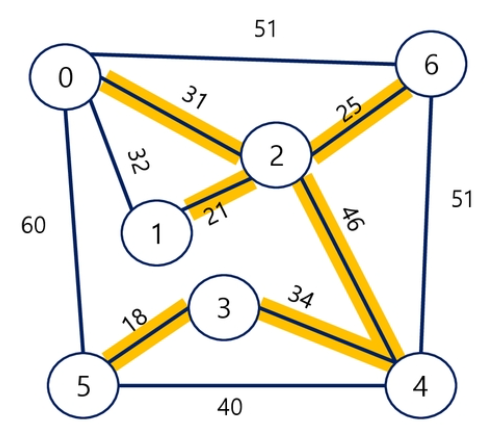
KRUSKAL 알고리즘(간선 선택)

1. 모든 간선을 가중치에 따라 ((오름차순 정렬))
2. 가중치가 낮은 간선부터 선택하면서 트리를 증가시킴
   • 사이클이 존재한다면? 다음으로 가중치 낮은 간선 선택
3. n-1개의 간선이 선택될 때까지 2번을 반복

흐름을 봅시다 🎨

1. 오름차순으로 간선을 정렬합니다.

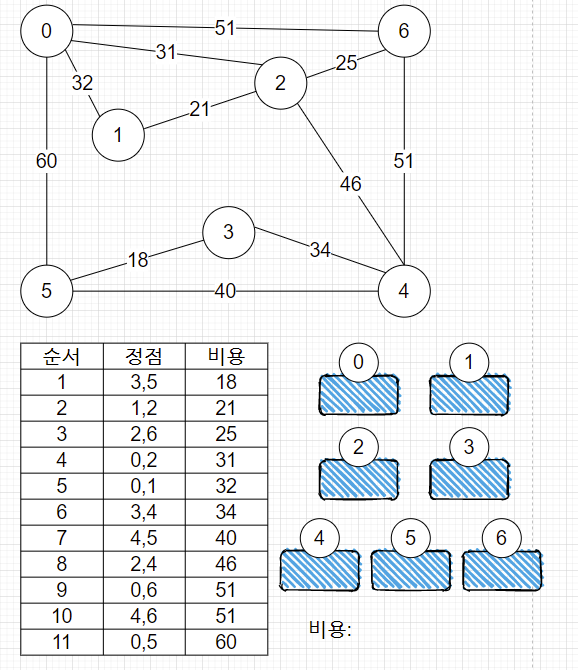
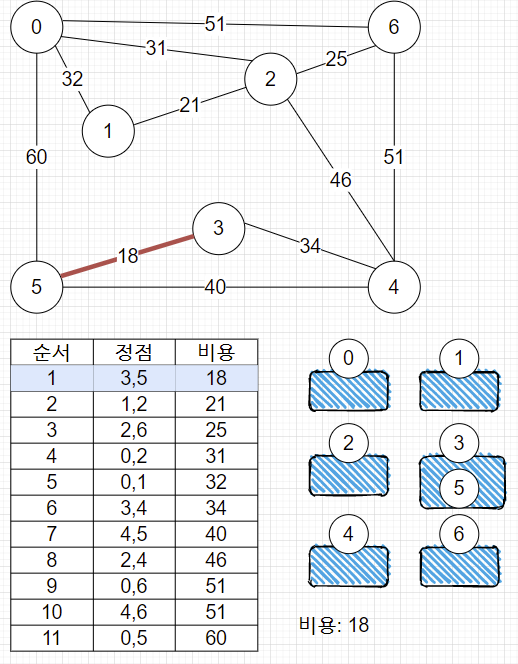
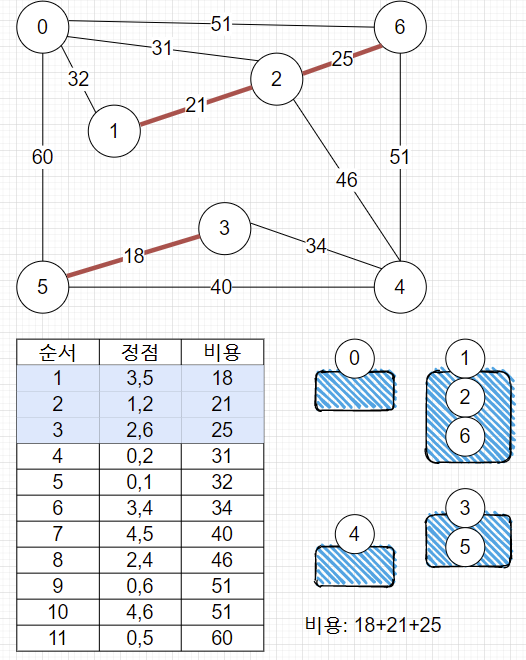
2. 비용이 제일 작은 3,5 간선 선택

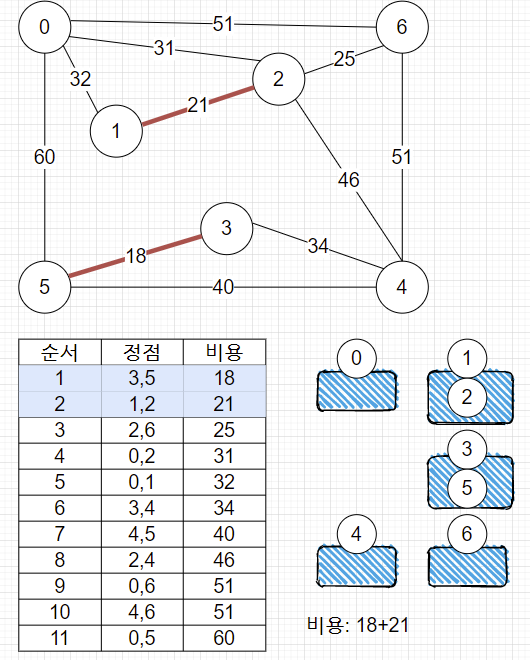
3. 그다음 1,2 간선 선택

4. 계속 진행

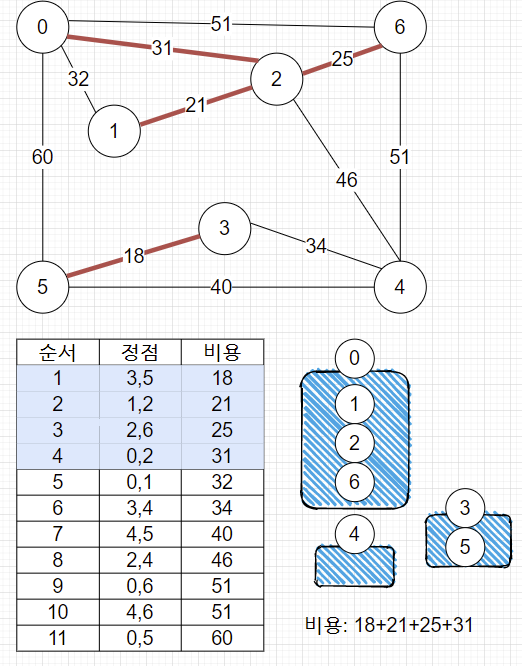
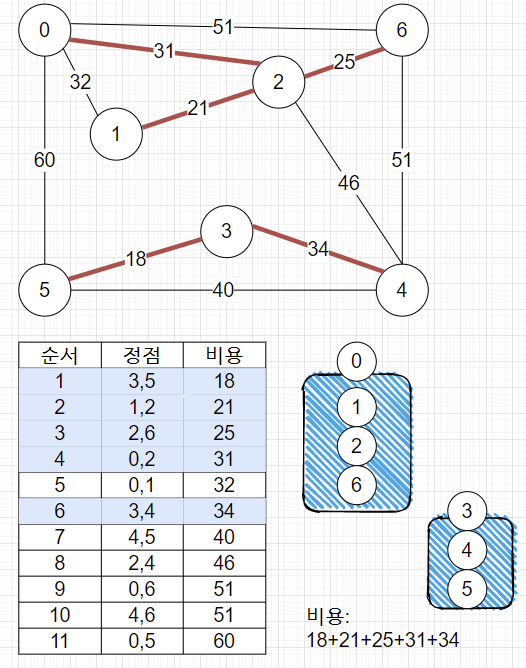
5. 사이클이 존재한다면? 다음으로 넘어갑니다.

• 0, 1 이미 같은 집합이므로 union 불가
  

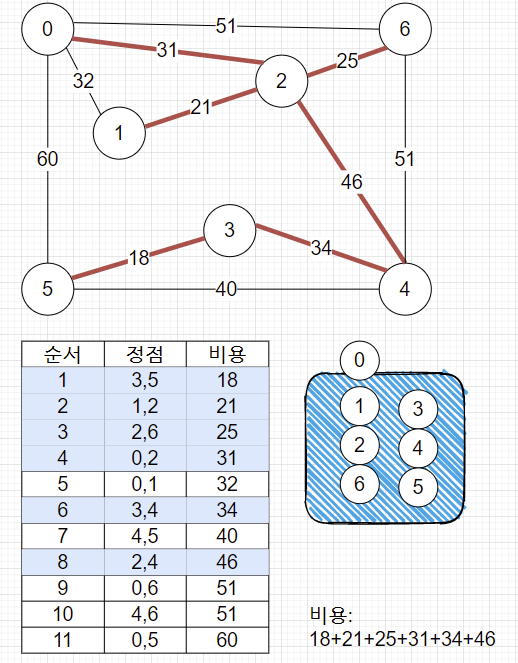
6. N-1개의 간선 선택 완료

Java로 구현

import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

public class MSTKruskalTest {

	// 간선 정보 저장하는 객체 -> 정렬되어야함
	static class Edge implements Comparable<Edge> {
		int start, end, weight;

		public Edge(int start, int end, int weight) {
			this.start = start;
			this.end = end;
			this.weight = weight;
		}

		@Override
		public int compareTo(Edge o) {
			return Integer.compare(weight, o.weight); // 오름차순
		}
	}

	static int[] parents; // 부모 원소를 관리 (트리처럼 사용) // 사이클이 발생하는지 여부 체크
	static int V, E; // Vertex, Edge // 정점, 간선
	static Edge[] edgeList; // 간선들 저장하는 배열 -> 정렬되어야함

	private static void make() {
		parents = new int[V];
		// 모든 원소를 자신을 대표자로 만듦
		for (int i = 0; i < V; i++) {
			parents[i] = i;
		}
	}

	// a가 속한 집합의 대표자 찾기
	private static int find(int a) {
		if (a == parents[a])
			return a; // 자신이 대표자
		return parents[a] = find(parents[a]); // 자신이 속한 집합의 대표자를 자신의 부모로 : path compression
	}

	// 두 원소를 하나의 집합으로 합치기(대표자를 이용해서 합침)
	private static boolean union(int a, int b) {
		int aRoot = find(a);
		int bRoot = find(b);
		if (aRoot == bRoot)
			return false; // 이미 같은 집합으로 합치지 않음

		parents[bRoot] = aRoot;
		return true;
	}

	public static void main(String[] args) throws Exception {
		System.setIn(new FileInputStream("res/kruskal_input.txt"));
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine(), " ");

		V = Integer.parseInt(st.nextToken());
		E = Integer.parseInt(st.nextToken());

		// 간선 리스트 작성
		edgeList = new Edge[E];

		for (int i = 0; i < E; i++) {
			st = new StringTokenizer(br.readLine(), " ");
			int start = Integer.parseInt(st.nextToken());
			int end = Integer.parseInt(st.nextToken());
			int weight = Integer.parseInt(st.nextToken());
			edgeList[i] = new Edge(start, end, weight);
		}

		Arrays.sort(edgeList); // 오름차순 정렬

		make(); // 모든 정점을 각각의 집합으로 만들고 출발

		// 간선 하나씩 시도하며 트리 만들어 감.
		int cnt = 0, result = 0; // cnt: 연결 간선 수 result: 최소비용들의 합
		for (Edge e : edgeList) {
			if (union(e.start, e.end)) {  // 시작정점 - 끝정점을 연결 시도
				// 서로 다른 집합이었다가 합쳐지는 게 가능한 경우. start, end는 이제 같은 집합이 됨
				result += e.weight; // 비용누적
				if (++cnt == V - 1) // 연결 간선수가 정점수-1이면 다 연결한 것임
					break; // 신장트리 완성
			}
		}

		System.out.println(result);
	}

}

PRIM 알고리즘(정점 선택)

1. 임의의 정점 하나 선택해서 시작
2. 선택한 정점과 인접하는 정점들 중의 최소 비용의 간선이 존재하는 정점을 선택
3. N개의 모든 정점이 선택될 때 까지 1번, 2번 과정을 반복

서로소인 2개의 집합 정보를 유지

1. 트리 정점들 - MST를 만들기 위해 선택된 정점들
2. 비트리 정점들 - 선택되지 않은 정점들

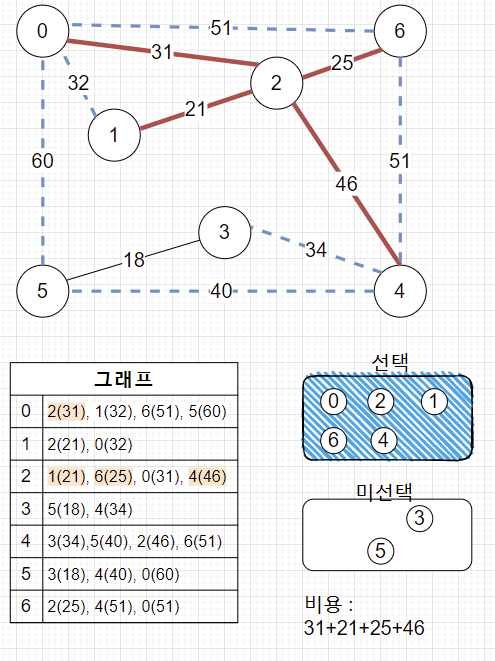
흐름을 봅시다 🎨

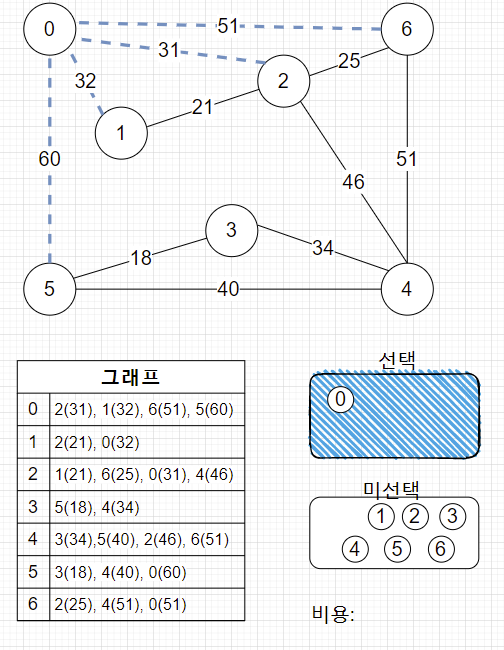
1. 임의의 정점 0을 선택, 0에서 제일 적은 비용인 2와 연결합니다.

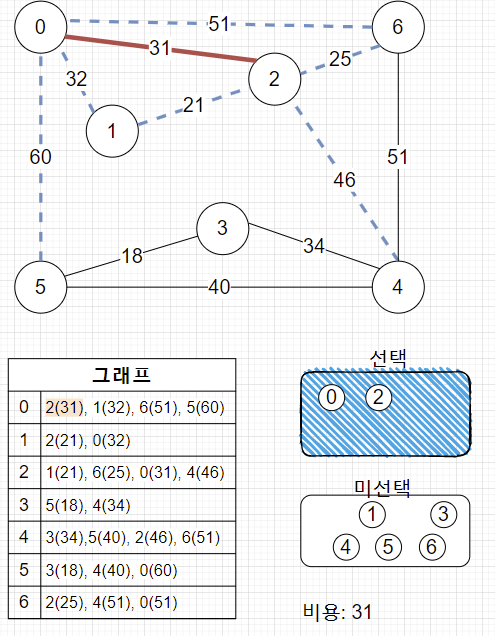
2. 0, 2번 정점에서 최소비용 간선 선택합니다. (제일 작은 21 간선)

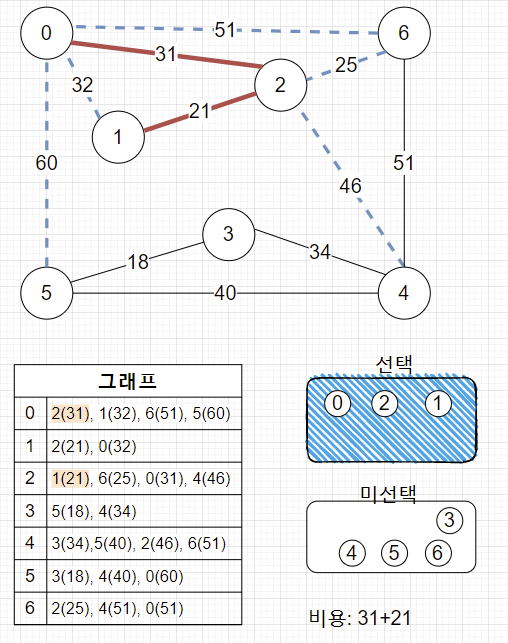
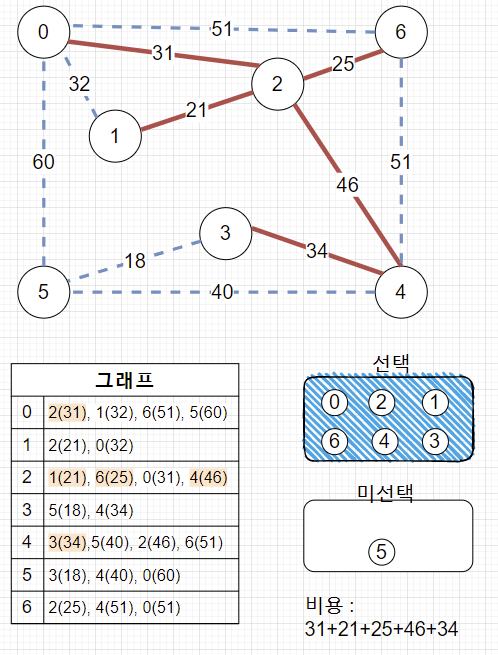
3. 계속 진행 (32 간선 선택 x)

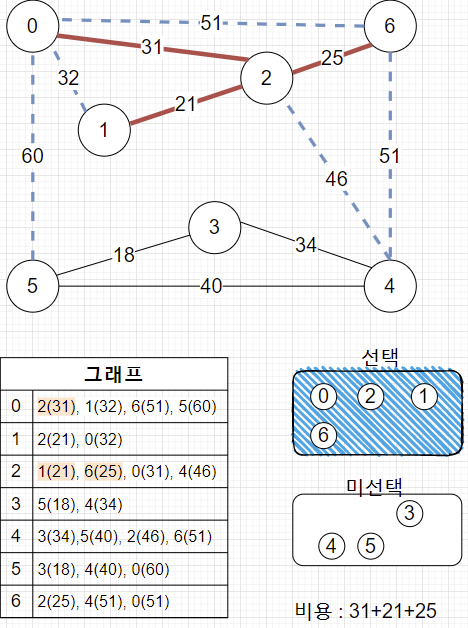
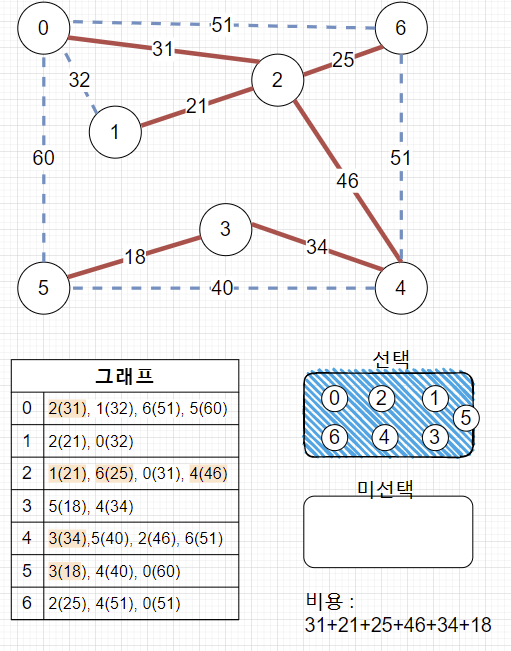
4. N개의 정점이 다 선택되었으면 끝.

Java로 구현

import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

// 임의의 정점 (시작점)을 시작으로 최소비용의 간선을 선택하고 -> 최소비용 정점이 결정 됨 -> mst에 포함
public class MSTPrimTest {

	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

		int N = Integer.parseInt(br.readLine());
		int[][] adjMatrix = new int[N][N];
		boolean[] visited = new boolean[N]; // 해당 정점의 방문 여부체크. 해당 정점이 mst에 포함되었는지 여부 체크
		int[] minEdge = new int[N]; // 각 정점별 다른 정점과의 연결 간선 비용 중 최소값.
		// 한 정점과 연결된 다른 간선들의 비용 중 최소값

		StringTokenizer st = null;
		for (int i = 0; i < N; i++) {
			st = new StringTokenizer(br.readLine(), " ");
			for (int j = 0; j < N; j++) {
				// 정점 i -> j로 가는 간선이 존재하고 그 때 가중치가 adjMatrix[i][j]
				adjMatrix[i][j] = Integer.parseInt(st.nextToken());
			}
			minEdge[i] = Integer.MAX_VALUE;
		}

		int result = 0; // 최소신장트리 비용
		minEdge[0] = 0; // 임의의 시작점 0의 간선비용을 0으로 세팅

		for (int i = 0; i < N; i++) { // 모든 정점 수만큼 반복
			// 1. 신장트리에 포함되지 않은 정점 중 최소간선비용의 정점 찾기
			int minCost = Integer.MAX_VALUE;
			int minVertex = -1; // 최소간선비용의 정점번호

			// 1. 현재 모든 정점 중에서 가장 작은 간선 비용을 갖는 정점을 찾고 그 때의 비용은 얼마인지 찾음
			for (int j = 0; j < N; j++) {
				// !visited[j]: 정점 i가 mst에 포함이 안됐고
				if (!visited[j] && minCost > minEdge[j]) {
					minCost = minEdge[j]; // 최소 간선 비용
					minVertex = j; // 최소 간선 비용을 가지는 정점의 번호
				}
			}

			visited[minVertex] = true; // 신장트리에 포함시킴
			result += minCost; // 간선비용 누적

			// 2. 선택된 정점 기준으로 신장트리에 연결되지 않은 타 정점과의 간선 비용 최소로 업데이트
			// 새로 찾은 정점(minVertex)과 연결된 다른 정점들과의 최소 간선 비용을 업데이트
			for (int j = 0; j < N; j++) {

				// adjMatrix[minVertex][j] != 0 : 0이 아니라는 것은 인접해야 한다는 뜻
				if (!visited[j] && adjMatrix[minVertex][j] != 0 && minEdge[j] > adjMatrix[minVertex][j]) {
					minEdge[j] = adjMatrix[minVertex][j];
				}

			}
		}

		System.out.println(result);
	}

}