Printf

Bigmountain·2020년 10월 27일
42Seoulft_printf
0

42Seoul

목록 보기
2/7

Subject

문제 이해하기

  • 변환하는 서식문자는 cspdiuxX% 로 구현한다.
  • It will manage any combination of the following flags: ’-0.*’ and minimum field width with all conversions 이건 뭔소리지 ?
    • 포맷 형식에서 주어진 -0.* 4개의 문자로 번역해라.
    • - , 0은 flags를 의미한다. (밑에서 정리)
    • *은 정수를 입력받아서 처리하는 문자이다.
    • .은 정밀도를 나타내기위한 기호이다.

Bonus

  • 서식문자 nfge도 번역
  • 길이도 번역
  • flags에서 '#' ' ' '+'도 번역

Step1 : 가변인자 이해하기

참조

참조 1
참조 2

가변인자란?

  • C언어 함수 중, 매개변수의 개수가 정해지지 않은 함수가 존재할 수 있다.
  • 매번 함수에 들어가는 인수(argument)의 개수가 변하는 것을 가변 인자(가변 인수, variable argument)라고 한다.
  • 함수에서 가변 인자를 정의할 때는 고정 매개변수가 한 개 이상 있어야 하며, 고정 매개변수 뒤에 ...을 붙여 매개변수의 개수가 정해지지 않았다는 표시를 해준다. (...뒤에는 다른 매개변수를 지정할 수 없다.)
    • 고정 매개변수가 필요한 이유는 시작 위치를 알아야하기 때문이다. (아래 va_start참조)
      반환값 자료형 함수이름(자료형 고정매개변수, ...)
      {
         ...
      }

va_list

  • 가변 인수들을 저장할 수 있는 타입이다.
  • va_list타입에 저장된 인수들에 접근하기 위해서는 stdarg에 정의된 매크로를 사용한다.

va_start

void	va_start(va_list ap, last);
  • 가변 인수에 순차적으로 접근할 수 있도록, 시작 주소를 설정한다.
  • 인자로 va_list의 인수턴스와 마지막 위치의 고정인수를 전달한다.
    • 마지막 위치의 고정 인수란 아래와 같은 가변인수를 사용하는 함수가있을 때, args2에 해당한다.
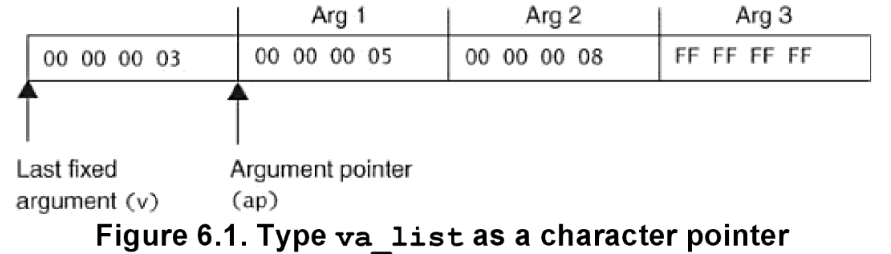
  • va_start 함수로 가변인수의 초기 주소값을 할당할 때, 아래와 같이 ap가 ...의 첫번 째 위치를 가르키게 만든다. (고로, 마지막 위치의 고정인수를 넘겨줘야 시작위치를 구분할 수 있다.)

va_start TEST

  • va_start할 때, 가변인자가 없으면 null값이 초기화 되나??? => No 없어도 주소는 할당 됨.
      void va_test(const char *str, ...) {
          va_list ap;
          printf("input str is : [%s]\n", str);
          va_start(ap, str);
          printf("ap address : [%p]\n", ap);
      }
      
      int main(int argc, const char *argv[]) {
          va_test("TEST");
          va_test("TOAST", 1, 2);
      }

va_arg

type	va_arg(va_list ap, type);
  • 가변 인자 메모리공간에서, 전달한 자료형의 크기만큼 값을 가져온다.
  • 값을 가져온 후, 포인터의 주소를 자료형 크기만큼 뒤로 옮겨서 다음 값을 가져올 수 있도록 한다.

va_end

void	va_end(va_list ap);
  • va_list의 포인터주소가 가르키는 값을 null로 초기화 한다.

va_copy

void	va_copy(va_list dest, va_list src);
  • src에 저장된 가변 파라메터를 dest로 복사한다.

가변인자 사용예시

      void printfNumbers(int args, int args2, ...)
      {
          va_list ap;

          va_start(ap, args2);
          for (int i = 0; i ＜ args; i++){
              int num = va_arg(ap, int);
              printf("%d ", num);
          }
          va_end(ap);    
          printf("\n");
      }

Step2 : printf 구조 이해하기

참조

참조 1
참조 2
참조 3
참조 4

printf 함수란?

  • 표준 출력(stdout)에 일련의 데이터들을 형식 문자열(format)에 지정되어 있는 형태로 출력한다.
  • 형식 문자열에는 형식 태그(format tag)라 불리는 것이 추가적으로 들어갈 수 있는데, 이에 대응하는 인자를 형식 태그가 지정한 형태로 치환되어 출력된다.
  • 따라서 형식 문자열 다음으로 오는 인자의 개수는 반드시 형식 문자열 속 태그의 개수 이상이어야 한다.
  • 형식 태그
%[플래그(flag)][폭(width)][.정밀도(precision)][길이(length)]서식 문자(specifier)

서식문자란 ?

  • 서식 문자(specifier)란 대응하는 인자를 어떠한 형태로 표현할지 결정하는 역할을 한다.
서식 문자설명예시
c문자'a'
d, i부호 있는 10진 정수
u부호 없는 10진 정수
e지수 표기법으로 출력, e문자 사용3.9265e + 2
E지수 표기법으로 출력, E문자 사용3.9265E + 2
f십진법 부동 소수점 수
g%f와 %e중에서 짧은 것을 사용 (소문자)
G%F와 %E중에서 짧은 것을 사용 (대문자)
o부호 없는 8진수 정수
s문자열
x부호 없는 16진 정수(소문자)1000(16) => 3e8
X부호 없는 16진 정수(대문자)1000(16) => 3E8
p포인터 주소
n아무것도 출력하지 않는다.
but 부호 있는 int형 포인터를 함께전달해야 한다.
전달 된 포인터에 출력 된 문자열의 갯수가 저장된다.		int num 1;
printf("123%n6789\n", &num1); // 123456789
printf("num : %d\n", num1); // 3
printf("12345%n6789\n", &num1); // 123456789
printf("num : %d\n", num1); // 5
printf("1%n6789\n", &num1); // 16789
printf("num : %d\n", num1); // 1
%%를 출력한다printf("%%\n"); // %

플래그(flag)

  • 출력 형식에 대해 추가적인 option(?)을 부여할 수 있다.
  • 플래그는 여러개를 동시에 사용할 수 있다.
    • width 에서 *로 인자를 음수로 받은 경우 -부호는 flag로 인식된다.
    • 0은 #, -, ' '와 함께 쓰일 수 있다.
    • -와 0이 함께 쓰이면, 0은 무시된다.
    // +, ' '가 같이 쓰이면 '+'가 우선시 된다.
    printf("[% 010d]\n", 123); //[ 000000123]
    printf("[%+ 010d]\n", 123); //[+000000123]
    printf("[% +010d]\n", 123); //[+000000123]
기호설명
-왼쪽 정렬하여 출력한다.
+양수(+), 음수(-)의 부호를 출력한다.
' ' (space)양수는 '+' 부호를 붙이지않고 공백으(' ')로 표시, 음수는 '-'로 표시.
#진법에 맞게 숫자 앞에 표시한다. 0, 0x, 0X
0출력 대상 width의 빈 공간을 0으로 채운다.

폭(width)

  • 출력되는 데이터의 폭을 지정한다.
  • ex) 문자열 "abc"를 출력하기 위한 폭을 100으로 설정한다면, 100공간에 "abc"가 보여진다. (이 때 빈공간은 flag로 제어할 수 있다.)
  • width는 정수 값으로 입력받는다.
  • *로 입력된 경우는 반드시 인자로 정수를 함께 입력받아야하며, 입력값이 width로 설정된다.
    • *의 인자로 음수가 들어오는 경우 부호 -는 flag로 처리된다.
  int width = 10;
  printf("flag[*], width[%d] => [%*d]\n",width, width, 12345); // [     12345]

정밀도(precision)

  • 정밀도는 반드시 앞에 마침표(.)를 찍어야 한다. (폭과 구분하기위하여)
  • 출력 데이터의 정밀도를 지정한다. (쉽게 출력 할 자릿수를 지정한다.)
  • .마침표 뒤에 정수입력을 하지 않는 경우도 존재한다. (링크4 참조)
    • 이 경우 0을 출력한다고 했을 때, 정수%.d 와 실수%.f의 결과는 다르다.
      • 정수의 경우 아무것도 출력하지않는 반면, 실수는 [0]을 출력한다.
  • *로 입력되는 경우 인자로 정수를 함께 입력받고, 입력값이 precision으로 설정된다.
    • *의 인자로 음수가 들어오는 경우 정밀도는 0으로 처리된다.
    // 123
    printf("%10.3s\n","12345");
    // -00123
    printf("%10.5d\n", -123);
    // -123
    printf("% 10.1d\n", -123);
    // 123.1235
    printf("%10.4f\n", 123.123456789);
    
    int zeroI = 0;
    float zeroF = 0;
    // zeroI : [], zeroF : [0]
    printf("zeroI : [%.d], zeroF : [%.f]\n", zeroI, zeroF);

길이(length)

  • 출력할 데이터의 자료형 범위를 설정한다.

  • %d 서식문자의 경우 정수형 데이터를 10진법으로 출력 의 의미를 가진다. 여기에 길이를 지정해주면 출력할 데이터 자료형의 크기를 지정할 수 있다.

    길이d, io, u, x, Xf F e g G a Acspn
    defaultintunsigned intfloat, doubleintchar *void *int *
    hhsigned charunsigned charsigned char *
    hshort intunsigned short intshort int *
    llong intunsigned long intdoublewint_twchar_t *long int *
    lllong long intunsigned long long intlong long int *
    jintmax_tuintmax_tintmax_t *
    zsize_tsize_tsize_t *
    tptrdiff_tptrdiff_tptrdiff_t *
    Llong double

Step3 : 컴퓨터에서 실수를 표현하는 방식

참조

실수의 특징

  • 실수라는 수의 특징은 .(점)을 기준으로 정수와 실수를 구분한다.
  • 컴퓨터의 한정된 메모리 공간에서 실수를 해석하기 위해서는, 정수와 실수를 구분할 수 있어야 한다.

실수의 2진수 변환

  • 정수부는 10진수 변환과정과 동일하게 2로 나눈 나머지를 몫이 0이될 때까지 구한다.
  • 그리고 가장 마지막의 나머지부터 차례대로 나열하면 된다.
  • 실수는 실수부(소수점 아래)가 0이될 때까지 계속해서 2를 곱한다.
  • 0이될 때까지의 과정에서의 정수부(0 or 1)를 처음부터 차례대로 나열하면 된다.(정수는 마지막 부터 읽는다면, 실수는 처음부터 읽는다.)
    • ex) 12.125일 때
    • 정수부 => 1100
    • 실수부
      => 0.125 x 2 => 0.25
      => 0.25 x 2 => 0.5
      => 0.5 x 2 => 1.0
      => 따라서 실수부는 2진수로 001으로 표현.
    • 12.125 => 1100.001

고정 소수점방식?

  • 정수와 실수를 표현하는 비트수를 정해놓고 해석한다.
  • 만약 실수를 4byte공간에 저장할 때, 1bit = 부호, 16bit = 정수, 15bit는 실수를 표현한다고 가정한다면
  • 실수 12.125는 2진수로 1100.001이기 때문에 실수에 해당하는 2진수 100은 15비트 공간에 저장 된다. (뒷자리는 0으로 채움)
  • 고정 소수점 방식은 편리하기는 하지만, 정해진 비트의 범위가 상대적으로 적기 때문에 표현 가능한 정수의 범위가 적고, 실수를 표현할 때 정밀도또한 떨어지게 된다.
    • 만약 실수가 나누어 떨어지지 않는 경우에 실수를 2진수로 표현할 때 자리수가 계속해서 늘어나게 된다.
      • ex) 0.34를 2진수로 표현한다면 아래와 같이 연산이 계속 진행된다.
        => 0.34 x 2 => 0.68
        => 0.68 x 2 => 1.36
        => 0.36 x 2 => 0.72
        => 0.72 x 2 => 1.44
        => 0.44 x 2 => 1.88
        => ...
      • 위 경우, 고정 소수점방식에서는 실수 부를 최대 15bit로 표현하게 된다. 따라서 고정 소수점방식의 실수는 정밀도가 낮다. (부동소수점 방식에 비해)

부동 소수점방식?

  • 부동(floating)은 "둥둥 떠다니는"이라는 의미를 가지고있다.
  • 부동 소수점은 고정소수점과 반대로 소수점을 나타내는 "점"의 위치가 바뀐다는 특징을 가진다. (고정적이지 않다.)
  • 즉, 소수점의 위치가 동적이다.
  • 부동소수점 표현 방식은, 단정도(32bit)와 배정도(64bit)에 따라 실수를 표현하는 bit가 정해져 있고, 해석하는 방식이 정해져 있다.
  • 단정도와 배정도에따라 bit만 다를뿐 해석되는 의미는 동일하다.
  • 마지막 1bit는 부호비트이다.
  • 가수부를 나타내는 비트.
    • 쉽게, 실수를 2진수로 표현한 후 가수부에 저장한다.
    • 단정도는 8bit 배정도는 11bit로 표현한다.
  • 지수부를 나타내는 비트.
    • 쉽게, 가수부에서 2^n위치부터 실수임을 구분할 수 있다.
      • ex) 2^2라면 가수부의 n + 1비트부터는 실수(소수점 이하)를 나타낸다.
    • 가수부의 표현범위를 벗어난다면 bit수만큼 0으로 채워준다. (아래에서 추가설명 함)
  • 실수를 부동 소수점방식으로 표현한다면, 실수의 정밀도를 높이고 정수의 표현 범위도 넓힐 수 있다.
  • 부동 소수점 방식으로 표현하기 위해서는 2진수로 변환된 실수를 정해진비트에 저장하는 것이아니라, 정규화 과정을 통해 실수 및 정수의 표현범위를 넓힐 수 있다.
  • 쉽게 위에서 12.125의 2진수 1100.001을 1.100001 * 2^n으로 나타내도록 하는것이다.
    • 정확하게 얘기하면 정수부가 1만 남을때까지(중요) 소수점을 이동시킨다. (왼쪽 or 오른쪽) 그리고 이동한 칸 수만큼 n 자리에 집어 넣으면 된다.
    • 즉, 예시에서 n은 3이 된다.
    • 따라서 1.100001에서 2^3 이동한 후부터의 bit는 실수를 표현함을 구분할 수 있다.
      • 여기서 bit를 이동하여 실수를 구분한다고 하였다
      • 즉, 소수를 표현하는 bit의 공간이 고정적이지 않고 n의 크기에 따라 계속 변한다.
      • 소수표현을 위한 메모리 공간이 계속 변하기 때문에 floating(둥둥 떠다니는)것 같다는 표현을 하여 부동 소수점방식이라 표현한다.
    • 여기서 정규화 과정을 거쳐 만들어진 1.100001 * 2^n과 같은 표기법을 과학적 표기법이라고 한다.
    • 여기서 지수를 의미하는 n은 8bit공간에, 음수와 양수 모두 존재할 수 있다. (0.00012 같은 경우에는 1.2 * 10^-4 가 된다.)
    • 따라서 지수부에 값을 저장할 때는, bias값이라는 걸 더해주는데 4byte에선 127이된다.
    • 따라서 지수는 -127 ~ +128의 값을 가질 수 있고, 0~126은 음수 127은0 128~255은 양수 를 표현한다. (8byte에서 bias값은 1023)
    • 또한 정규화를 거쳐 저장 된 데이터는 아래와 같이 해석된다. (중요 !)
      • (+1) x 2^(130 - 127) x (1 + 2^-1 + 2^-6)
    • 만약 실수를 4byte공간에 저장할 때, 1bit = 부호, 8bit = n, 23bit는 이진수를 표현한다고 한다면?
      • 23bit공간에 이진수를 표현할 수 있다.
        • 정규화를 거쳐 만들어진 2진수는 위에서 설명했듯이 정수부를 1만 남기고 이동시킨다. 이 때 정수부는 항상 1이기 때문에 반드시 1.xxx ... 와 같은 형태이다.
        • 이 때 맨앞의 1은 생략하고 나머지를 23bit로 표현한다. 예시에서도 1.100001일 때 1을 제외한 100001 ... 이 채워진다.
        • 생략한 1을 숨겨진 비트(hidden bit)라고 한다. 실수 표현의 시작 bit는 1이 생략되있음을 절대로 망각하지 말자.
      • 8bit공간에는 실수 자료형이 표현된 비트를 구분할 수 있는 2^n의 값을 저장할 수 있다.
        • 여기서 의문점 1, 그렇다면 n비트 이후 부터 실수다 !를 구분할 수 있다면 n이 가수부의 23bit를 넘어가면 어떻게 될까?
        • 가수부의 범위를 넘어가는 경우, 23bit를 모두 정수로 해석한다. 또한 초과되는 bit만큼 0을 채워넣음으로써, 큰 범위의 정수를 표현한다.
        • 예를들어, 이진수가 1(hidden bit) 000 0000 0000 0000 0000 0001 일 때 지수부의 n이 30이라고 한다면?
        • 1(hidden bit) 000 0000 0000 0000 0000 0001 0000 00 과 같이 6bit가 0으로 채워짐으로써, 가수부에서 나타내는 정수가 더 큰 값을 가지고 있다는 것을 의미하게 된다.

Step4. 실수를 bit단위로 해석하기.

부동소수점 디버깅해보기

  • float타입의 10.0f는 어떻게 저장될까?
    • 32bit공간에 10.0을 표현한다.
    • 1bit는 부호비트, 8bit는 지수비트 , 나머지 23bit는 가수를 표현한다.
    • 예상한 값은 부호비트 = 0, 지수비트 = 0, 가수 = 10이 될것이라 예상했다.
    • 실제 메모리에 저장된 값 [ 00 00 20 41 ] 이다.
    • 이를 리틀엔디언 방식으로 해석하면 [ 41 20 00 00 ] 이다.
    • 2진수 표현으로 바꾸면? (4bit 2진수로 16진수 1개를 표현한다.)
      • [0100] [0001] [0010] [0000] [0000][0000][0000][0000]이 된다.
    • 부동소수점 표현방식에 맞게 해석하면 비트부호 = 0, 지수비트 = 10000010 , 가수비트는 010 0000 0000 ... 이 된다.
      • 이를 (-1)^0 x 2^(130 - 127) x (1 + 2^-2)로 해석할 수 있다.
      • 즉, 1 x 2^3 x 1 + 0.125 = 8 x 1.125 = 10.0이 된다.
    • 결론적으로, 저장된 bit를 해석하여 실수표현의 값을 유추할 수 있다.

bit연산 방법

  • 정리하면 Byte단위로 끊어서, 비트연산을 수행한다.
  • 위에서 10.0f가 메모리에 [00 00 20 41]과 같이 저장되어있을 때 리틀 엔디안 방식에 따라 해석하기위해 마지막 byte인 41부터 해석한다.
  • Byte단위로 해석하기 위해 float의 메모리 주소를 char *로 변환.
  • float(4byte)에서 마지막 byte의 시작은 시작주소 + 3byte이동으로 찾을 수 있다.
  • 해당 byte에 접근한 후, 1 (0000 0001) 과 비트연산 &를 수행한다.
  • [41]은 0100 0001이므로 (이해가 안된다면 참조 비트단위 연산 보기) 가장앞의 0100 0001부터 1과 비교하기위해 쉬프트 연산을 수행한다.
    • 즉, 처음에는 (char *로 변환 된 시작주소 + 3) >> 7 하면 0100 0001이 0000 0000이 되니깐 메모리의 0번째 bit를 맨 오른쪽으로 옮긴 후, 이 값이 1인지 0인지 알 수 있다.
    float d = 10.0f;

    unsigned char* ptr;
    ptr = (unsigned char*)&d;

    unsigned char dif = 128;
    int j = 0;
    for (int i = sizeof(float) - 1; i >= 0; i--) {
        for (j = 7; j >= 0; j--)
  	{
           // 8765 4321 이렇게 있으면 8을 1로보내서 1하고 & 연산 함.
            printf("%d", (*(ptr + i) >> j) & 0x01);
  	}
        printf(" ");
    }

Step5 : 구현하기

FlowChart

printf를 구성하기 위한 구조체 정의

typedef struct s_flag
{
	char plus;
	char minus;
	char space;
	char hash;
	char zero;
}				t_flag;
typedef struct s_input
{
	char	*str;
	char	sign;
	int		len;
}				t_input;
typedef struct	s_printf
{
	va_list	*ap;
	t_input	*input;
	t_flag	*flags;
	char	*length;
	char	specifier;
	int		width;
	int		precision_len;
}				t_printf;
  • s_printf
    • %이후에 나오는 printf의 옵션들을 저장.
  • s_input
    • 가변인자를 char *str에 저장, 부호 및 저장 된 str 크기를 기록
  • s_flag
    • printf에서 flag는 0개이상 존재할 수 있다.
    • 입력 된 모든 flag를 기록 후, write할 때 분기처리 한다.

고민한 점

flag가 0일 때, 정밀도가 존재한다면??

  • 정수의 경우
   	printf("%%010d :[%010d]\n", 12345); //[0000012345]
  	// ↓ warning: '0' flag ignored with precision and '%d' gnu_printf format occured 	
  	printf("%%010.1d :[%010.1d]\n", 12345); // [     12345]

16진수 음수 변환 ??

  • printf에서 음수의 16진수 변환은 제공하지 않는다.
  • man -3 printf => The unsigned int argument is converted to unsigned octal (o), unsigned decimal (u), or unsigned hexadecimal (x and X) notation.
  • 따라서 16진수로 표현되는 값은 0~ffffffff범위이다.
    • 여기서 ffffffff은 unsigned int 의 max값이다. => 4294967295
  • 예시
    • printf("%x", 0) => 0
    • printf("%x", -1) => ffffffff
    • printf("%x", -2) => fffffffe
    • printf("%x", -3) => fffffffd
    • printf("%x", UINT_MAX) => ffffffff
    • 따라서 -1은 unsigned int max와 같다.즉, 음수는 UINT_MAX + n + 1 (음수일 때) 과 같다.

실수처리...

  • 단순히 *10 , /10으로 소수점 자리수를 계산하면 유효자리가 커질수록 오차가 발생한다.
  • bit연산 방식에 대해, 다른 카뎃분께 설명들었는데.. 도저히 너무어려워서 오차를 최소한 하여 처리 함.
  • 입력 실수 n의 정수부는 n/10 >= 1 반복해서 구해서 double로 저장한다.
    • ex) 123.4567 이면 123.00000000이런식으로
  • 입력 실수 n의 실수부(소수점 이하)는 n - 위에서 구한 정수로 처리한다.
    • ex) 123.4567 이면 123.456700 - 123.000000 이런식으로..
  • 정밀도 + 1크기만큼 문자열로 만든다.
  • 문자열을 가지고 banker's rounding.

Makefile

  • libft.a를 내부적으로 사용하기 때문에, Recursive Make사용.
  • Makefile내부에서 다른 Makefile 실행 시키기. => 참조
  • but, re link가 안되고 계속 libftprintf.a가 ar되어서 그냥 libft파일도 다 명시함.

배운점

  • 부동소수점 저장방식.
  • printf 구현방식.

사용 Tester

  • pft_2019
    • printf소스가 있는 root에 clone해서, make re하면 됨.
    • root에는 내가 만든 make파일 존재해야 됨
  • pft
    • n, f, 길이 추가로 검사.(g, e는 구현 안함)
      • `./enable-test bonus && ./disable-test bonus_notrequired
      • ./disable-test "bonus*g"
      • ./disable-test "bonus*e"
  • printf_lover_v2
    • pft에 비해, 에러가 명시적이지 않음.
    • 결과 같은데 자꾸 틀렷다고하면 해당 test case에서 memory leak 체크해보기.

ETC

  • printf의 buffer기능에 대해 공부하기.
  • 자료구조, 컴퓨터구조, os, 네트워크 ,데이터베이스
profile
Bigmountain
:)
이전 포스트

Libft

다음 포스트

Get_Next_Line

0개의 댓글