최소 신장 트리
프림
크루스칼
비교
문제
프림 코드
크루스칼 코드
최소 신장 트리
무방향 그래프, 단방향 그래프에서 각 정점들을 최소값의 간선으로 연결 시켜 놓은 트리 형태로의 전환 알고리즘이다.
그림으로 쉽게 표현하면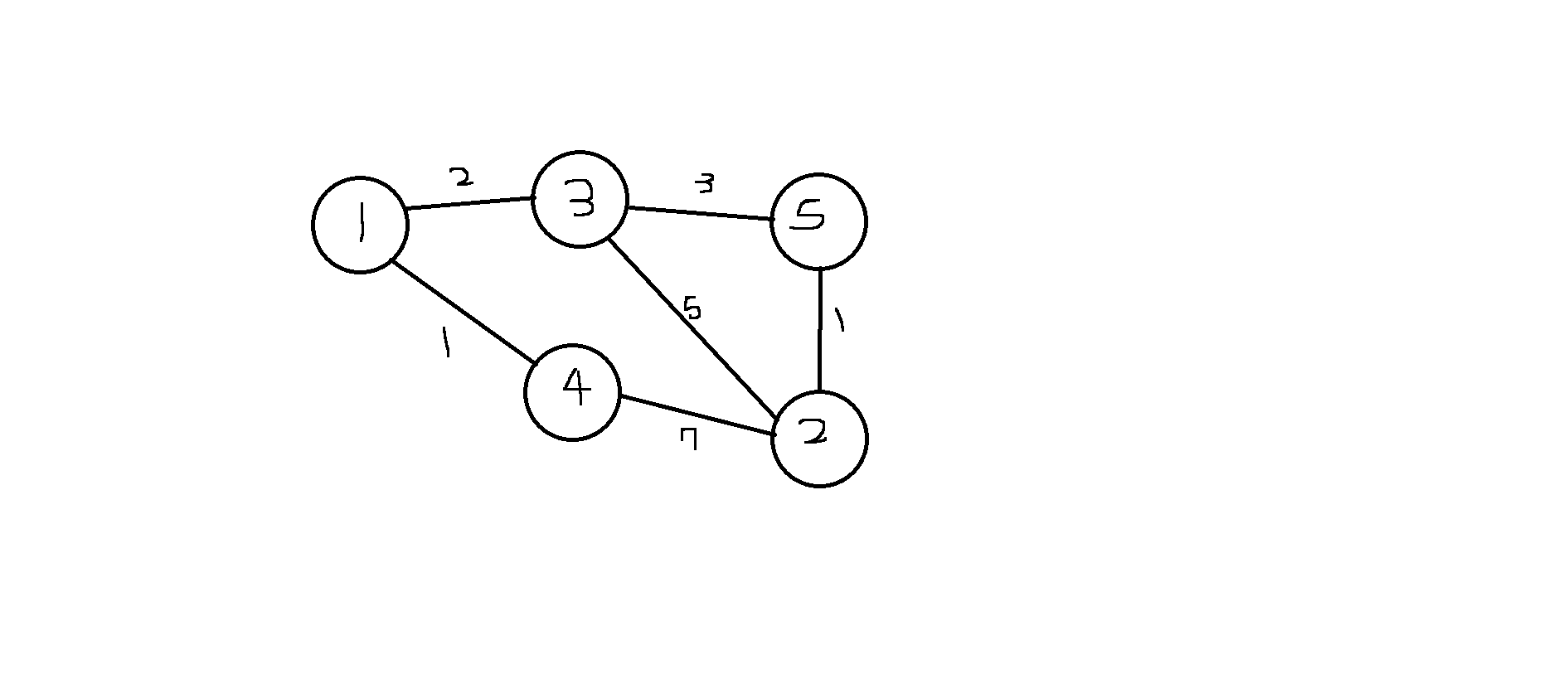
위와 같은 그래프에서 최소값의 간선으로만 표현하면
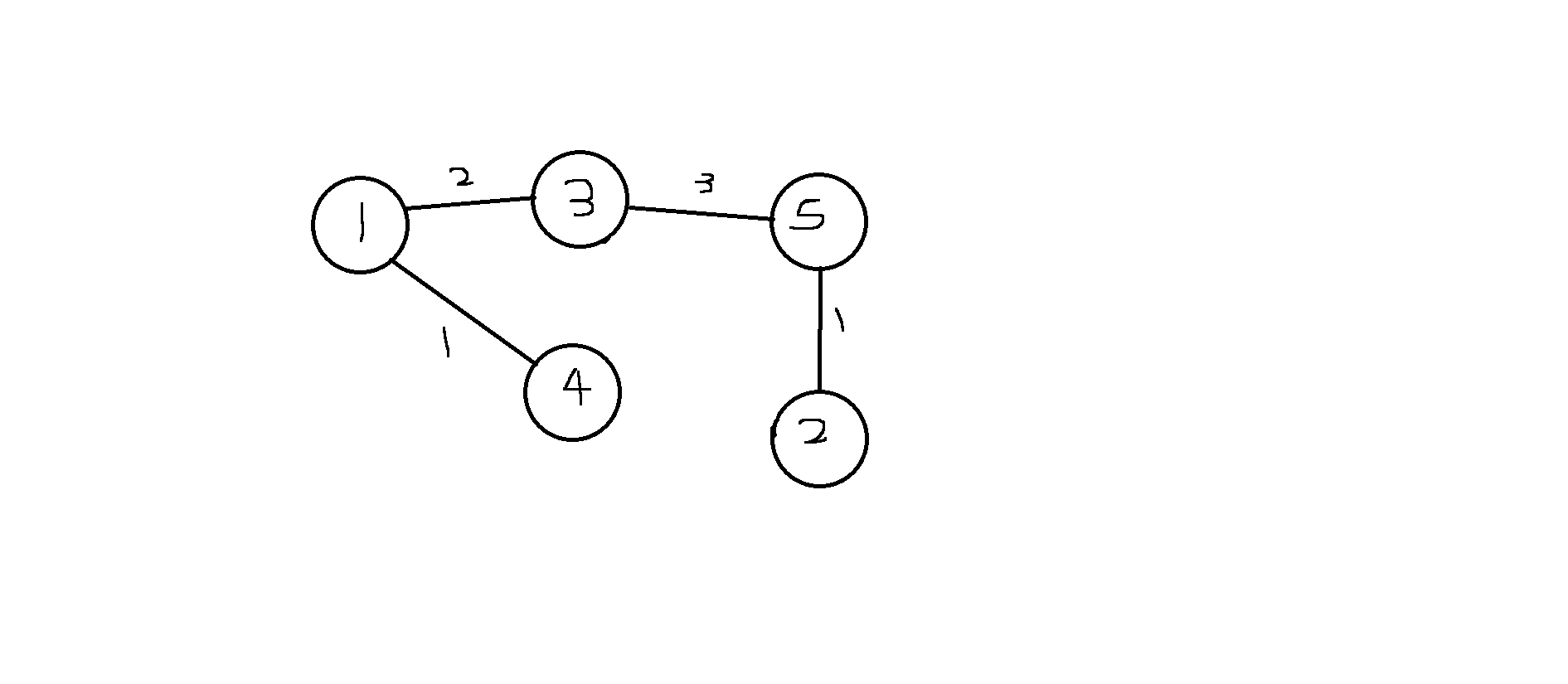
이렇게 모든 정점들은 연결되면서 최소값의 가중치로만 연결시켜놓는다.
최소 신장 트리를 만드는 방법은 두 가지 방법이 있다.
프림
프림은 최소 힙을 사용하여 MST를 구하는 방법이다.
1. 시작 지점 노드 필요
2. 해당 시작 지점에서 이동 할 수 있는 모든 노드들의 정보를 최소힙에 넣음
3. 방문한 곳은 다시 방문 하지 않음으로 사이클 방지
4. 최소힙에서 팝된 노드에서 다시 2번 반복
즉 시작 지점을 정하고 그 시작 지점에서 이동 할 수 있는 최소값의 가중치를 가진 노드를 선택하여 점진적으로 최소 신장 트리를 완성 시켜 나간다.
최소 힙을 사용하지 않으면 다음 노드를 탐색할때 방문 가능한 다음 노드들의 수 N x N만큼의 시간을 소모하여 최소값을 찾기 때문에 계속 추가되는 값들 중에서 최소값을 찾는 효율적인 방법인 최소힙을 사용하여 N log N으로 효율적이게 풀 수 있다.
그리디 알고리즘에서 최소값을 목표로 탐색하는 모습과 똑같다.
정점의 개수가 N
간선의 개수가 K
일 경우 시간복잡도는 K log N
크루스칼
크루스칼은 유니온 파인드를 사용하여 MST를 구하는 방법이다.
1. 가중치를 기준으로 주어진 간선들의 정보를 정렬
2. 정렬된 배열에서 작은 가중치부터 차례대로 사용
3. 유니온 파인드를 통해 배열에서 꺼내온 간선을 적용시키려 할때 사이클 여부 판단
4. 이미 방문한 정점 혹은 사이클 여부는 유니온 파인드를 통해서 거를 수 있음
프림과 달리 가중치를 기준으로 정렬된 배열의 맨 처음 간선 정보를 기준으로 시작하고 방문 여부와 사이클 여부를 유니온 파인드를 통해 판별하며 완성 시켜 나가는 방법이다.
간선 정렬을 선택했기 때문에 E log E 만큼의 시간에 다시 정렬된 배열을 순회하면서 유니온 파인드로 사이클여부를 판단하기 때문에 유니온파인드의 E log V만큼의 시간을 더한다
정점의 개수가 N
간선의 개수가 K
일 경우 시간복잡도는 K log N
비교
간선의 수가 많아질 경우 크루스칼은 모든 간선을 비교하여 정렬 후 진행하기 때문에 점진적으로 진행하며 간선의 최소값을 구하는 프림이 더 효율적 일 수 있다.
반면 간선의 수가 적다면 반대로 최소힙을 유지하는게 더 비효율적이고 모든 간선을 정렬 후 진행하는 크루스칼이 더 유리하다
정리
간선의 수가 많으면 : 프림
간선의 수가 적으면 : 크루스칼
구현 난이도 : 프림이 더 쉬움
문제
요약 : 정점 V와 간선 E가 주어지는데 E만큼의 간선 정보를 토대로 최소 신장 트리의 가중치를 구하라.
프림 코드
import sys, heapq
from collections import defaultdict
def s_input():
return sys.stdin.readline().strip()
min_heap = []
graph = defaultdict(dict)
visit = set()
V, E = list(map(int, s_input().split(" ")))
for _ in range(E):
src, dst, w = list(map(int, s_input().split(" ")))
graph[src][dst] = w
graph[dst][src] = w
result = 0
heapq.heappush(min_heap, (0, 1))
past_node = 1
while min_heap:
cur_v, cur_node = heapq.heappop(min_heap)
if cur_node in visit:
continue
past_node = cur_node
visit.add(cur_node)
result += cur_v
for next in graph[cur_node].keys():
heapq.heappush(min_heap, (graph[cur_node][next], next))
del mst_graph[1][1]
print(result)크루스칼 코드
import sys, heapq
from collections import defaultdict
def s_input():
return sys.stdin.readline().strip()
def find_parent(graph, a):
parent = a
while graph[parent] != parent:
parent = graph[parent]
return parent
def union(graph, a, b):
a_parent = find_parent(graph, a)
b_parent = find_parent(graph, b)
if a_parent < b_parent:
graph[b_parent] = a_parent
elif a_parent > b_parent:
graph[a_parent] = b_parent
def has_cycle(graph, a, b):
return find_parent(graph, a) == find_parent(graph, b)
min_heap = []
graph = []
union_graph = {}
mst_graph = defaultdict(dict)
V, E = list(map(int, s_input().split(" ")))
for i in range(1, V + 1, 1):
union_graph[i] = i
for _ in range(E):
src, dst, w = list(map(int, s_input().split(" ")))
edge = {src : {dst : w}}
graph.append(edge)
graph.sort(key=lambda x : list(list(x.values())[0].values())[0])
connected_vertex = 0
result = 0
for i in range(E):
if connected_vertex == V:
break
src = list(graph[i].keys())[0]
dst = list(graph[i][src].keys())[0]
w = graph[i][src][dst]
if has_cycle(union_graph, src, dst):
continue
union(union_graph, src, dst)
mst_graph[src][dst] = w
mst_graph[dst][src] = w
result += w
connected_vertex += 1
# print(mst_graph)
print(result)